88-341 תשעג סמסטר א/תרגילים/תרגיל 7
שאלה 1
השאלה הזו לוקחת אותנו קצת אחורה בחומר, אבל היא חשובה מאוד.
תהי 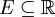 . הוכיחו כי התנאים הבאים שקולים:
. הוכיחו כי התנאים הבאים שקולים:
(1)  מדידה לבג.
מדידה לבג.
(2) לכל  קיימת קבוצה
קיימת קבוצה 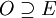 , פתוחה ב-
, פתוחה ב-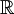 , עבורה
, עבורה 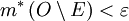
(3) לכל  קיימת קבוצה
קיימת קבוצה 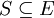 , סגורה ב-
, סגורה ב-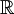 , עבורה
, עבורה 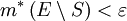
(4) קיימת קבוצה 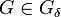 , כך ש-
, כך ש-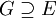 , וגם
, וגם 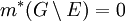
(5) קיימת קבוצה 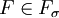 , כך ש-
, כך ש-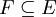 וגם
וגם 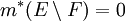
הדרכה:
א. הניחו תחילה כי 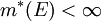 , והוכיחו
, והוכיחו 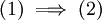
ב. ע"פ א' הראו כי לכל קבוצה  מתקיים
מתקיים 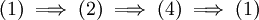 (אפילו אם
(אפילו אם 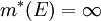 ).
).
בשביל להראות 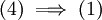 כדאי לזכור שקבוצות מטיפוס
כדאי לזכור שקבוצות מטיפוס 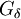 הן מדידות לבג (וגם כמובן קבוצות עם מידת לבג חיצונית 0).
הן מדידות לבג (וגם כמובן קבוצות עם מידת לבג חיצונית 0).
ג. ע"פ ב' הראו כי לכל קבוצה  מתקיים
מתקיים 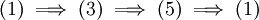 .
.
בשביל הגרירה 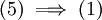 כדאי לזכור שקבוצות מטיפוס
כדאי לזכור שקבוצות מטיפוס 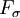 מדידות לבג (ושוב, כמובן שגם קבוצות עם מידת לבג חיצונית 0).
מדידות לבג (ושוב, כמובן שגם קבוצות עם מידת לבג חיצונית 0).
שאלה 2
א. בתרגול הראינו שאם ![I=[a,b]](/images/math/a/a/9/aa922a30ce1173792a5bbaaeec5dd22c.png) קטע סגור וחסום, אזי מרחב הפונקציות הרציפות בו בהחלט,
קטע סגור וחסום, אזי מרחב הפונקציות הרציפות בו בהחלט, ![\text{AC} \left( \left[ a,b \right] \right)](/images/math/c/8/e/c8e9bd6961aaae0601374a502d4c364f.png) , סגור ביחס לכפל בסקלר, חיבור פונקציות וכפל פונקציות.
, סגור ביחס לכפל בסקלר, חיבור פונקציות וכפל פונקציות.
מה ניתן לומר על המרחב 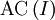 אם
אם 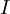 קטע לא חסום? הוכיחו את דבריכם!
קטע לא חסום? הוכיחו את דבריכם!
ב. יהי 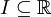 קטע כלשהו,
קטע כלשהו, 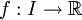 ממחלקה
ממחלקה 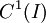 (גזירה ברציפות בקטע). האם
(גזירה ברציפות בקטע). האם 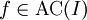 ?
?
ג. הוכיחו ע"י שלילת ההגדרה (ורק ע"י שלילת ההגדרה!) כי פונקציות קנטור אינה רציפה בהחלט בקטע ![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) .
.
רמז: אם בוחרים את הקטעים 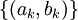 בחכמה, זה פשוט.
בחכמה, זה פשוט.
שאלה 3
כזכור אם  פונקציה ממשית, ומוגדרת בסביבת הנקודה
פונקציה ממשית, ומוגדרת בסביבת הנקודה  , הנגזרת הסימטרית שלה שם מוגדרת ע"י
, הנגזרת הסימטרית שלה שם מוגדרת ע"י 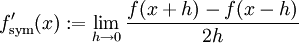 (אם הגבול קיים כמובן).
(אם הגבול קיים כמובן).
א. הוכיחו כי אם  גזירה בנקודה כלשהי
גזירה בנקודה כלשהי 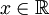 , אזי הנגזרת הסימטרית קיימת בנקודה זו, ומתקיים
, אזי הנגזרת הסימטרית קיימת בנקודה זו, ומתקיים 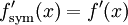 .
.
ב. תנו דוגמא למצב שבו  לא גזירה בנקודה כלשהי
לא גזירה בנקודה כלשהי  - ובכל זאת קיימת
- ובכל זאת קיימת 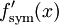 .
.
בהצלחה!
זוהי עוד לא גרסה סופית של השאלות!