תוכן עניינים

הוספת שאלה חדשה

הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).

-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן

אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.

1. מה צריך לקיים חסם עליון של קבוצה, שהוא גם המקסימום של הקבוצה?

2. נניח שנתונה הקבוצה הבאה:

 zz A={2,3,5,8} zz

החסם העליון שלה הוא 8.

אבל משהו כאן לא ברור לי.

ע"פ הגדרת החסם העליון מתקיים ש-8 חסם מלעיל של A (עם הדרישה הזו אין לי בעיה).

אבל צריכה להתקיים דרישה נוספת, שאיתה דווקא יש בעיה...

הדרישה אומרת שלכל e>0 קיים איבר a ב-A כך ש-a > 8-e.

אבל עבור e=0.1 למשל, (ועבור אפסילונים רבים אחרים), לא קיים איבר a ב-A כך ש- a>8-e.

אם כך, הדרישה השנייה של קיום חסם עליון, אינה מתקיימת. מדוע אז 8 הוא בכל זאת חסם עליון?

על מנת להיות מקסימום, האיבר צריך להיות שייך לקבוצה. לגבי הדוגמא שנתת, בוודאי שיש איבר a כזה. שכחת את 8 בעצמו! הרי

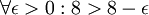
\forall \epsilon>0:8>8-\epsilon

--ארז שיינר 21:31, 23 באוקטובר 2013 (IDT)

תודה

אומנם מופיע גם הפתרון..אבל יש שם כמה דברים שלא מובנים לי..

השאלה הולכת כך:

יהיו קבוצות A,B מוכלות בממשיים. כל איבר ב-A קטן או שווה לכל איבר ב-B.

צריך להוכיח ש-supA<=infB.

האמת שזה די אינטואיטיבי..במיוחד אם מסתכלים על שניי תת-קטעים A , B , על הציר הממשי, שמקיימים את הנתון שכל איבר ב-A קטן שווה לכל אביר ב-B.

בסדר..מניחים בשלילה ש-supA>infB

האם נכון לומר, שמההנחה בשלילה אפשר להסיק שיש קטע (infB,supA), כך שכל איבר בקטע שייך גם לקבוצה A וגם לקבוצה B?

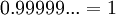
זה הוזכר גם בהרצאה וגם בתרגול ולא מובן לי בכלל למה זה נכון.