88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 11
הגדרות בסיסיות
הגדרה יהיה  קבוצה לא ריקה. יהא
קבוצה לא ריקה. יהא  קבוצה המכילה זוגות לא סדורים מאיברי
קבוצה המכילה זוגות לא סדורים מאיברי  אזי
אזי  נקרא גרף לא מכוון.
נקרא גרף לא מכוון.
חושבים על  כקודקודים של הגרף ועל
כקודקודים של הגרף ועל  כקשתות/צלעות של הגרף. את האיברים ב
כקשתות/צלעות של הגרף. את האיברים ב  נהוג לרשום כקבוצה
נהוג לרשום כקבוצה 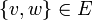 (בגלל שזה זוגות לא סדורים)
(בגלל שזה זוגות לא סדורים)
דוגמא: 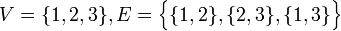 מייצג משולש.
מייצג משולש.
הגדרה הסדר של גרף  הוא
הוא 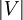 . גרף יקרא סופי אם הסדר שלו סופי (וגם
. גרף יקרא סופי אם הסדר שלו סופי (וגם  סופית)
סופית)
אנחנו נעסוק בגרפים לא מכוונים בלי לולאות כלומר המקיימים 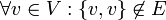
הגדרה יהיה  נאמר כי
נאמר כי 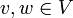 שכנים אם
שכנים אם 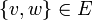 .
.
במקרה זה נאמר כי הצלע 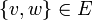 חלה ב
חלה ב 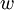 (או חלה ב
(או חלה ב 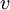 )
)
את קבוצת השכנים של 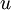 מסמנים כ
מסמנים כ 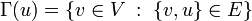
הדרגה של 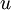 (סימון:
(סימון: 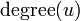 )היא מספר הצלעות החלות ב
)היא מספר הצלעות החלות ב 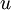 או לחילופין
או לחילופין 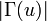
בדוגמא של המשולש - כל 2 קודקודים שכנים. כל קודקוד מדרגה 2. השכנים של קודקוד מספר 1 הוא קודקוד 2 + קודקוד 3.
משפט (לחיצת הידיים)
יהי  גרף לא מכוון. אזי
גרף לא מכוון. אזי 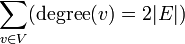 .
.
עוד הגדרות:
יהי  גרף לא מכוון. סדרת קודקודים (סדורה)
גרף לא מכוון. סדרת קודקודים (סדורה) 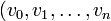 נקראת מסלול אם
נקראת מסלול אם
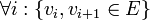
מסלול יקרא פשוט אם כל הקודקודים 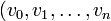 שונים זה מזה
שונים זה מזה
מעגל הוא מסלול המקיים 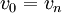
מעגל פשוט מסלול שכל קודקודיו שונים פרט לקודקוד הראשון והאחרון ששווים (כלומר 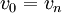 )
)
אורך המסלול 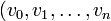 הוא
הוא 
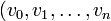 הינו מסלול מ
הינו מסלול מ 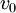 ל
ל 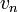
הגדרה
המרחק בין 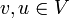 הוא המסלול עם אורך מינמאלי בין הקודקודים. (סימון
הוא המסלול עם אורך מינמאלי בין הקודקודים. (סימון 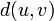 או
או 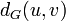 ).
).
אם אין מסלול בין 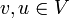 נסמן
נסמן 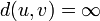
הקוטר של גרף  מוגדר כמרחק המקסימאלי בין 2 קודקודים . כלומר
מוגדר כמרחק המקסימאלי בין 2 קודקודים . כלומר 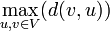
בניה
עבור גרף לא מכוון  נגדיר יחס שקילות
נגדיר יחס שקילות 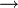 על
על  כך:
כך:
לכל 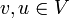 מתקיים
מתקיים 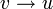 אמ"מ קיים מסלול מ
אמ"מ קיים מסלול מ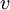 ל
ל 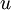 (כלומר
(כלומר 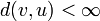 )
)