לינארית 1 לתיכוניסטים תש"ע - שאלות ותשובות
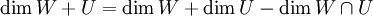
תוכן עניינים
הוראות
כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחילת הדף את השורה הבאה:
== כותרת לשאלה ==
לכתוב מתחתיה את שאלתכם, וללחוץ על שמירה למטה מימין
הודעה חשובה !!! - יש להגיש את התרגילים הנוספים (13 , ו 14 כרשות למי שמגיש ) עד ,וכולל , 16.9.2010 ! למשל לתא הבודקת הילה הלוי בכר , או לתומר ביום רביעי או לניר ביום חמישי - בתרגולי החזרה . אנא הודיעו למי שאתם יודעים שלא יגיע לתרגולים אלו . תודה:)
ארכיון
ארכיון 1 - תרגיל 1
ארכיון 2 - תרגיל 2
שאלות
מרוכבים בבוחן
שלום רב, האם תתכן משוואה מרוכבת כפי שנתנה בדף התרגול בבוחן עצמו? אם כן, מכיוון שאסור שימוש במחשבון, עלינו ללמוד את ערכי הסינוס, קוסינוס וטנגנס של זוויות נפוצות (30, 45, 60, 120, ... ואם כן אז אילו זוויות נפוצות?) או שבמידה ונשאל את הבוחן ייאמר לנו? תודה מראש.
הוכחה שיש איבר הופכי בשדה 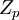
ההוכחה מורכבת משלב א' בו מוכיחים שאם 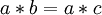 כאשר
כאשר 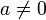 אז
אז 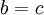 .
.
בשלב השני, אומרים שיש 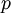 איברים שונים בקבוצה
איברים שונים בקבוצה 
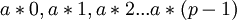 כאשר
כאשר 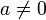 , וגם P איברים ב-
, וגם P איברים ב-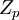 , לכן כל האיברים ב-
, לכן כל האיברים ב-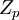 נמצאים ב-
נמצאים ב- כולל
כולל 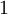 . כלומר קיים
. כלומר קיים 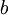 ב-
ב-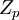 כך ש-
כך ש-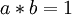 .
.
אז לא הבנתי:
1. למה שלב א' לא מספיק בשביל להוכיח שיש איבר הופכי? בשביל מה שלב ב'?
הרי אם הוכחנו את שלב א', זה אומר שיש איבר 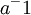 כך ש-
כך ש- . כלומר יש איבר הופכי ל-
. כלומר יש איבר הופכי ל- .
.
2. האם שלב ב' לא מספיק, בלי שלב א' בשביל להוכיח שיש הופכי? הרי הוכחנו שקיים 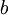 כך ש-
כך ש-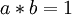 , כלומר קיים איבר הופכי ל-
, כלומר קיים איבר הופכי ל- .
.
בקיצור לי נראה כאילו שלב א' ושלב ב' מספיקים כל אחד מהם בשביל להוכיח שיש הופכי.
אפשר הסבר? תודה.
תשובה
שלב א לא מספיק מהסיבה הפשוטה ש (הדבר תקף לכל שדה ולא רק לשדה 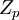 כלשהו):
יהי
כלשהו):
יהי 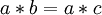 ומכאן ש -
ומכאן ש - 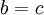 . אבל שים לב שלא רשום לנו בהכרח
. אבל שים לב שלא רשום לנו בהכרח 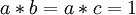 , ולכן קיימת דוגמה נגדית לכך ש- c ו- b אינם ההופכיים של a, למשל
, ולכן קיימת דוגמה נגדית לכך ש- c ו- b אינם ההופכיים של a, למשל 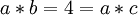 . במקרה זה אכן מתקיים ש-
. במקרה זה אכן מתקיים ש-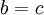 אבל לא מתקיים שהם ההופכיים של a.
אבל לא מתקיים שהם ההופכיים של a.
שלב ב לא מספיק מהסיבה הפשוטה ש:
הוכחת ש-1 נמצא ב-  ועפ"י הגדרת הקבוצה
ועפ"י הגדרת הקבוצה  שנתת יתקיים ש:
שנתת יתקיים ש: 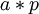 גם הוא איבר של
גם הוא איבר של  .
יהיו p, t איברים שונים בהם מכפילים את a ומקבלים 1. עפ"י שלב א הוכחת ש-p=t וזוהי סתירה כמובן. ולכן לכל a מ-
.
יהיו p, t איברים שונים בהם מכפילים את a ומקבלים 1. עפ"י שלב א הוכחת ש-p=t וזוהי סתירה כמובן. ולכן לכל a מ-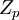 איבר הופכי אחד בלבד, דבר המקיים את תכונת ההופכי.
איבר הופכי אחד בלבד, דבר המקיים את תכונת ההופכי.
שים לב שאם מבקשים ממך להוכיח ש- 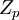 מסוים הוא שדה אז ניתן להוכיח את תכונת האיברים ההופכיים ע"י לוח הכפל של השדה המסוים שעבורו התבקשת להוכיח (או להפריך אותה עבור p שאינו ראשוני).
מסוים הוא שדה אז ניתן להוכיח את תכונת האיברים ההופכיים ע"י לוח הכפל של השדה המסוים שעבורו התבקשת להוכיח (או להפריך אותה עבור p שאינו ראשוני).
מקווה שעזרתי, גל.
שאלה
האם מישהו יכול להגיד מה מבנה הבוחן וכמה זמן יש לנו?
תשובה
3 שאלות מתוך 4, 45 דקות.