שיחה:88-222 תשעד סמסטר ב מגרל
מתוך Math-Wiki
תוכן עניינים
הוספת שאלה חדשה
הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).
-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן
אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.
שאלות
הוכחת טענה מהתרגול
בתרגול השלישי נאמר ש- U פתוחה ב-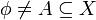 אם ורק אם קיימת V פתוחה ב-X כך ש-
אם ורק אם קיימת V פתוחה ב-X כך ש- 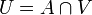 .
אפשר בבקשה עזרה בהוכחה מימין לשמאל (אם U פתוחה אז קיימת V...) ?
.
אפשר בבקשה עזרה בהוכחה מימין לשמאל (אם U פתוחה אז קיימת V...) ?
- (לא מרצה / מתרגל) תהי קבוצה פתוחה
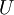 . לפי ההגדרה, לכל
. לפי ההגדרה, לכל 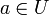 קיים
קיים 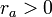 שעבורו
שעבורו 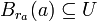 . ניקח את איחוד כל הכדורים האלו, זאת אומרת את
. ניקח את איחוד כל הכדורים האלו, זאת אומרת את 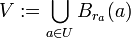 . לפי תכונות שהוכחו, זו קבוצה פתוחה ב-
. לפי תכונות שהוכחו, זו קבוצה פתוחה ב-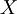 , ואכן מתקיים
, ואכן מתקיים 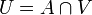 ; ההכלה משמאל לימין ברורה, וההכלה מימין לשמאל נובעת מכך שאם
; ההכלה משמאל לימין ברורה, וההכלה מימין לשמאל נובעת מכך שאם 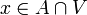 , בהכרח
, בהכרח 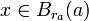 כלשהו וגם
כלשהו וגם 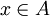 , ולכן, לפי הבחירה של
, ולכן, לפי הבחירה של 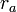 ,
, 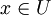 --גיא בלשר (שיחה) 04:24, 4 באפריל 2014 (EDT)
--גיא בלשר (שיחה) 04:24, 4 באפריל 2014 (EDT)
תרגיל 4 שאלה 1
אני מצרף ניסיון הוכחה נוסף לטענה 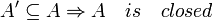 , אשמח אם לדעת האם הוא נכון.
, אשמח אם לדעת האם הוא נכון.
תהי 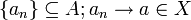 . אם היא קבועה לבסוף אז ודאי שהגבול בA. אחרת, יש תת סדרה
. אם היא קבועה לבסוף אז ודאי שהגבול בA. אחרת, יש תת סדרה 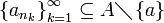 . כל תת סדרה של מתכנסת תתכנס גם היא ולאותו גבול, לכן לפי הגדרה
. כל תת סדרה של מתכנסת תתכנס גם היא ולאותו גבול, לכן לפי הגדרה 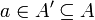 , לכן
, לכן  .
.
 ולכן כאשר אתה אומר לכל
ולכן כאשר אתה אומר לכל 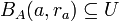 . בעוד ש
. בעוד ש 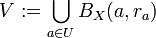 כלומר איחוד כדורים פתוחים ב
כלומר איחוד כדורים פתוחים ב