לינארית 2 לתיכוניסטים תש"ע
תוכן עניינים
- 1 הוראות
- 2 ארכיון
- 3 שאלות
- 3.1 שאלה בקשר לבוחן
- 3.2 שאלה חשובה לדוגמא
- 3.3 שאלה לארז
- 3.4 תרגיל 1.4
- 3.5 תרגיל 1.9
- 3.6 שאלה
- 3.7 שאלה
- 3.8 שאלה
- 3.9 שאלה 4.12.0.5
- 3.10 לארז - בקשר לשאלת הבונוס שנתת בכיתה
- 3.11 שאלה 5.7
- 3.12 שאלה
- 3.13 שאלה - 5.10
- 3.14 שאלה 5.14
- 3.15 שאלת בונוס
- 3.16 אי שיוויון בסל
- 3.17 בנוגע לתרגיל הנוסף
- 3.18 שאלה
- 3.19 שאלה 2 תרגיל 7
- 3.20 שאלה
- 3.21 שאלה
- 3.22 מספר שאלות די בסיסיות בנושאים שונים
- 3.23 שאלות :)
- 3.24 שאלה
- 3.25 שאלה בקשר למטריצת גראם
- 3.26 שאלה
- 3.27 שאלה
- 3.28 שאלה
- 3.29 שאלה
- 3.30 שאלה 2
- 3.31 שאלה 1 ב
- 3.32 שאלה קטנה (בנוגע לכתיבה)
- 3.33 שאלה 1 סעיף ב
- 3.34 שאלה - בנוגע לשאלה 4
- 3.35 שאלת קידבק
- 3.36 שאלה בקשר ללכסון
- 3.37 שאלה
- 3.38 שאלה
- 3.39 שאלה
- 3.40 שאלה בקשר לבוחן
- 3.41 שאלה: תרגיל 8.
הוראות
כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחתית הדף את השורה הבאה:
== כותרת שאלה ==
לכתוב מתחתיה את השאלה שלכם, וללחוץ על 'שמירה'.
(אין צורך להרשם לאתר. רק לעקוב אחרי ההוראות הפשוטות...)
ארכיון
ארכיון 1 - שאלות על תרגילים 1-4
שאלות
שאלה בקשר לבוחן
היי ארז. אתה יכול בבקשה להעלות רשימה מדוייקת של הנושאים שיש לבוחן? ואתה יכול בבקשה להעלות גם תרגילי הכנה? תודה.
שאלה חשובה לדוגמא
מה זה Span?
תשובה
אוסף כל הצירופים הלינאריים
--ארז שיינר 20:07, 22 באוקטובר 2009 (UTC)
- הבנתי, תודה.
- בשמחה
- יותר קונסטרוקטיבי לחשוב על זה כ"המרחב הנפרש", התת-מרחב הקטן ביותר שמכיל את הקבוצה הנתונה.
שאלה לארז
האם קיימת אפשרות לשמור את כל התוכן של דף זה בדף אחר (שאלות ותשובות 1 - תרגילים 1-4, למשל..), ולמחוק את כל מה שיש כרגע פרט לשאלות שרלוונטיות לתרגיל ולחומר של השבוע, במטרה להקל על הצפייה והטעינה?
תשובה
כן, אני אעשה את זה. אני מבקש לא למחוק שום דבר שנרשם אף פעם משום סיבה, אלא אם אתם בעצמכם כתבתם את זה.
תרגיל 1.4
בסעיפים ב' וג' יש הפניה לשאלה 1.1, ואני לא ממש מצליחה למצוא ת'קשר... יש בעיה עם ההבנה שלי או עם הספר??
תשובה
הכוונה לשאלה 1.3 לשני הסעיפים
- העתקתי את השאלה מהארכיון כיון שהיא קשורה לתרגיל של השבוע הזה.
תרגיל 1.9
האם שתי המכפלות הן אותן מכפלות? (בסעיף א'..) או שבג' מתעלמים מסעיף א'? כלומר הנתון היחיד שלי זה 2 התכונות בסעיף ב' ואני צריכה להוכיח שהמכפלה שמוגדרת בסעיף ג' היא למעשה לא מכפלה פנימית?
תשובה
בסעיף א' נאמר שכל מכפלה פנימית מקיימת את התכונה 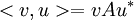 . בסעיף ג', צריך להראות שיש מטריצות שעונות על התכונות בסעיף ב' אך עדיין אין מכפלה פנימית שיוצרת אותן כמו בסעיף א'. אם הייתה מכפלה כזו, אז היא הייתה מקיימת את השיוויון
. בסעיף ג', צריך להראות שיש מטריצות שעונות על התכונות בסעיף ב' אך עדיין אין מכפלה פנימית שיוצרת אותן כמו בסעיף א'. אם הייתה מכפלה כזו, אז היא הייתה מקיימת את השיוויון 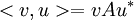 , ולכן הפונקציה הזו הייתה אכן מכפלה פנימית.
, ולכן הפונקציה הזו הייתה אכן מכפלה פנימית.
שאלה
יש להביא דוגמא נגדית ב 1.5?
תשובה
יש להראות שאחד מחוקי המכפלה הפנימית לא מתקיים. אפשר לעשות את זה על ידי דוגמא נגדית לחוק שלא מתקיים בעזרת מספרים מרוכבים
שאלה
ארז - האם קיים חוק שאומר : לכל v שונה מאפס מתקיים ש: <v,v> גדול מאפס? (גדול ממש)
תשובה
כן, חוק אי שליליות אומר ש 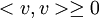 ושיוויון מתקיים
ושיוויון מתקיים 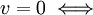 . במילים אחרות, אם
. במילים אחרות, אם 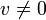 אזי
אזי 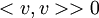 ממש
ממש
שאלה
האם מותר לי להשתמש בשעורי הבית בכל המשפטים שנלמדו בהרצאה? (בהנחה שלא מבקשים להוכיח אותם)
תשובה
עקרונית כן, אבל זו שאלה דיי כללית
שאלה 4.12.0.5
האם מתכוונים בשאלה להוכחה רק לגבי המכפלה הפניימית הסטנדרטית או לכל מכפלה פנימית?
תשובה
המכפלה הפנימית הסטנדרטית, אבל שים לב שזו הסטנדרטית מעל 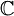 , כלומר
, כלומר 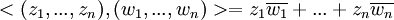
- בסדר אבל אני לא מתייחס כל כך בהוכחה שזה C כי זה נכון גם ל C וגם לr ההוכחה שלי
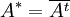 , איך אפשר לא להתייחס למרוכבים כשמדובר על הצמדה?
, איך אפשר לא להתייחס למרוכבים כשמדובר על הצמדה?
לארז - בקשר לשאלת הבונוס שנתת בכיתה
כל הדרך הביתה ישבתי על ההוכחה, אח"כ ישבתי כמעט כל הלילה בשביל הבונוס הזה. בסה"כ ישנתי קצת פחות מ-4 שעות. האם אתה יכול לומר לנו סוף סוף אם מישהו הצליח להוכיח, אם קבלת, ואם מישהו כבר קבלת את הבונוס?
תשובה
יש כבר פותרים, אני אפרסם את הפתרונות בקרוב, אני עוד עובר על הוכחות.
שאלה 5.7
ניסיתי לחלק ל-3 מקרים אבל לא ממש יצא לי.. אפשר איזשהו רמז?
תשובה
אילו מקרים? מה התנאי למרחב ניצב? תבדוק אותו מפורשות
שאלה
האם מותר בשאלה זו (5.7) להשלים את הקבוצה S לבסיס אורתונורמלי, לפי המשפט שאומר שכל קבוצה אורתונורמלית ניתנת להשלמה לבסיס אורתונורמלי?
תשובה
זה מותר ונכון אבל אין צורך בזה, התשובה פשוטה יותר. כמו שרשמתי למעלה, צריך לבדוק את התנאי לניצבות, וזו תשובה של שתי שורות.
בתגובה לתשובה
תודה רבה. לא הצלחתי לעלות על התשובה, אז ספקתי תשובה די ארוכה של עמוד שלם של הוכחה, למרות שהוכחה הייתה מאוד קלה.
שאלה - 5.10
האם קיימת סיבה לכך שההדרכה אומרת לבחור בסיס, ורק אח"כ לבצע גרם-שמידט? האם לא יכלנו לבחור מראש בסיס אורתונורמלי? דבר נוסף, רק לשם בדיקה: האם גם לכם ייצא שהמכפלה הפנימית: <v,w> שווה לאלפא-i בריבוע?
תשובה
אתה צודק אפשר לקחת ישר בסיס אורתונורמלי, אבל חשוב מאד לקחת בסיס לU ולהשלים אותו להיות בסיס למרחב כולו.
שאלה 5.14
איך מוצאים בסיס ומימד למרחב הניצב רק ע"י span של המרחב?
תשובה
אם וקטור הוא אורתוגונלי לבסיס של הspan, מה המכפלה הפנימית שלו עם שאר איברי הspan?
ושאלה נוספת, למה שווה הסכום 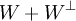 ?
?
--ארז שיינר 19:45, 26 בנובמבר 2009 (UTC)
- אני יכולה בעצם לומר: כדי שוקטור יהיה בW+, הוא צריך לקיים שהמכפלה הפנימית שלו עם 2 הוקטורים הנתונים הם 0.. ואז להגדיר V =(x,y,z) ולמצוא לאיזה ערכים של x,y,z שמובעים לדוגמה באמצעות Z זה מתקיים? ומשם גם להוציא את הבסיס..?
- כן. וההסבר לכך הוא מה שרשמתי למעלה (זה לגבי מציאת הבסיס, ולא לגבי המימד. את המימד ניתן לומר מיד).
שאלת בונוס
לגבי ההוכחה הראשונה שניתנה.. למה מותר להניח שבפולינום האופייני של A^2 - המעלה הגבוהה ביותר של (x-alpha)לע"ע alpha כלשהו היא 1?
תשובה
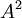 לכסינה. לפי התיקון השני לתרגיל, הפולינום האופייני שלה מכיל גורמים לינאריים בלבד. (אחרת היה בלוק ז'ורדן בגודל גדול מ1 ואז צורת הז'ורדן לא הייתה אלכסונית).
לכסינה. לפי התיקון השני לתרגיל, הפולינום האופייני שלה מכיל גורמים לינאריים בלבד. (אחרת היה בלוק ז'ורדן בגודל גדול מ1 ואז צורת הז'ורדן לא הייתה אלכסונית).
- נכון, אבל למה זה אומר שלא יכול להיות (x-alpha)^3 למשל..? זה מתפרק ל(x-alpha)(x-alpha)(x-alpha(
- עשיתי שני בלבולים:
- מדובר על הפולינום המינימלי ולא האופייני של
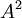
- התיקון השני אמר שהחזקה של הגורמים הלינאריים בפולינום המינימלי חייבת להיות אחד. הסיבה לפי צורת ז'ורדן היא כפי שרשמתי למעלה, כי גודל הבלוק המקסימלי הוא בגודל חזקת הגורם הלינארי בפולינום המינימלי.
אי שיוויון בסל
ניסיתי להוכיח בבית ששיוויון מתקיים אם ורק אם v שייך לspan{v1,..vk} אבל הצלחתי להוכיח רק את הכיוון <==. אפשר רעיון לכיוון השני?
תשובה
ההוכחה צריך להיות דו כיוונית בעיקרון. משלימים את הקבוצה האורתונורמלי לבסיס אורתונורמלי, ואז לכל וקטור יש הצגה יחידה לפי הבסיס הזה. מפרקים את המכפלות הפנימיות של הוקטור לפי חוקי הלינאריות ומקבלים את תנאי שיוויון פרסבל (זה השיוויון באי שיוויון בסל).
בנוגע לתרגיל הנוסף
בתרגיל הנוסף יש כמות נכבדת של אינטגרלים שצריך לחשב. האם מותר לבצע את תהליך האינטגרצייה במחשבון, מבלי לנמק? וזה רק אני, או שהוקטורים שמתקבלים ממש לא יפים?
- זה אשכרה התעללות, הוקטורים שיוצאים אחרי הג"ש ממש, ממש לא נוחים לחישוב..
- חישוב במחשבון הוא בסדר, המטרה היא לא לראות שאתם יודעים אינטגרלים (אפשר לעשות חישוב שניים והשאר במחשבון). דבר שני, היה צריך לזכור שכל החזקות האי זוגיות אוטומטית נמחקות, ושלישית למדנו בגרם שמידט שאפשר לשמור על מספרים יפים ורק בסוף לחלק בנורמה. לכן אין צורך להסחב עם מספרים לא יפים, הכי הרבה לרשום חלקי נורמה, ורק בתשובה הסופית להציב אותה.
שאלה
איך אפשר להוכיח ש2 הוא החסם מילרע הגדול ביותר של הקבוצה {2x^2} כאשר x>1??
תשובה
כבר אני יכול לראות מהשאלה ששכחת שהנורמה היא שורש המכפלה הפנימית של הוקטור בעצמו, כלומר 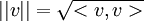 .
.
שנית, אין צורך בהוכחה מלאה באינפי, אלא הסבר יספק (למצוא את המרחק עבור x=1, ולהסביר שעם x מתקרב ל1 אזי המרחק של הוקטור מתקרב למרחק עבור x=1)
שאלה 2 תרגיל 7
הכוונה לנפח של הפוליטופ, לא לפוליטופ עצמו, כן? | (אדם אחר): מצטרף לשאלה, הרי שבתרגול עשינו את התרגיל על בדיוק אותו רעיון ושם היה נפח, ואיך אפשר לחשב פוליטופ? זה רק קבוצה אז אין פה תרגיל (אם זה לא נפח)... לכן זה חייב להיות נפח.
תשובה
קודם כל, פוליטופ אינו נפח. יש הגדרה לפוליטופ:
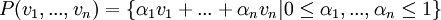
זה קבוצה של וקטורים (אמנם לא תת מרחב). נפח הוא מספר.
שנית, אתם צודקים, יש טעות בתרגיל. זה צריך להיות נפח. אני אפרסם תיקון.
שאלה:
פוליטופ הוא קבוצה של וקטורים, זאת אומרת שאם X שייך לפוליטופ הנ"ל מלמעלה אז ניתן להציגו כצירוף לינארי של הוקטורים v1....vn עם סקלרים בין 0 ל-1? זאת אומרת X=a1v1+.....anvn ?
ופוליטופ זה קבוצה, אז איך בתרגיל 1 a יש העתקה לינארית של קבוצה?
קודם כל כן, זה נובע ישירות מההגדרה של פוליטופ שציינתי למעלה.
שנית, זו לא העתקה לינראית מהקבוצה. זו העתקה לינארית מהמרחב שמכיל את הקבוצה. עכשיו אפשר להסתכל על הקבוצה של הוקטורים שמתקבלים ע"י הפעלת ההעתקה הלינארית על הפוליטופ. כלומר לקבוצה כללית 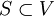 והעתקה לינארית
והעתקה לינארית 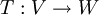 נגדיר את
נגדיר את 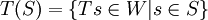
שאלה
ארז שלום, בתרגיל שעשית בכיתה, חישבת נפח פוליטופ בעזרת מטריצת מעבר, והבסיס שלפיו הצגת את הווקטורים הנתונים היה הבסיס הסטנדרטי. האם זה מותר בגלל שהבסיס הסטנדרטי הוא בא"נ? ואם כן, למה נועד תהליך גרם שמידט, למה אי אפשר פשוט תמיד לקחת את הבסיס הסטנדרטי בתור הבא"נ שלפיו אנו פועלים? תודה.
תשובה
כן, היה מותר כי הבסיס הסטנדרטי הינו בא"נ.
הבסיס הסטדנדרטי הוא בא"נ למרחבים המוכרים. אבל לתתי מרחבים אין בדר"כ בסיסים סטנדרטיים, ולשם כך צריך את תהליך גרם שמידט. למשל אם תיקח את המרחב הנפרש ע"י 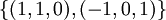 . אין לו בסיס סטנדרטי. איך תחשב מרחק של וקטורים מתת מרחב זה?
. אין לו בסיס סטנדרטי. איך תחשב מרחק של וקטורים מתת מרחב זה?
שאלה
איך אני אמור לדעת מה המספר הרציונלי הקרוב ביותר ל-שורש 2?? קשור לשאלה מס' 3 סעיף ב
תשובה
בעזרת כוח המחשבה :) זה אמנם לא קורס אינפי, אבל זו שאלה שאתם יכולים לענות עליה.
מספר שאלות די בסיסיות בנושאים שונים
1. האם המכפלה הפנימית הסטנדרטית היא מכפלה רגילה של סקלרים, או השורש של מכפלת הסקלרים (בדומה לנורמה המושרית), כלומר האם: <(1,2),(3,7)> יהיה שווה ל- 17, או לשורש של 17?
2. בתרגיל 1.a יצאה לי הוכחה די קצרה, של חצי עמוד שהשתמשה רק בהגדרת הפוליטופ (כלומר בטאתי את הקבוצה שנוצרת אם מפעילים עליה את ההעתקה, ולכן הסקלרים נשארים אותם סקלרים ורק הוקטורים עלולים להשתנות). האם זה בסדר?
3. כדי לחשב הטלה יש להשתמש בבסיס אורתונורמלי כלשהו, נכון? אבל בכיתה כשחישבת איתנו את הנפח של שלושה וקטורים לפי ההגדרה באינדוקציה רק נרמלנו את הוקטורים כדי לחשב את ההטלה. עכשיו אני מבולבל ולא יודע איך נכון לפתור את תרגיל 2.a.
תודה רבה!!
1. יהיה שווה 3+14
2. ההוכחה די קצרה בעזרת הכלה דו כיוונית.
3. אם יש לך בסיס לא אורתונורמלי עליך לנרמל אותו ואז לחשב את ההטלה.
תשובה
התשובות שענו לך נכונות פרט ל3. בכיתה לא נרמלנו את הוקטורים בלבד אלא ביצענו תהליך גרם שמידט מלא. את הוקטור הראשון נרמלנו בלבד, כי ככה עובד תהליך גרם שמידט. בכיתה נתתי נוסחא להטלה על מרחב לפי בא"נ, ולכן יש לבצע תהליך גרם שמידט על מנת שיהיה בא"נ. (לא מספיק רק לנרמל את הבסיס, צריך להפוך אותו לאורתונורמלי)
- אז בעצם בשביל לחשב את ההטלות צריך לבצע תהליך גרם שמידט על ארבעת הוקטורים בתרגיל 2?
- כן, כפי שעשינו בשיעור. שים לב שלא בכל הטלה צריך את 4 הוקטורים. כל פעם מטילים וקטור אחד על קודמיו. את המרחק צריך לחשב בין הוקטור הנתון לבין התת מרחב הנפרש ע"י קודמיו. את הבסיס של התת מרחב הזה אפשר להחליף לבא"נ בעזרת תהליך גרם שמידט
מישהו אחר- למה צריך הכלה דו כיוונית ולא פשוט שוויון ב2 a?
- מתכוון 1 a? צריך להוכיח שיוויון, כל דרך מתמטית נכונה מתקבלת. הכלה דו כיוונית זו דרך נוחה
שאלות :)
1. בשאלה 3 סעיפים א ו-ב צריך לעשות באמצעות הראש?! או להציב בנוסחא או משהו כזה , אי אפשר פשוט להגיד מתי המרחק מינימלי?
בנוסף לכך נגיד בא' כשהמרחק 2 הוא לא נמצא בקבוצת המרחקים הוא רק שואף ל2
2. בשאלה 2 a צריך להפוך את הווקטורים בקבוצה לאורתונורמליים כדי לחשב את ההיטל?
3. אני מסתבך עם 1b אפשר עזרה?
תשובה
1. צריך לרשום מה המרחק בין הוקטור הנתון לוקטור כללי בקבוצה, ואז להסביר מה יהיה החסם התחתון של המרחקים הנ"ל. המרחק לא צריך להיות בקבוצת המרחקים, הוא החסם התחתון שלה. וכפי שלמדתם באינפי, חסם תחתון לא חייב להיות בקבוצה. בנוסף אני ממליץ להסתכל על שאלה שכבר שאלו לגבי השאלה הזו, ולהזכר מה היא הגדרת הנורמה.
2. כן, לפי הנוסחא בכיתה צריך בא"נ כדי לחשב היטל ומכך מרחק.
3. תחשוב על הדרכים השונות לחשב נפח, אחת מהם תעזור לך להוכיח. צריך להזכר בסוף של לינארית 1 גם.
שאלה
המספר הרציונאלי שקרוב ביותר לשורש 2 הוא 1.4?
- מה לגבי 1.41? לא קרוב יותר? ואין מספר יותר קרוב מזה?
- אז אני לא מבין איך אפשר למצוא אותו זה יכול להיות גם 1.414 וכו' , לא?! אני לא מבין איך אפשר להגיע אליו
- המרחק המינימלי לא מתקבל. המרחק מוגדר כחסם התחתון של כל המרחקים המתקבלים. בדיוק לפי הגדרת חסם תחתון באינפי.
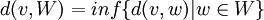
- המרחק המינימלי לא מתקבל. המרחק מוגדר כחסם התחתון של כל המרחקים המתקבלים. בדיוק לפי הגדרת חסם תחתון באינפי.
- אז אני לא מבין איך אפשר למצוא אותו זה יכול להיות גם 1.414 וכו' , לא?! אני לא מבין איך אפשר להגיע אליו
שאלה בקשר למטריצת גראם
למה |Gb| = |Gc| כאשר b,c שניהם בסיסים של V?
תשובה
זה לא נכון, מי אמר את זה?
קח בסיס אחד, תכפיל וקטור אחד שלו ב3 ותקבל בסיס שני. הדטרמיננטה של מטריצת גרם של הבסיס השני תהיה פי 9 מהדטרמיננטה של הבסיס הראשון.
- אוקי. אז זה נכון אולי עבור B וB' אחרי שעשינו לו גראם שמידט?
- לא. מטריצה גרהם של בא"נ היא תמיד
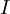 והדטרמיננטה שלה תמיד 1. הדטרמיננטה של מטריצת גרהם של בסיס כללי יכולה להיות שונה מאחד
והדטרמיננטה שלה תמיד 1. הדטרמיננטה של מטריצת גרהם של בסיס כללי יכולה להיות שונה מאחד
- בהוכחה לגבי מרחקים בהרצאה של צבאן שרצינו למצוא את הקשר למטריצת גראם, הייתה טענה ש|Gb| = |Gb'| כאשר b' הוא לאחר ביצוע תהליך גראם שמידט בלי נירמול.
- זה כבר נשמע הגיוני. הרי מותר במטריצה להוסיף לשורה מסוימת שורה אחרת כפול סקלר (כנ"ל לגבי עמודות) והדטרמיננטה תשאר אותו דבר. תהליך גרם שמידט מוסיף לכל וקטור צירוף לינארית של הוקטורים הקודמים. ולכן אם תבצע את ההתליך על מטריצת הגרהם (קודם לשורות, אחר כך לעמודות), לפי לינאריות המכפלה הפנימית, תקבל את מטריצת הגרהם של הבסיס לאחר גרם שמידט ללא נרמול. ולכן הדטרמיננטה תהיה זהה.
- בהוכחה לגבי מרחקים בהרצאה של צבאן שרצינו למצוא את הקשר למטריצת גראם, הייתה טענה ש|Gb| = |Gb'| כאשר b' הוא לאחר ביצוע תהליך גראם שמידט בלי נירמול.
- לא. מטריצה גרהם של בא"נ היא תמיד
שאלה
לא הבנתי מה הכוונה בשאלה 4. צריך למצוא את ערכם של המקדמים 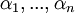 שתקיים שלכל מט' A מגודל n זה יתקיים? איך זה יכול להיות? או שצריך לתת דוגמא לA ואז למצוא את הפוליטופ כך שזה מתקיים? תוזה רבה על העזרה.
שתקיים שלכל מט' A מגודל n זה יתקיים? איך זה יכול להיות? או שצריך לתת דוגמא לA ואז למצוא את הפוליטופ כך שזה מתקיים? תוזה רבה על העזרה.
תשובה
נתונה מטריצה A ריבועית כלשהי. עכשיו צריך למצוא וקטורים 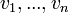 כך שיתקיים
כך שיתקיים 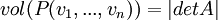 .
.
שאלה
נניח B בסיס כלשהו לW. ניקח וקטור v שלא נמצא בW. אזי {v1,..,vk,v} (נקרא לקבוצה זו B') כמובן בת"ל אך קבוצה זו אינה בסיס, נכון? אני יכולה להציג את גראם שמיט לפי B'? זה מוגדר בכלל? כי השתמשנו בזה באחת ההרצאות.
תשובה
היא בסיס, למרחב 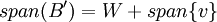 . ואת מתכוונת למטריצת גרהם של
. ואת מתכוונת למטריצת גרהם של 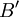 לא גראם שמידט.
לא גראם שמידט.
מטריצת גרהם מוגדרת לכל קבוצה של וקטורים, פשוט היא מעניינת יותר כאשר הוקטורים בת"ל.
חשוב לזכור שקבוצה בת"ל היא תמיד בסיס למרחב שהיא פורסת (הspan שלה).
שאלה
ארז,אנחנו רוצים אותך בתור המרצה שלנו!!!!!!
שאלה
אפשר בבקשה עזרה בתרגיל 1 ב - יש לי כיוון מסוים לגבי מטריצת המעבר אבל אני לא מצליח ליישם אותו...
תשובה
תנסה לרשום במפורש את מטריצת המעבר של הנפח של הפוליטופ מצד ימין ושל הפוליטופ מצד שמאל. בצד שמאל, השתמש בסעיף a. מה זו המטריצה שהתקבלה בצד שמאל? זכור שעל מנת לזהות מטריצת מעבר או מטריצה של העתקה צריך להראות מה המטריצה עושה לוקטורי הבסיס (בדומה להוכחות שעשינו בסוף לינארית אחד לגבי מטריצות מעבר ומטריצות מייצגות העתקה).
שאלה 2
אתה יכול להזכיר איך בדיוק מוצאים את הנפח של הפוליטופ לפי הגדרה?
תשובה
קודם כל, שימו לב שכותרת מתחילה ב== ונגמרת ב==. אל תעתיקו את התג <nowiki> מהדוגמא. הוא נמצא בתוך הטקסט על מנת שאחרי שנשמור את הדף נראה איך רושמים כותרת ולא את הכותרת עצמה.
ולעניין, מגדירים נפח פוליטופ ברקורסיה. לכל פוליטופ המורכב מוקטור אחד בלבד אנו מגדירים:
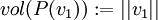 .
.
כעת, לכל פוליטופ המורכב מk וקטורים, אנו מגדירים:
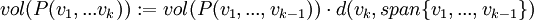
שאלה 1 ב
האם n הוא המימד של V? האם הוקטורים v1,....,vn בת"ל? יש לי הרגשה שמשהו חסר.
תשובה
לא חסר כלום. אם הוקטורים ת"ל ממילא הנפח של הפוליטופ שווה אפס ואז התשובה טריוויאלית.
- האם n הוא המימד של V?
- אוקיי, אני רואה את הבעייתיות, ואני אסביר. המרחב שמכיל את
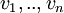 לא חייב ללהיות ממימד n כי יכול להיות שהוקטורים ת"ל. ניקח את המרחב שנפרש ע"י הוקטורים האלה, ואת
לא חייב ללהיות ממימד n כי יכול להיות שהוקטורים ת"ל. ניקח את המרחב שנפרש ע"י הוקטורים האלה, ואת 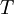 להיות העתקה מהמרחב הזה לאנשהו.
להיות העתקה מהמרחב הזה לאנשהו.
- אוקיי, אני רואה את הבעייתיות, ואני אסביר. המרחב שמכיל את
- אחרת, באמת, אפשר לקחת
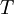 שאת הוקטורים האלה משאיר כמו שהם, אבל וקטורים אחרים במרחב מאפסת, ולכן הדטרמיננטה שלה תהיה אפס בסתירה.
שאת הוקטורים האלה משאיר כמו שהם, אבל וקטורים אחרים במרחב מאפסת, ולכן הדטרמיננטה שלה תהיה אפס בסתירה.
- אחרת, באמת, אפשר לקחת
- בקיצור,
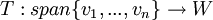
- בקיצור,
- ארז, תקן אותי אם אני טועה... אבל T חייב להיות אופרטור לינארי, כי דטרמיננטה של העתקה מוגדרת רק עבור אופרטור. לכן אני חושב שהאפשרות היחידה לפתור את התרגיל הזה היא להניח ש n=dimV.
- האמת שכנראה שאתה צודק לגבי ההגדרה של דטרמיננטה של ההעתקה ולכן זה חייב להיות אופרטור (אני צריך לרענן את זכרוני). מה שבטוח הוא, שהמימד לא חייב להיות n. יכול להיות שכל הוקטורים הנתונים הם בעצם אותו וקטור.
- אם כך, יכול להיות ש v1,...,vn אינם בסיס. כיצד נדבר על מטריצת מעבר? אפשר רמז?
- אם הם ת"ל אז הנפח הוא אפס
שאלה קטנה (בנוגע לכתיבה)
תגיד שיינר, כאשר אנחנו סתם מחשבים דברים (ולא בהוכחות או משהו כזה) האם באמת צריך לכתוב כל פעם ליניאריות ברכיב I או כמו-לינ' ברכיב II? זה די מסרבל, וזה די ברור...
- מתי היינו צריכים לכתוב את זה בתרגיל של השבוע??
תשובה
אין צורך לרשום את זה. אפשר פשוט להוציא את הסקלר (או הצמוד של הסקלר כשצריך)
שאלה 1 סעיף ב
ב1 b האם הכוונה לאופרטור לינארי כי יוצא לי נכון רק עבור אופרטורים.
בנוסף, הוכחתי שהנפח של הפוליטופ של TV1 עד TVn שווה ל |detQ| כפול הפוליטופ של V1 עד Vn בהנחה שהוקטורים בת"ל הוכחתי ש Q היא ההצגה של T מV1 עד Vn לV1 עד Vn.
V1 עד Vn הוא בסיס לתת מרחב של V. האם אני יכול שההצגה הזו היא ההצגה המייצגת של T?
תודה!
- תשובה : ב-1b אני השתמשתי בנוסחת חישוב נפח פוליטופ לפי מטריצת המעבר.
תשובה
זה נכון להעתקה לינארית ולא רק לאופרטור
נכון, דטרמיננטה מוגדרת רק על אופרטורים ולכן זה נכון.
שאלה - בנוגע לשאלה 4
ב-a - מה צריך לעשות? באופן כללי, כל מטריצה A שנקח שוקטוריה הם v1,...,vn תתאים כאן. בנוסף, אפשר לקחת וקטורים שנפח הפוליטופ שלהם הוא 1, ואת מטריצת היחידה. יש אינספור אפשרויות. מה בדיוק רצית שנעשה? -ב-b : אם הבנתי נכון, בעצם צריך ממש לכתוב את הגדרת נפח הפוליטופ כביטוי מפורש, אבל קבלתי תשובה של שורה אחת. זה בסדר?
תשובה
שימו לב לשאלה. A נתונה מה זאת אומרת כל מטריצה תתאים? לא ביקשו ממך לבחור מטריצה. בקשו ממך לבחור וקטורים בהנתן מטריצה. אי אפשר לקחת את מטריצת היחידה, כי לא נתון שA היא מטריצת היחידה. ומה הכוונה ב"וקטורי המטריצה"?
בב', אם זה הביטוי הנכון זה בסדר, צריך להסביר בשתי מילים איך הגעת אליו.
- אוקיי, אז אם A מסדר nxn, אני יכול לקחת את הוקטורים של A עצמה? כלומר, העמודה ה1 של A תהיה v1, ... העמודה ה-n של A תהיה vn, וכך לקבל שוויון נכון לכל A? (כי אם נחשב את הצגת מטריצת המעבר של הוקטורים שמצאנו (שהיא, ממש במקרה, A) לפי הבסיס הסטנדרטי נקבל שהדטרמיננטה שלה מן הסתם שווה לדטרמיננטה של A)
- כן יפה
שאלת קידבק
האם אמור להיות תרגיל 8? (מזל שזה אנונימי...)
- אני לא יודע, אבל אני מאמין שאם היה אמור להיות הוא כבר היה כאן (זה לא שהאתר נזנח, הוא התעדכן די הרבה בשבוע האחרון...)
- אל תהיה בטוח שזה כל כך אנונימי... מקורותיי בCIA אומרים לי שאת/ה גר/ה בתל-אביב, ויש 93% סיכויים שאת/ה גר/ה ברחוב הכרמל, ליד יעבץ וסמטת התבור.
- ה-CIA מאבדים את היכולות שלהם אם כך. מה ה-KGB אומרים לך?
תשובה
יהיה תרגיל, אני אפרסם אותו ביומיים הקרובים
שאלה בקשר ללכסון
נניח שנתונה לי מטריצה A מגודל n על n. מצאתי את המרחבים העצמיים שלה ומצאתי בסיס לכל מרחב עצמי. האם בטוח שאיחוד הבסיסים למרחבים העצמיים הוא קבוצה בת"ל? כלומר האם אני יכול להיות בטוח שאיחוד הבסיסים למרחבים העצמיים הוא בסיס ל F^n?
- תשובה מישהו?
שאלה
אם v,w וקטורי עמודה, A מטריצה ריבועית, אז מתקיים
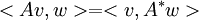 רק ביחס למכפלה הפנימית הסטנדרטית של F^n, נכון? כי רק ביחס אליה אם
רק ביחס למכפלה הפנימית הסטנדרטית של F^n, נכון? כי רק ביחס אליה אם 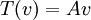 אז
אז 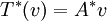 .
אשמח אם מישהו יאשר לי את זה.
.
אשמח אם מישהו יאשר לי את זה.
תשובה
זה נכון. לא הייתי אומר רק ביחס למכפלה הפנימית הסטנדרטית, אבל זה לא בהכרח נכון לכל מכפלה פנימית. יש לבדוק כל מקרה לגופו.
שאלה
ארז שלום, יש לי כמה שאלות בנוגע לתרגיל ההוא על נורמה ששומרת מכפלה פנימית יש שם כמה דברים שלא ממש הבנתי: (בהוכחה של המרוכבים) בשורה השלישית אתה הכנסת הצמדה באיבר השלישי שאני לא מבין מאיפה היא באה וגם באיבר הרביעי החלפת את המקומות של Au ו-Aw. (זה בגלל שאתה יודע ש-u ו-w ממשיים??) ואז בשורה האחרונה החלפת את ה-Re ל-מינוס Im, למה יש שם מינוס? תודה, שגיב.
תשובה
- יש שם טעות, אני עכשיו אתקן. פשוט צריך לשנות את סדר הכפל בשני האיברים. ההצמדה מגיעה משינוי הסדר (שיניתי את הסדר במקום הלא נכון).
- u וw אינם ממשיים, זו הוכחה מעל המרוכבים.
- זה נכון באופן כללי למספר מרוכב:
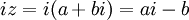 ולכן
ולכן 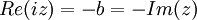 .
.
שאלה
היי ארז, יש לי שאלה לגבי פוליטופים - עוד פעם.. נניח v1,..,vn בת"ל. האם זה אומר שהם בסיס לV? באחד הדיונים למעלה כתבת שהמימד לא חייב להיות n, אז בעצם v1,..vn לא חייבים להיות בסיס...
תשובה
השאלה העיקרית היאמה זה  . בשאלה הראשונה בסופו של דבר אמרתי שזה אופרטור מהמרחב שנפרש ע"י
. בשאלה הראשונה בסופו של דבר אמרתי שזה אופרטור מהמרחב שנפרש ע"י 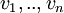 אל תוך עצמו. ולכן אם הוקטורים הללו בת"ל הם פורשים את המרחב הזה. אבל אם תיקח מרחב גדול יותר שמכיל את הוקטורים האלה, הפוליטופ שלהם יהיה אותו דבר, והנפח שלו יהיה אותו דבר. אבל במקרה זה, אופרטור מהמרחב הגדול יותר לעצמו לא יקיים את תנאי התרגיל.
אל תוך עצמו. ולכן אם הוקטורים הללו בת"ל הם פורשים את המרחב הזה. אבל אם תיקח מרחב גדול יותר שמכיל את הוקטורים האלה, הפוליטופ שלהם יהיה אותו דבר, והנפח שלו יהיה אותו דבר. אבל במקרה זה, אופרטור מהמרחב הגדול יותר לעצמו לא יקיים את תנאי התרגיל.
- כל התרגיל הזה היה בעייתי. הגענו להסכמה שT זה אופרטור. אם אתה מצמצם את התחום של האופרטור למרחב הנפרש ע"י v1,...,vn לא ניתן להוכיח את הטענה. (כי אז T כבר לא אופרטור ולכן לא מוגדרת עליו דטרמיננטה).
- זה שT אופרטור זה לא מספיק, זה עדיין לא אומר שהמימד של V הוא n. ואז בכלל אי אפשר להתייחס לv1...vn כבסיס. בהחלט תרגיל בעייתי.
שאלה בקשר לבוחן
היי ארז. אתה יכול בבקשה להעלות רשימה מדוייקת של הנושאים שיש לבוחן? ואתה יכול בבקשה להעלות גם תרגילי הכנה? תודה.
שאלה: תרגיל 8.
בתרגיל הראשון, T הוא אופרטור מV לV?
- גם אני שמתי לב לזה. יש להניח שכן כי כל העמוד מדבר על אופרטורים.