משתמש:אור שחף/133 - הרצאה/27.3.11
ישומים של אינטגרציה (המשך)
- שטח הפנים של גוף סיבוב (ללא הבסיסים): נחלק את הקטע
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) לתתי קטעים
לתתי קטעים ![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) עבור כמה k-ים. שטח הפנים הוא
עבור כמה k-ים. שטח הפנים הוא  (כאשר r רדיוס הבסיס הגדול יותר של הקונוס הנוצר בקטע=
(כאשר r רדיוס הבסיס הגדול יותר של הקונוס הנוצר בקטע=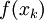 וכן
וכן 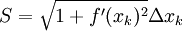 . לפי זה שטטח המעטפת כולו מקורב ע"י הסכום
. לפי זה שטטח המעטפת כולו מקורב ע"י הסכום 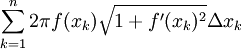 . כאשר
. כאשר 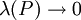 ביטוי זה שואף לאינטגרל
ביטוי זה שואף לאינטגרל 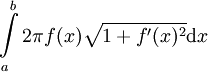 והוא שטח המעטפת לגוף הסיבוב הנוצר ע"י סיבוב
והוא שטח המעטפת לגוף הסיבוב הנוצר ע"י סיבוב 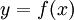 בין a ל-b סביב ציר ה-x.
בין a ל-b סביב ציר ה-x.
דוגמה
נחשב את שטח המעטפת (=שטח הפנים) של כדור בעל רדיוס r: תשובה
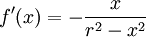 . השטח הוא
. השטח הוא 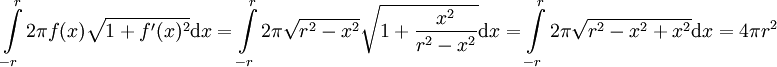
נשים לב כי שטח עיגול הוא
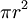 והיקפו עיבוד הנוסחה נכשל (שגיאת תחביר): \frac{\mathrm d}{\mathrm dr}\pi r^2}=2\pi r
והיקפו עיבוד הנוסחה נכשל (שגיאת תחביר): \frac{\mathrm d}{\mathrm dr}\pi r^2}=2\pi r
כמו כן שטח כדור הוא
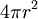 ונפחו
ונפחו 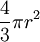 . הסבר גרף 1. מכאן שתוספת השטח
. הסבר גרף 1. מכאן שתוספת השטח 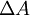 בערך שווה ל-עיבוד הנוסחה נכשל (פונקציה \pir לא מוכרת): 2\pir\Delta r
בערך שווה ל-עיבוד הנוסחה נכשל (פונקציה \pir לא מוכרת): 2\pir\Delta r
, ז"א
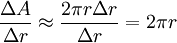 . בגבול
. בגבול 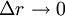 זה מדוייק:
זה מדוייק: 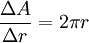 .
לעומת זאת, עבור ריבוע גרף 2 ההיקף הוא
.
לעומת זאת, עבור ריבוע גרף 2 ההיקף הוא 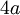 והשטח -
והשטח - 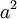 - ההיקף אינו נגזרת השטח. אבל גרף 3 היקף:
- ההיקף אינו נגזרת השטח. אבל גרף 3 היקף: 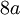 , שטח:
, שטח: 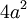 ושוב ההיקף הוא נגזרת השטח.
ושוב ההיקף הוא נגזרת השטח.
נחשב שטח פנים של כדור ללא אינטגרל: גרף 4 עפ"י שיוויון משולשים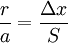 ולכן
ולכן 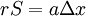 אותה חתיכת הגרף 'S' מסתובבת ליצור שטח
אותה חתיכת הגרף 'S' מסתובבת ליצור שטח  . ז"א בכל מקום שנבנה שטח ע"י סיבוב קטע באורך
. ז"א בכל מקום שנבנה שטח ע"י סיבוב קטע באורך 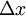 יווצר שטח באורך
יווצר שטח באורך 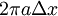 . כעת אם נסכם על כל הקטעים לאורך הקטע
. כעת אם נסכם על כל הקטעים לאורך הקטע ![[-a,a]](/images/math/1/8/8/188b8d2ccb3b1d52985a3a3e5cf71fdb.png) נבנה שטח כולל
נבנה שטח כולל 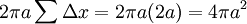 , כפי שציפינו.
, כפי שציפינו.
- בפיזיקה, כאשר כוח
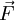 קבוע פועל בקטע באורך s אומרים שהוא עשה עבודה
קבוע פועל בקטע באורך s אומרים שהוא עשה עבודה 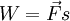 .כעת נחשב את העבודה שנעשית ע"י כוח משתנה
.כעת נחשב את העבודה שנעשית ע"י כוח משתנה 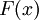 לאורך הקטע
לאורך הקטע ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) . נעשה חלוקה
. נעשה חלוקה 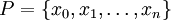 . בכל תת קטע
. בכל תת קטע ![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) ,
, 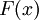 תקבל מקסימום
תקבל מקסימום 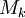 ומינימום
ומינימום 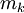 ולכן העבודה הנעשית ע"י F בקטע
ולכן העבודה הנעשית ע"י F בקטע ![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) (נקרא לה
(נקרא לה 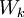 ) מקיימת
) מקיימת 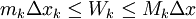 . בסה"כ העבודה לאורך הקטע היא
. בסה"כ העבודה לאורך הקטע היא 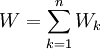 כאשר
כאשר 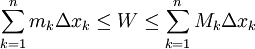 . יש כאן
. יש כאן 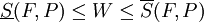 כאשר
כאשר 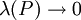 זה שואף לגבול אחד
זה שואף לגבול אחד 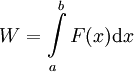 .
.
- ניוטון אומר
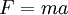 ואם מדובר בחלקיק או אדם שהולך בקו ישר (על ציר ה-x) אז התנועה שלו מתוארת ע"י הפונקציה
ואם מדובר בחלקיק או אדם שהולך בקו ישר (על ציר ה-x) אז התנועה שלו מתוארת ע"י הפונקציה 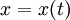 (לכל t נקודה בזמן). לפיכך מהירותו היא
(לכל t נקודה בזמן). לפיכך מהירותו היא 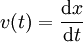 ותאוצתו
ותאוצתו 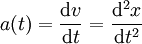 . לפי ניוטון
. לפי ניוטון 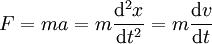 . לפי כלל השרשרת אפשר לכתוב
. לפי כלל השרשרת אפשר לכתוב 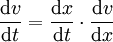 ולכן
ולכן 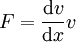 . לכן העבודה שנעשית ע"י
. לכן העבודה שנעשית ע"י 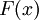 בין a ל-b היא
בין a ל-b היא ![W=\int\limits_a^b f(x)\mathrm dx=\int\limits_a^b ma(x)\mathrm dx=\int\limits_a^b m\frac{\mathrm dv}{\mathrm dt}\mathrm dx=\int\limits_a^b m\frac{\mathrm dv}{\mathrm dx}v\mathrm dx=\left[\frac{mv^2}2\right]_{x=a}^b](/images/math/3/4/e/34e71b77bf9f1d12ab9f40cdd1415522.png) . ז"א העבודה שווה לשינוי באינרגיה הקינטית.
הסבר לנוסחה:
. ז"א העבודה שווה לשינוי באינרגיה הקינטית.
הסבר לנוסחה: 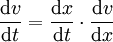 . כאן מניחים ש-
. כאן מניחים ש-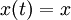 ו-
ו-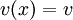 . בזה נוצרת פונקציה מרוכבת
. בזה נוצרת פונקציה מרוכבת 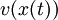 . למדנו את כלל השרשרת
. למדנו את כלל השרשרת 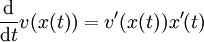 כלומר
כלומר 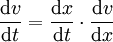 .
.
מבוא לאינטגרציה נומרית
נביא כאן 4 שיטות:
- אינטגרציה בעזרת פיתוח טיילור. לדוגמה, נחשב
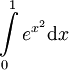 בדיוק של
בדיוק של 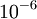 : כבר למדנו פיתוח טיילור לפונקציה
: כבר למדנו פיתוח טיילור לפונקציה 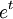 :
: 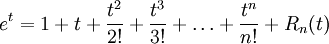 כאשר
כאשר 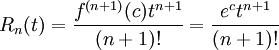 לאיזה c בין 0 ל-t. נציב
לאיזה c בין 0 ל-t. נציב 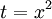 : עיבוד הנוסחה נכשל (שגיאת תחביר): e^{x^2}=1+x^2+\frac{x^4}{2!}+\frac{x^6}{3!}+\dots+\frac{x^{2n}}{n!}+R_n(x^2}
: עיבוד הנוסחה נכשל (שגיאת תחביר): e^{x^2}=1+x^2+\frac{x^4}{2!}+\frac{x^6}{3!}+\dots+\frac{x^{2n}}{n!}+R_n(x^2}
. לכן 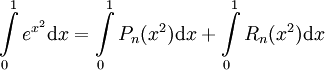 . אנו זקוקים ל-n כך ש-
. אנו זקוקים ל-n כך ש-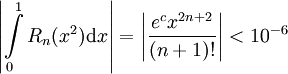 . לכל
. לכל ![x\in[0,1]](/images/math/c/6/2/c628ba2b1047de93f66cb815d986e107.png) מתקיים
מתקיים 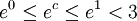 ולכן השארית חסומה ע"י
ולכן השארית חסומה ע"י 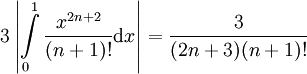 . ואכן, עבור
. ואכן, עבור 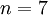 זה מספיק קטן. לפי זה
זה מספיק קטן. לפי זה 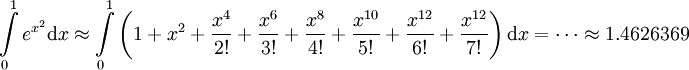 . השיטה הזאת לא תמיד מועילה כי 1) לא כל פונקציה גזירה אינסוף פעמים כדי שנוכל לחשב
. השיטה הזאת לא תמיד מועילה כי 1) לא כל פונקציה גזירה אינסוף פעמים כדי שנוכל לחשב 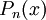 ל-n כלשהו. 2) יש פונקציות בעלות אינסוף נגזרות שפשוט לא מקורבות היטב ע"י פיתוח טיילור, ובפרט על קטע ארוך. 3) יש פונקציות שקשה לחשב את פיתוח טיילור שלהן כי הוא תלוי בנגזרת מסדר גבוה.
ל-n כלשהו. 2) יש פונקציות בעלות אינסוף נגזרות שפשוט לא מקורבות היטב ע"י פיתוח טיילור, ובפרט על קטע ארוך. 3) יש פונקציות שקשה לחשב את פיתוח טיילור שלהן כי הוא תלוי בנגזרת מסדר גבוה.
- קירוב ע"פ סכומי רימן. נניח ש-f רציפה בקטע
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . נקח
. נקח 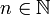 כלשהו ונעשה חלוקה שווה של
כלשהו ונעשה חלוקה שווה של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) :
: 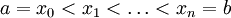 כאשר לכל k נגדיר
כאשר לכל k נגדיר 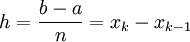 . (כאשר h הוא אורך הפסיעה בין שתי נקודות החלוקה. הקירוב לאינטגרל נתון ע"י סכום רימן
. (כאשר h הוא אורך הפסיעה בין שתי נקודות החלוקה. הקירוב לאינטגרל נתון ע"י סכום רימן 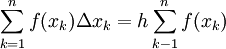 . כעת נניח ש-f בעלת נגזרת רציפה
. כעת נניח ש-f בעלת נגזרת רציפה 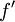 ב-
ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ונחשב את סדר גודל הטעות בקירוב הנ"ל:
ונחשב את סדר גודל הטעות בקירוב הנ"ל: 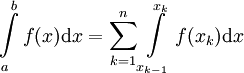 . בתוך הקטע הקטן
. בתוך הקטע הקטן ![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) נסתמך על משפט לגראנז' לומר
נסתמך על משפט לגראנז' לומר 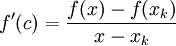 עבור c בין x ל-
עבור c בין x ל-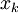 . נעביר אגף לומר
. נעביר אגף לומר 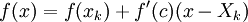 ולכן עיבוד הנוסחה נכשל (שגיאת תחביר): \int\limits_{x_{k-1}}^{x_k} f(x_k}\mathrm dx+\int\limits_{x_{k-1}}^{x_k} f'(c)(x-x_k)\mathrm dx=f(x_k)(x_k-x_{k-1})+R_k
ולכן עיבוד הנוסחה נכשל (שגיאת תחביר): \int\limits_{x_{k-1}}^{x_k} f(x_k}\mathrm dx+\int\limits_{x_{k-1}}^{x_k} f'(c)(x-x_k)\mathrm dx=f(x_k)(x_k-x_{k-1})+R_k
. 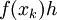 היא התרומה של קטע זה לסכום רימן. האינטגרל
היא התרומה של קטע זה לסכום רימן. האינטגרל 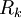 = הטעות. כעת, אם נסמן
= הטעות. כעת, אם נסמן ![m=\max_{x\in[a,b]} |f'(x)|](/images/math/2/4/7/247961448a07adc41651f241f570664d.png) ונוכל להסיק
ונוכל להסיק  .
.