משתמש:אור שחף/133 - רשימת משפטים
מתוך Math-Wiki
אינטגרלים
- אם
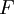 ו-
ו-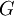 קדומות ל-
קדומות ל- בקטע
בקטע 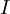 אז קיים קבוע
אז קיים קבוע 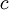 כך ש-
כך ש-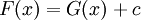 .
.
- לכל פונקציה
 מוגדרת וחסומה בקטע
מוגדרת וחסומה בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) מתקיים:
מתקיים:
- אם
 חלוקה של הקטע אזי
חלוקה של הקטע אזי 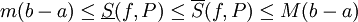 .
. - אם
 חלוקה של הקטע ו-
חלוקה של הקטע ו-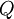 עידון של
עידון של  כך ש-
כך ש-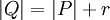 (כלומר,
(כלומר, 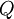 מתקבלת מ-
מתקבלת מ- ע"י הוספת
ע"י הוספת 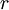 נקודות) אזי
נקודות) אזי 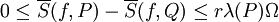 וכן
וכן 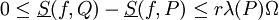 .
. - לכל שתי חלוקות
 ו-
ו-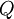 של הקטע מתקיים
של הקטע מתקיים 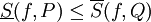 .
. - אם
 אינטגרבילית בקטע אז
אינטגרבילית בקטע אז 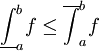 .
. - לכל חלוקה
 מתקיים
מתקיים 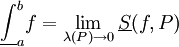 וגם
וגם 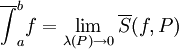 .
. -
 אינטגרבילית בקטע אם"ם
אינטגרבילית בקטע אם"ם 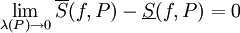 .
. -
 אינטגרבילית בקטע אם"ם לכל
אינטגרבילית בקטע אם"ם לכל  קיימת חלוקה
קיימת חלוקה  של
של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך ש-
כך ש-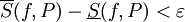 .
. - אם
 רציפה בקטע אזי היא אינטגרבילית בו.
רציפה בקטע אזי היא אינטגרבילית בו.
- הכללה: אם
 רציפה ב-
רציפה ב-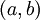 אזי היא אינטגרבילית ב-
אזי היא אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
- הכללה להכללה: אם
 רציפה ב-
רציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) פרט למספר סופי של נקודות אז
פרט למספר סופי של נקודות אז  אינטגרבילית ב-
אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
- הכללה להכללה: אם
- הכללה: אם
- נניח ש-
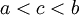 . אזי
. אזי  אינטגרבילית ב-
אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) וב-
וב-![[c,b]](/images/math/d/6/0/d6033df87877013a91e322ce6a5bc181.png) אם"ם היא אינטגרבילית ב-
אם"ם היא אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , ואם כן אז
, ואם כן אז  .
.
- הכללה: עבור
 כנ"ל ו-
כנ"ל ו-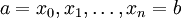 (הנקודות לאו דווקא מסודרות בסדר עולה) מתקיים
(הנקודות לאו דווקא מסודרות בסדר עולה) מתקיים 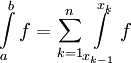 .
.
- הכללה: עבור
- תהי
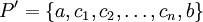 חלוקה נוספת של
חלוקה נוספת של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך ש-
כך ש-![\forall1\le k\le n:\ c_k\in[x_{k-1},x_k]](/images/math/6/9/a/69a81d3601befa0c225b704fa40e9731.png) . אזי
. אזי 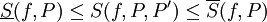 . יתר על כן,
. יתר על כן, 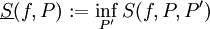 ו-
ו-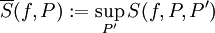 .
. - הגדרות האינטגרל לפי דרבו ולפי רימן שקולות.
- אם
- אם
 מוגדרת ומונוטונית בקטע
מוגדרת ומונוטונית בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אזי היא אינטגרבילית בו.
אזי היא אינטגרבילית בו.
- תהיינה
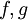 אינטגרביליות ב-
אינטגרביליות ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , ו-
, ו-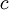 קבוע. אזי:
קבוע. אזי:
- לינאריות:
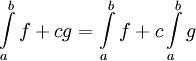 .
. - מונוטוניות: אם
![\forall x\in[a,b]:\ f(x)\ge g(x)](/images/math/b/0/f/b0f5c358a40311d0e8e99133603633c2.png) אז
אז 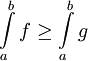 .
.
- חיוביות: בפרט מתקיים שאם
![\forall x\in[a,b]:\ f(x)\ge0](/images/math/2/8/6/286bfa2f0ea6e33a9691152f7160ba89.png) אזי
אזי 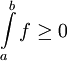 .
.
- חיוביות: בפרט מתקיים שאם
- הכללה לאי-שיוויון המשולש: אם
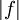 אינטגרבילית בקטע אז
אינטגרבילית בקטע אז 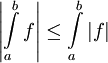 .
. - אם
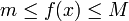 בקטע אז
בקטע אז 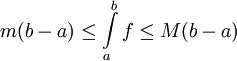 .
.
- בפרט, אם
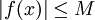 אז
אז 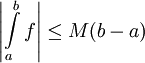 .
. - בפרט, אם
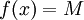 (פונקציה קבועה) אז
(פונקציה קבועה) אז 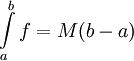 .
.
- בפרט, אם
- לינאריות:
- המשפט היסודי של חשבון אינטגרלי: תהי
 אינטגרבילית ב-
אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , ותהי
, ותהי 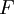 כך ש-
כך ש-![\forall x\in[a,b]:\ F(x):=\int\limits_a^x f](/images/math/0/c/5/0c5f442e2899834dd8dae25116fd3194.png) .
.
-
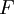 מוגדרת ורציפה ב-
מוגדרת ורציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
. - לכל
![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) שבה
שבה  רציפה,
רציפה, 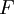 קדומה ל-
קדומה ל- (כלומר,
(כלומר, 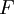 גזירה ו-
גזירה ו-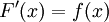 ).
). - נוסחת ניוטון-לייבניץ: נניח ש-
 רציפה ב-
רציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . אזי
. אזי ![\int\limits_a^b f=[F(x)]_{x=a}^b=F(b)-F(a)](/images/math/9/9/1/9910c3fea84d530a4ddc29cee79f0db3.png) .
.
-
- אם
 רציפה בקטע אז יש לה שם פונקציה קדומה.
רציפה בקטע אז יש לה שם פונקציה קדומה.