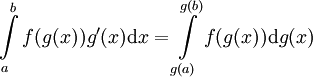משתמש:אור שחף/133 - רשימת משפטים
מתוך Math-Wiki
< משתמש:אור שחף
גרסה מ־12:58, 24 ביולי 2011 מאת אור שחף (שיחה | תרומות) (משתמש:אור שחף/133 - שונות/רשימת משפטים הועבר למשתמש:אור שחף/133 - רשימת משפטים)
במשפטים הבאים, אלא אם צויין אחרת, נסמן:
-
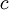 הוא קבוע.
הוא קבוע. -
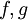 פונקציות.
פונקציות. - כל אחת מהקבוצות הבאות היא קבוצת כל הפונקציות המקיימות תכונה מסויימת בקבוצה
 :
:
-
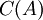 היא קבוצת כל הפונקציות הרציפות ב-
היא קבוצת כל הפונקציות הרציפות ב- .
. -
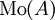 - מונוטוניות.
- מונוטוניות.
-
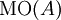 - מונוטוניות במובן הצר.
- מונוטוניות במובן הצר.
-
-
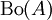 - חסומות.
- חסומות.
- החסם העליון של פונקציה ב-
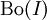 הוא
הוא 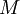 והתחתון -
והתחתון - 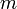 .
.
- החסם העליון של פונקציה ב-
-
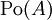 - אי-שליליות.
- אי-שליליות.
-
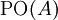 - חיוביות.
- חיוביות.
-
-
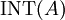 - אינטגרביליות.
- אינטגרביליות.
-
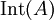 - אינטגרביליות מקומית.
- אינטגרביליות מקומית.
-
-
- אם קיימת לפונקציה פונקציה קדומה היא תסומן בעזרת האות הגדולה המתאימה (למשל, הפונקציה הקדומה של
 היא
היא 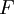 ).
). -
 היא חלוקה
היא חלוקה 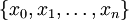 של הקטע הנתון כך ש-
של הקטע הנתון כך ש-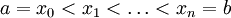 .
.
-
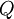 היא העדנה של
היא העדנה של  .
. -
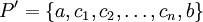 היא חלוקה נוספת של הקטע הנוצרת מהחלוקה
היא חלוקה נוספת של הקטע הנוצרת מהחלוקה  כך ש-
כך ש-![\forall1\le k\le n:\ c_k\in[x_{k-1},x_k]](/images/math/6/9/a/69a81d3601befa0c225b704fa40e9731.png) .
.
-
אינטגרלים
- אם
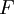 ו-
ו-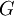 קדומות ל-
קדומות ל- בנקודה כלשהי אז קיים
בנקודה כלשהי אז קיים 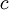 כך ש-
כך ש-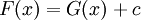 .
. -
![\forall f\in\mbox{Bo}([a,b]):\ m(b-a)\le\underline S(f,P)\le\overline S(f,P)\le M(b-a)](/images/math/7/2/2/72232dd34882080a21ed6cfeabd5874c.png) .
. - אם
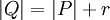 (כלומר,
(כלומר, 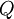 מתקבלת מ-
מתקבלת מ- ע"י הוספת
ע"י הוספת 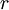 נקודות) ו-
נקודות) ו-![f\in\mbox{Bo}([a,b])](/images/math/2/8/0/280a60ed0dbeb5a05c229058c3e2dccd.png) אזי
אזי 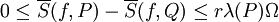 וכן
וכן 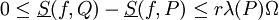 .
. - לכל חלוקה
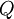 של הקטע הנתון (לאו דווקא העדנה של
של הקטע הנתון (לאו דווקא העדנה של  ), אם
), אם ![f\in\mbox{Bo}([a,b])](/images/math/2/8/0/280a60ed0dbeb5a05c229058c3e2dccd.png) אזי
אזי 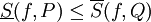 .
. - לכל
![f\in\mbox{INT}([a,b])](/images/math/d/7/5/d7508b39782132c406362c3334b761d7.png) מתקיים
מתקיים 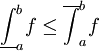 .
. - תהי
![f\in\mbox{Bo}([a,b])](/images/math/2/8/0/280a60ed0dbeb5a05c229058c3e2dccd.png) . אזי
. אזי 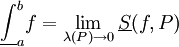 וגם
וגם 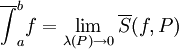 .
. - נניח ש-
![f\in\mbox{Bo}([a,b])](/images/math/2/8/0/280a60ed0dbeb5a05c229058c3e2dccd.png) .
. ![f\in\mbox{INT}([a,b])](/images/math/d/7/5/d7508b39782132c406362c3334b761d7.png) אם"ם
אם"ם 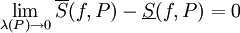 .
. - נניח ש-
![f\in\mbox{Bo}([a,b])](/images/math/2/8/0/280a60ed0dbeb5a05c229058c3e2dccd.png) .
. ![f\in\mbox{INT}([a,b])](/images/math/d/7/5/d7508b39782132c406362c3334b761d7.png) אם"ם לכל
אם"ם לכל  קיימת חלוקה
קיימת חלוקה  של
של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך ש-
כך ש-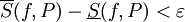 .
. - אם
![f\in C([a,b])](/images/math/b/4/7/b47de061ee9326687c356d16869abb9a.png) אז
אז ![f\in\mbox{INT}([a,b])](/images/math/d/7/5/d7508b39782132c406362c3334b761d7.png) .
.
- הכללה: אם
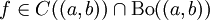 אזי
אזי ![f\in\mbox{INT}([a,b])](/images/math/d/7/5/d7508b39782132c406362c3334b761d7.png) .
.
- הכללה להכללה: אם
![f\in C([a,b]\setminus A)\cap\mbox{Bo}([a,b])](/images/math/5/f/2/5f2371fa5faaf1eff6c198dd01f6b74b.png) כאשר
כאשר  קבוצה סופית אזי
קבוצה סופית אזי ![f\in\mbox{INT}([a,b])](/images/math/d/7/5/d7508b39782132c406362c3334b761d7.png) .
.
- הכללה להכללה: אם
- הכללה: אם
- אם
![f\in\mbox{Mo}([a,b])](/images/math/6/3/d/63df8145bb9a0a0651708cfa1b7589e9.png) אז
אז ![f\in\mbox{INT}([a,b])](/images/math/d/7/5/d7508b39782132c406362c3334b761d7.png) .
. - נניח ש-
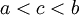 . אזי
. אזי ![f\in\mbox{INT}([a,b])\cap\Big(\mbox{INT}([a,c])\cup\mbox{INT}([c,b])\Big)](/images/math/a/7/5/a75d02f90217ac18b660ccd2701e6d65.png) אם"ם
אם"ם ![f\in\mbox{INT}([a,b])](/images/math/d/7/5/d7508b39782132c406362c3334b761d7.png) , ואם כן אז
, ואם כן אז 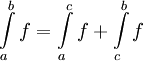 .
.
- הכללה: עבור
 כנ"ל ו-
כנ"ל ו-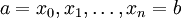 (הנקודות לאו דווקא מסודרות בסדר עולה) מתקיים
(הנקודות לאו דווקא מסודרות בסדר עולה) מתקיים 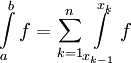 .
.
- הכללה: עבור
- אם
![f\in\mbox{Bo}([a,b])](/images/math/2/8/0/280a60ed0dbeb5a05c229058c3e2dccd.png) אז
אז 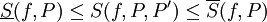 . יתר על כן,
. יתר על כן, 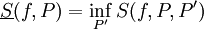 ו-
ו-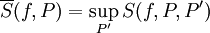 .
. - הגדרות האינטגרל לפי דרבו ולפי רימן שקולות.
- לינאריות:
![\forall f,g\in\mbox{INT}([a,b]):\ \int\limits_a^b f+cg=\int\limits_a^b f+c\int\limits_a^b g](/images/math/5/2/8/52874a1023fa42dbaeeac0118cc084a2.png) .
. - מונוטוניות: אם
![f,g\in\mbox{INT}([a,b])](/images/math/d/a/1/da19750cddd2b21d077d0e11d2312798.png) וכן
וכן ![\forall x\in[a,b]:\ f(x)\ge g(x)](/images/math/b/0/f/b0f5c358a40311d0e8e99133603633c2.png) אז
אז 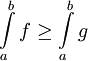 .
.
- חיוביות: בפרט מתקיים שאם
![f\in\mbox{INT}([a,b])\cap\mbox{Po}([a,b])](/images/math/2/f/e/2fed31eccdaf1ee5b9dbe729bdc9657a.png) אזי
אזי 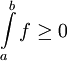 .
.
- חיוביות: בפרט מתקיים שאם
- הכללה לאי-שיוויון המשולש: אם
![|f|\in\mbox{INT}([a,b])](/images/math/1/3/9/13961f6952da26c5e8f7baa79b9424ec.png) אז
אז ![f\in\mbox{INT}([a,b])](/images/math/d/7/5/d7508b39782132c406362c3334b761d7.png) ו-
ו-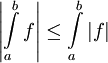 .
. - אם
![f\in\mbox{INT}([a,b])\cap\mbox{Bo}([a,b])](/images/math/7/8/d/78defd9b0a00051999f8d9ce185565f8.png) אז
אז 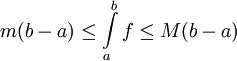 .
.
- מקרה פרטי: אם
![\forall x\in[a,b]:\ |f(x)|\le M](/images/math/1/6/b/16b3029642875feb621b346dca19885e.png) ו-
ו-![f\in\mbox{INT}([a,b])](/images/math/d/7/5/d7508b39782132c406362c3334b761d7.png) אז
אז 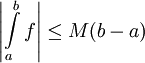 .
.
- מקרה פרטי: אם
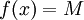 (פונקציה קבועה) אז
(פונקציה קבועה) אז 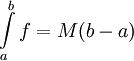 .
.
- מקרה פרטי: אם
- מקרה פרטי: אם
- המשפט היסודי של חשבון אינטגרלי: תהי
![f\in\mbox{INT}([a,b])](/images/math/d/7/5/d7508b39782132c406362c3334b761d7.png) ותהי
ותהי 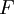 כך ש-
כך ש-![\forall x\in[a,b]:\ F(x):=\int\limits_a^x f](/images/math/0/c/5/0c5f442e2899834dd8dae25116fd3194.png) . אזי
. אזי ![F\in C([a,b])](/images/math/b/a/7/ba7ca250436aa38c291cbefd1a953629.png) וכן לכל נקודה ב-
וכן לכל נקודה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) שבה
שבה  רציפה,
רציפה, 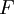 קדומה ל-
קדומה ל- (כלומר,
(כלומר, 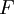 גזירה ב-
גזירה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ו-
ו-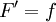 ).
). - נוסחת ניוטון-לייבניץ: תהי
![f\in C([a,b])](/images/math/b/4/7/b47de061ee9326687c356d16869abb9a.png) . אזי
. אזי ![\int\limits_a^b f=[F(x)]_{x=a}^b=F(b)-F(a)](/images/math/9/9/1/9910c3fea84d530a4ddc29cee79f0db3.png) .
. - לכל
![f\in C([a,b])](/images/math/b/4/7/b47de061ee9326687c356d16869abb9a.png) יש פונקציה קדומה.
יש פונקציה קדומה. - אינטגרציה בחלקים: נניח כי
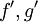 רציפות. אזי
רציפות. אזי 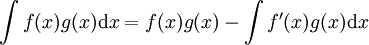 .
.
- שיטת ההצבה:
 .
.
- כל פונקציה רציונלית
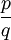 כך ש-
כך ש-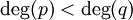 ניתנת לפירוק יחיד כסכום של שברים חלקיים
ניתנת לפירוק יחיד כסכום של שברים חלקיים 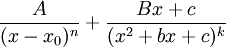 כאשר
כאשר 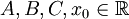 ול-
ול-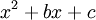 אין שורשים ממשיים.
אין שורשים ממשיים. - נפח גוף הסיבוב הנוצר מסיבוב השטח שמתחת ל-
![f\in\mbox{Po}([a,b])](/images/math/d/1/9/d19f4dce2f8f428bc1b23e133a47558a.png) בין
בין  ל-
ל-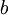 סביב ציר ה-
סביב ציר ה- הוא
הוא  .
. - הממוצע של
![f\in C([a,b])](/images/math/b/4/7/b47de061ee9326687c356d16869abb9a.png) בקטע
בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) הוא
הוא 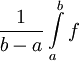 .
. - אורך הגרף של
![f\in C([a,b])](/images/math/b/4/7/b47de061ee9326687c356d16869abb9a.png) בקטע
בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) הוא
הוא 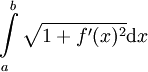 .
. - שטח המעטפת (ללא הבסיסים) של גוף סיבוב הנוצר מסיבוב הגרף של
![f\in C([a,b])](/images/math/b/4/7/b47de061ee9326687c356d16869abb9a.png) סביב ציר ה-
סביב ציר ה- בקטע
בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) הוא
הוא 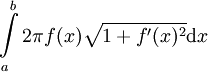 .
. - תהינה
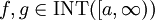 . אזי
. אזי 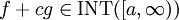 ומתקיים
ומתקיים 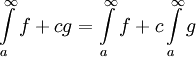 .
. - תהא
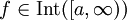 ויהי
ויהי 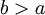 . אזי
. אזי 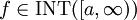 אם"ם
אם"ם 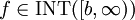 ואם כן
ואם כן 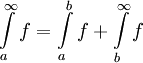 .
. -
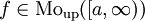 . אזי
. אזי 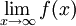 קיים אם"ם
קיים אם"ם 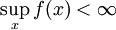 ואם כן
ואם כן 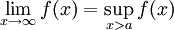 .
. -
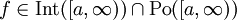 . אזי
. אזי 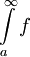 מתכנס אם"ם האינטגרלים החלקיים
מתכנס אם"ם האינטגרלים החלקיים 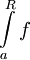 חסומים מלעיל, ואם לא אז
חסומים מלעיל, ואם לא אז 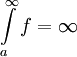 .
. - מבחן ההשוואה: נניח ש-
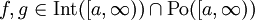 וכן
וכן 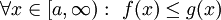 . אם
. אם 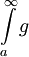 מתכנס אז
מתכנס אז 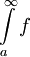 מתכנס.
מתכנס. - מבחן ההשוואה הגבולי:
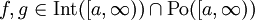 וכן
וכן 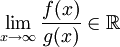 . אם
. אם 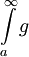 מתכנס אז
מתכנס אז 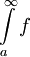 מתכנס.
מתכנס.
- מקרה פרטי: אם בפרט הגבול שונה מ-0 אז שני האינטגרלים מתכנסים ומתבדרים כאחד.
- המבחן האינטגרלי לטורים: תהא
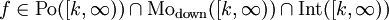 עבור
עבור 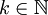 כלשהו. אזי
כלשהו. אזי  אם"ם
אם"ם 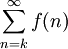 מתכנס.
מתכנס.
- הכללה: בפרט מתקיים
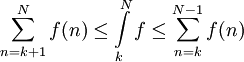 .
.
- הכללה: בפרט מתקיים
- תהא
 מוגדרת ב-
מוגדרת ב- .
. 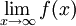 קיים אם"ם הוא מקיים את תנאי קושי בקטע.
קיים אם"ם הוא מקיים את תנאי קושי בקטע. - תהא
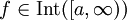 . אזי
. אזי 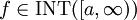 אם"ם
אם"ם 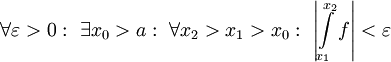 .
. - תהא
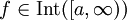 . אם
. אם  אז
אז 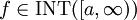 .
. - מבחן דיריכלה: תהא
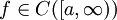 ונניח שהאינטגרלים החלקיים
ונניח שהאינטגרלים החלקיים 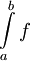 חסומים כאשר
חסומים כאשר 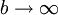 . כמו כן תהא
. כמו כן תהא 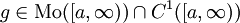 ו-
ו-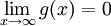 . אזי
. אזי  .
. - סכימה בחלקים:
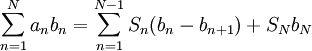 כאשר
כאשר 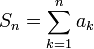 .
. - משפט דיריכלה לטורים: נניח שלטור
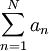 יש סכומים חלקיים חסומים ונניח ש-
יש סכומים חלקיים חסומים ונניח ש-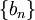 סדרה מונוטונית כך ש-
סדרה מונוטונית כך ש-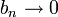 . אזי
. אזי 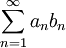 מתכנס.
מתכנס. - אם
![f,g\in\mbox{INT}((a,b])](/images/math/3/6/d/36ded8d547f124e065d0889ebdd691b4.png) אז לכל
אז לכל 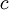 מתקיים
מתקיים 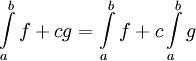 .
. - עבור
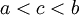 ו-
ו-![f\in\mbox{Int}((a,b])](/images/math/d/4/d/d4de390e5fe8e9419dbefee3b8325c00.png) ,
, ![f\in\mbox{INT}((a,b])](/images/math/1/8/b/18b6f609ceed15b14d60c3eb4d37a461.png) אם"ם
אם"ם ![f\in\mbox{INT}((a,c])](/images/math/8/c/4/8c479176da6ae6d24c42cde31e43273b.png) , ואם כן
, ואם כן 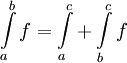 .
. - תהי
![f\in\mbox{Mo}((a,b])](/images/math/8/b/1/8b1b9791ff05b1d8eb8d6447fc1a9285.png) . אזי
. אזי 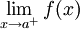 קיים אם"ם
קיים אם"ם ![f\in\mbox{Bo}((a,b])](/images/math/d/3/2/d32da08e24fcd74beef04c720db72332.png) .
. - אם
![f\in\mbox{Po}((a,b])\cap\mbox{Int}((a,b])](/images/math/3/d/b/3dbb13f1d40076f24a7117683e3ca19b.png) אז
אז ![f\in\mbox{Int}((a,b])](/images/math/d/4/d/d4de390e5fe8e9419dbefee3b8325c00.png) אם"ם האינטגרלים החלקיים
אם"ם האינטגרלים החלקיים 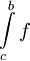 חסומים כאשר
חסומים כאשר 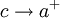 .
. - מבחן ההשוואה:
![f,g\in\mbox{Po}((a,b])\cap\mbox{Int}((a,b])](/images/math/2/a/e/2ae9e32766fdefc324812673a003a6d8.png) וכן
וכן ![\forall \in(a,b]:\ f(x)\le g(x)](/images/math/5/8/c/58c4610fb4b7f5aaf8af8d7d532b97a8.png) . אם
. אם ![g\in\mbox{INT}((a,b])](/images/math/8/0/d/80d01403ac88ff0fee775ac05e65bc96.png) אז
אז ![f\in\mbox{INT}((a,b])](/images/math/1/8/b/18b6f609ceed15b14d60c3eb4d37a461.png) .
. - מבחן ההשוואה הגבולי:
![f,g\in\mbox{Po}((a,b])\cap\mbox{Int}((a,b])](/images/math/2/a/e/2ae9e32766fdefc324812673a003a6d8.png) וקיים
וקיים 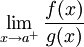 . אם
. אם ![g\in\mbox{INT}((a,b])](/images/math/8/0/d/80d01403ac88ff0fee775ac05e65bc96.png) אז
אז ![f\in\mbox{INT}((a,b])](/images/math/1/8/b/18b6f609ceed15b14d60c3eb4d37a461.png) .
.
- מקרה פרטי: אם בפרט הגבול שונה מ-0 אז שני האינטגרלים מתכנסים ומתבדרים כאחד.
- תהא
![f\in\mbox{Int}((a,b])](/images/math/d/4/d/d4de390e5fe8e9419dbefee3b8325c00.png) . אזי
. אזי ![f\in\mbox{INT}((a,b])](/images/math/1/8/b/18b6f609ceed15b14d60c3eb4d37a461.png) אם"ם
אם"ם 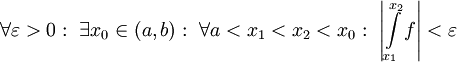 .
. - תהא
![f\in\mbox{Int}((a,b])](/images/math/d/4/d/d4de390e5fe8e9419dbefee3b8325c00.png) . אם
. אם ![|f|\in\mbox{INT}((a,b])](/images/math/e/e/3/ee31e426ac0594a9bdf2f14f1d076230.png) אז
אז ![f\in\mbox{INT}((a,b])](/images/math/1/8/b/18b6f609ceed15b14d60c3eb4d37a461.png) .
.
![\int\limits_a^b f\cdot g'=[f(x)g(x)]_{x=a}^b-\int\limits_a^b f'\cdot g](/images/math/1/9/b/19b8bd99dab83c15e4420a086d20b431.png)