88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 2
תוכן עניינים
יחסים
הגדרה: המכפלה הקרטזית של שתי קבוצות A וB הינה אוסף כל הזוגות הסדורים - 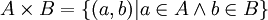 . ההבדל בין זוג סדור לבין קבוצה המכילה זוג איברים היא שהאיברים יכולים להיות שווים בזוג סדור, והסדר שלהם מהותי. כלומר שני האיברים הבאים שונים
. ההבדל בין זוג סדור לבין קבוצה המכילה זוג איברים היא שהאיברים יכולים להיות שווים בזוג סדור, והסדר שלהם מהותי. כלומר שני האיברים הבאים שונים 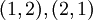 והאיבר הבא הינו זוג חוקי
והאיבר הבא הינו זוג חוקי 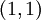 .
.
ניתן להכליל את ההגדרה לעיל לn-יה סדורה - כלומר n איברים מסודרים.
דוגמא: 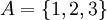 ו
ו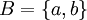 אזי מתקיים
אזי מתקיים 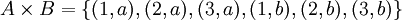
ניתן להגדיר זוגות סדורים באמצעות הגדרת הקבוצות בלבד, כפי שנראה בתרגיל הבא:
תרגיל
הוכח/הפרך:
1. ![[(a=c)\and(b=d)]\iff \{\{a\},b\}=\{\{c\},d\}](/images/math/3/6/5/3658ead84bf51f7db5fbdaced7a56889.png)
2. ![[(a=c)\and(b=d)]\iff \{\{a\},\{a,b\}\}=\{\{c\},\{c,d\}\}](/images/math/6/4/5/645b12387975b5475d0dbf00d3425a62.png)
פתרון
1. הפרכה ע"י הדוגמא הנגדית 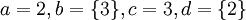
2.
הוכחה: הכיוון משמאל לימין הוא ברור. מימין לשמאל, נניח והקבוצות שוות אזי 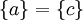 או ש
או ש 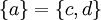 .
.
במקרה הראשון, נובע a=c ובמקרה השני נובע a=c=d, כך או כך a=c. כעת, 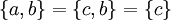 או
או 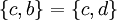 ונובע משניהם ש b=d.
ונובע משניהם ש b=d.
לכן, ניתן להגדיר זוג סדור על ידי קבוצות בלבד (באופן דומה לכך שכל המתמטיקה פחות או יותר נבנת על קבוצות בלבד).
תרגיל
הוכח שלכל קבוצות A,B,C מתקיים 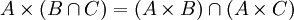
פתרון
![(x,y)\in A\times(B\cap C) \iff (x\in A) \and [(y\in B)\and (y\in C)] \iff [(x\in A)\and(y\in B)] \and [(x\in A)\and(y\in B)] \iff x\in[(A\times B)\cap(A\times C)]](/images/math/a/2/5/a258febf6c6cdcb598a7cb50cbf78115.png)
יחסים כתת קבוצה של הזוגות הסדורים
נביט בקבוצות 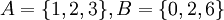 ונביט בתת הקבוצה
ונביט בתת הקבוצה 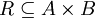 הבאה:
הבאה: 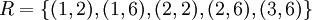 . מה מיוחד בזוגות אלה?
. מה מיוחד בזוגות אלה?
זוגות אלה הינן כל זוגות האיברים (a,b) כך ש 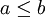 . כפי שניתן לבחור זוגות על פי יחס מסוים (במקרה זה "קטן שווה") ניתן להגדיר יחס לפי תת קבוצה מסוימת של זוגות.
. כפי שניתן לבחור זוגות על פי יחס מסוים (במקרה זה "קטן שווה") ניתן להגדיר יחס לפי תת קבוצה מסוימת של זוגות.
אם זוג מסוים נמצא בקבוצת היחס R נהוג לסמן aRb.
דוגמא: נביט בקבוצת האנשים A. נגדיר את יחס "בן של" על ידי קבוצת הזוגות הסדורים 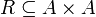 כך ש
כך ש 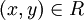 אם"ם x הוא בן של y. שימו לב שיש משמעות לכיוון היחס, שכן יש הבדל בין העובדה שאני הבן של מישהו לבין העובדה שהוא הבן שלי.
אם"ם x הוא בן של y. שימו לב שיש משמעות לכיוון היחס, שכן יש הבדל בין העובדה שאני הבן של מישהו לבין העובדה שהוא הבן שלי.
תכונות של יחסים מקבוצה לעצמה
תהי קבוצה A ויהיה יחס R המוגדר על A (כלומר, 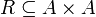 )
)
- R נקרא רפלקסיבי אם כל איבר מקיים את היחס עם עצמו ( מתקיים
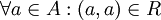 )
) - R נקרא סימטרי אם aRb גורר שגם bRa (מתקיים
![\forall a,b\in A:[(a,b)\in R \rightarrow (b,a)\in R]](/images/math/e/3/6/e369a29b5080ca819f0a865d5e33d64f.png) )
) - R נקרא טרנזיטיבי אם יחס בין ראשון לשני, ויחס בין השני לשלישי גורר יחס בין הראשון לשלישי (מתקיים
![\forall a,b,c\in A:[((a,b)\in R) \and ((b,c)\in R) \rightarrow ((a,c)\in R)]](/images/math/3/b/1/3b121b7a1bf2a808e7435d6180f38fa6.png) )
)
דוגמאות:
- יחס 'שיוויון' הינו רפלקסיבי, סימטרי וטרנזיטיבי
- יחס 'קטן שווה' הינו רפלקסיבי וטרנזיטיבי
- יחס 'קטן ממש' הינו טרנזיטיבי
- יחס 'שיוויון מודולו n' הינו רפלקסיבי, סימטרי וטרנזיטיבי
- יחס 'הכלה' הינו רפלקסיבי וטרנזיטיבי
- יחס 'a מחלק את b' הינו רפלקסיבי וטרנזיטיבי
- יחס 'אדם x שמע על אדם y' הינו רפלקסיבי
יחסי שקילות
נביט בקבוצה 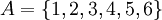 ונביט באוסף תת הקבוצות
ונביט באוסף תת הקבוצות 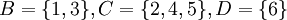 המקיימות שתי תכונות
המקיימות שתי תכונות
- הן זרות זו לו (כלומר החיתוך בין כל שתי תתי קבוצות הוא ריק)
- האיחוד של כל תתי הקבוצות שווה לקבוצה כולה

(אמנם אנחנו עוסקים בדוגמא, אבל התרגיל יהיה נכון באופן כללי לקבוצות כאלה). נגדיר את היחס R על A באופן הבא: 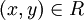 אם"ם x,y שייכים שניהם לאחד מתתי הקבוצות B,C,D.
אם"ם x,y שייכים שניהם לאחד מתתי הקבוצות B,C,D.
הוכח שR מקיים רפלקסיביות, סימטריות, וטרנזיטיביות.
פתרון
1. רפלקסיביות - נניח 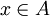 לכן x שייך לאחת מתתי הקבוצות (שכן האיחוד שלהן שווה לA) ולכן
לכן x שייך לאחת מתתי הקבוצות (שכן האיחוד שלהן שווה לA) ולכן 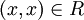 .
.
2. סימטריות - נניח 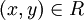 אזי
אזי 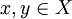 כאשר X אחת מתתי הקבוצות, מכיוון שאין משמעות לסדר שייכות לקבוצה, נובע שגם
כאשר X אחת מתתי הקבוצות, מכיוון שאין משמעות לסדר שייכות לקבוצה, נובע שגם 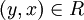 .
.
3. טרנזיטיביות - נניח ![[(x,y)\in R] \and [(y,z)\in R]](/images/math/0/b/e/0be7ba4e28716aaf8c19a241b4c93189.png) אזי אחת מתתי הקבוצות X מקיימת
אזי אחת מתתי הקבוצות X מקיימת 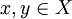 ואחת מתתי הקבוצות Y מקיימת
ואחת מתתי הקבוצות Y מקיימת  . לכן
. לכן 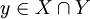 . מכיוון שהחיתוך בין תתי הקבוצות הוא ריק מוכרח להיות שX=Y ולכן
. מכיוון שהחיתוך בין תתי הקבוצות הוא ריק מוכרח להיות שX=Y ולכן 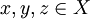 ולכן
ולכן 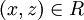 כפי שרצינו.
כפי שרצינו.
הגדרה: יחס המקיים את שלושת התכונות רפלקסיביות, סימטריות וטרנזיטיביות נקרא יחס שקילויות. כפי שראינו בתרגיל הקודם, אם אנחנו מחלקים קבוצה לתתי קבוצות זרות, היחס שמקשר בין איברי אותה קבוצה הינו יחס שקילויות. האם הכיוון ההפוך גם נכון? כלומר, האם כל יחס שקילויות מחלק קבוצה לתתי קבוצות זרות שאיחודן נותן את הקבוצה כולה.
התשובה איפוא היא כן, יחס שקילויות מחלק קבוצה לתתי קבוצות כאלה (תרגיל קל). זוהי מהותו העיקרית של יחס השקילויות - לשים לב לשקילות מסוימת בין אברים שונים (כמו שיוויון) ולצמצם את החזרות המיותרות על ידי קיבוץ כל האיברים השקולים לקבוצה אחת.
בהנתן קבוצה ויחס שקילויות על הקבוצה, נביט בכל האיברים השקולים לאיבר כלשהו (כלומר הם ביחס איתו). קבוצה זו נקראת מחלקת שקילות.
דוגמא: 0,3,6,9,... כולם ביחס השקילות "מודולו 3" באותה מחלקת שקילות. 1,4,7,10... נמצאים במחלקת שקילות אחרת.
תרגיל
תהי 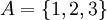 קבוצה. השלם את היחסים הבאים מעליה על מנת שיקיימו את התכונות הנדרשות בשאלה (השלם - כלומר הוסף זוגות סדורים הכרחיים):
קבוצה. השלם את היחסים הבאים מעליה על מנת שיקיימו את התכונות הנדרשות בשאלה (השלם - כלומר הוסף זוגות סדורים הכרחיים):
- השלם את
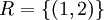 להיות יחס סימטרי וטרנזיטיבי. האם אחרי ההשלמה קיבלת יחס שקילויות?
להיות יחס סימטרי וטרנזיטיבי. האם אחרי ההשלמה קיבלת יחס שקילויות? - השלם את הקבוצה הריקה ליחס שקילויות. איך קוראים ליחס שקיבלת? מהן מחלקות השקילות?
פתרון
1. 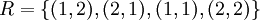 זה אינו יחס שקילויות מכיוון שאינו רפלקסיבי - (3,3) חסר.
זה אינו יחס שקילויות מכיוון שאינו רפלקסיבי - (3,3) חסר.
2. 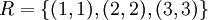 . זהו יחס השיוויון, מחלקות השקילות שלו הינן [1],[2],[3].
. זהו יחס השיוויון, מחלקות השקילות שלו הינן [1],[2],[3].
דוגמא חשובה - הגדרת הרציונאליים
נביט בקבוצת המכפלה הקרטזית של השלמים עם עצמם 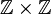 . נסתכל על ההתאמה
. נסתכל על ההתאמה 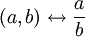 האם תחת ההתאמה הזו ניתן להגדיר את הרציונאליים באמצעות המכפלה הקרטזית לעיל בלבד?
האם תחת ההתאמה הזו ניתן להגדיר את הרציונאליים באמצעות המכפלה הקרטזית לעיל בלבד?
תשובה: לא. למשל, 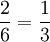 ואילו
ואילו 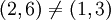 . כלומר, המכפלה הקרטזית מכילה חזרות מיותרות לעומת הרציונאליים.
. כלומר, המכפלה הקרטזית מכילה חזרות מיותרות לעומת הרציונאליים.
נרצה איפוא, להגדיר יחס שקילויות על הזוגות הסדורים של מספרים שלמים כך שכל שני שברים שקולים יהיו ביחס. שימו לב שאנו מגדירים יחס על קבוצת זוגות סדורים, ולכן האיברים ביחס הינם זוגות סדורים של זוגות סדורים. נגדיר  אם מתקיים עבור השברים
אם מתקיים עבור השברים 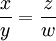 . בקיצור נרשום ש
. בקיצור נרשום ש 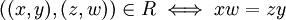 .
.
הגדרה: תהי A קבוצה ויהי R יחס שקילויות על A. אזי קבוצת המנה 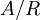 מוגדרת להיות קבוצת מחלקות השקילות של A לפי R.
מוגדרת להיות קבוצת מחלקות השקילות של A לפי R.
הערה חשובה- שימו לב שזהו סימן זהה להפרש, אך זה אינו הפרש. מידי פעם מתמטיקאים עושים את זה - מגדירים שני דברים סותרים, זה נקרא "התעללות בסמנטיקה" (abuse of notation). על אף שזה נראה שהמטרה היא להתעלל יותר בסטודנטים מאשר בסמנטיקה, לעיתים נוח יותר להשתמש בפחות סימונים, כאשר אנו מבדילים ביניהם על פי ההקשר.
מסקנה: הרציונאלים הם קבוצת המנה של הקבוצה והיחס שהגדרנו לעיל. למעשה, מאחורי כל שבר עומדת הקבוצה האינסופית של כל השברים השקולים לו, ופשוט אנחנו בוחרים לייצג קבוצה זו על ידי אחד השברים שבה באופן שרירותי (או באופן מסוים - בחירת השבר המצומצם).
שאלה ממבחן
א. תהי A קבוצה לא ריקה ותהי 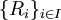 משפחה של יחסי שקילות על A. הוכיחו כי החיתוך הכללי על I הינו יחס שקילויות על A.
משפחה של יחסי שקילות על A. הוכיחו כי החיתוך הכללי על I הינו יחס שקילויות על A.
ב. נסמן 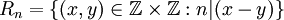 . מהם
. מהם 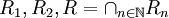 ? מהן קבוצות המנה
? מהן קבוצות המנה 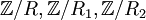 ?
?
פתרון
א. רפלקסיביות: מאחר ו 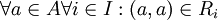 נובע ש
נובע ש 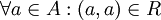 .
.
סימטריות: נניח 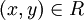 לכן
לכן 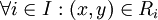 ולכן נובע מסמטריות היחסים ש
ולכן נובע מסמטריות היחסים ש 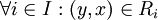 ולכן
ולכן 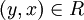 .
.
טרנזיטיביות: ממש אותו דבר...
ב. 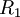 הינו אוסף כל הזוגות הסדורים מעל השלמים, שכן אחד מחלק כל מספר ולכן כל הפרש.
הינו אוסף כל הזוגות הסדורים מעל השלמים, שכן אחד מחלק כל מספר ולכן כל הפרש.
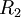 הינו אוסף כל הזוגות בהם שני הצדדים זוגיים או שני הצדדים אי זוגיים, שכן ההפרש בינהם חייב להיות זוגי.
הינו אוסף כל הזוגות בהם שני הצדדים זוגיים או שני הצדדים אי זוגיים, שכן ההפרש בינהם חייב להיות זוגי.
R הינו אוסף הזוגות שההפרש בינהם מתחלק בכל המספרים הטבעיים. רק הפרש אפס יכול להתחלק בכל מספר, ולכן R הינו אוסף הזוגות מהצורה (q,q) עבור q מספר שלם. (יחס השיוויון.)
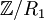 הינו אוסף מחלקות השקילות של היחס המכיל את כל הזוגות. יש בו רק מחלקת שקילות אחת המכילה את כל המספרים השלמים.
הינו אוסף מחלקות השקילות של היחס המכיל את כל הזוגות. יש בו רק מחלקת שקילות אחת המכילה את כל המספרים השלמים.
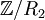 מכיל שתי קבוצות, קבוצת הזוגיים וקבוצת האי זוגיים שכן בין כל הזוגיים יש את היחס, ובין כל האי זוגיים ולא בין לבין כמובן (הרי זה יחס שקילויות כפי שקל להוכיח).
מכיל שתי קבוצות, קבוצת הזוגיים וקבוצת האי זוגיים שכן בין כל הזוגיים יש את היחס, ובין כל האי זוגיים ולא בין לבין כמובן (הרי זה יחס שקילויות כפי שקל להוכיח).
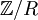 הינו אוסף כל הקבוצות המכילות איבר שלם בודד.
הינו אוסף כל הקבוצות המכילות איבר שלם בודד.