משתמש:אור שחף/133 - הרצאה/5.4.11
מתוך Math-Wiki
< משתמש:אור שחף | 133 - הרצאה
תוכן עניינים
אינטגרל לא אמיתי, סוג I (המשך)
דוגמאות חישוב
- נחשב
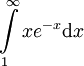 :דרך קיצור:
:דרך קיצור:![\begin{align}\int&=\lim_{R\to\infty}\int\limits_1^R xe^{-x}\mathrm dx\\&=\lim_{R\to\infty}\left[x'\cdot(-x)e^{-x}\right]_{x=1}^R-\int\limits_1^R -e^{-x}\mathrm dx\\&=\lim_{R\to\infty}-Re^{-R}+e^{-1}-[e^x]_{x=1}^R\\&=\frac2e\end{align}](/images/math/5/7/d/57df86017c24f4eee28b73fb477b584e.png)
![\int=[-xe^{-x}]_{x=1}^\infty+\int\limits_1^\infty -e^{-x}\mathrm dx=e^{-1}-[e^{-x}]_{x=1}^\infty=\frac2e](/images/math/9/4/a/94ac5db28773fb04877c1f991c45aabf.png)

-
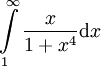 : נציב
: נציב 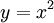 ואז כאשר
ואז כאשר 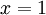 נקבל
נקבל 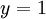 וכאשר
וכאשר 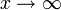 נקבל
נקבל 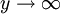 ולכן
ולכן ![\int=\int\limits_1^\infty\frac{0.5\mathrm dy}{1+y^2}=\left[\frac12\arctan(y)\right]_{y=1}^\infty=...](/images/math/f/2/8/f28e8d38ce22cac241c2ff7a7f93b915.png) .
. 
- עבור
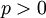 נחשב
נחשב 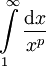 : אם
: אם 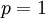 זה
זה ![\int\limits_1^\infty\frac{\mathrm dx}x=[\ln|x|]_{x=1}^\infty=\infty](/images/math/8/d/d/8ddf8650a95bc1fa2455f4b884991c83.png) , כלומר מתבדר. עבור
, כלומר מתבדר. עבור 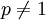 נקבל
נקבל ![\left[\frac{x^{-p+1}}{-p+1}\right]_1^\infty=\lim_{x\to\infty}\frac{x^{-p+1}}{-p+1}-\frac1{-p+1}=\begin{cases}\frac1{p-1}&p>1\\\infty&p<1\end{cases}](/images/math/3/8/1/381285b60cb92eb0ff6a4364438a4c7c.png) , כלומר האינטגרל מתכנס
, כלומר האינטגרל מתכנס  .
.  הערה: עבור
הערה: עבור 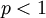 מתקבל
מתקבל 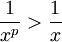 בקטע
בקטע 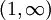 . לכן מבין הפונקציות
. לכן מבין הפונקציות 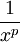 , הפונקציה המינימלית שעבורה האינטגרל על
, הפונקציה המינימלית שעבורה האינטגרל על 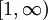 מתבדר היא
מתבדר היא  . אבל יש פונקציה מסדר גודל יותר קטן מ-
. אבל יש פונקציה מסדר גודל יותר קטן מ- שעבורן האינטגרל מתבדר, למשל
שעבורן האינטגרל מתבדר, למשל ![\int\limits_2^\infty\frac{\mathrm dx}{x\ln(x)}=\int\limits_2^\infty\frac{1/x}{\ln(x)}\mathrm dx=[\ln(\ln(x))]_{x=2}^\infty=\infty](/images/math/5/f/4/5f4ae299c93244410e52fe92e7c9e3d8.png) . "קל לבדוק" שעבור
. "קל לבדוק" שעבור 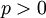 האינטגרל
האינטגרל 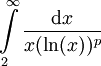 מתכנס אם"ם
מתכנס אם"ם 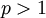 .
. - נניח ש-f מוגדרת ורציפה ב-
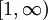 ונניח ש-
ונניח ש-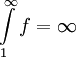 . נוכיח כי קיימת פונקציה g אי-שלילית ורציפה ב-
. נוכיח כי קיימת פונקציה g אי-שלילית ורציפה ב-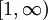 מסדר גודל יותר קטן מ-f, ז"א
מסדר גודל יותר קטן מ-f, ז"א 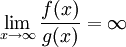 , ועדיין
, ועדיין 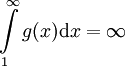 . ובכן נגדיר
. ובכן נגדיר 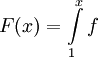 אז כמובן ש-
אז כמובן ש-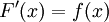 ולפי הנתון
ולפי הנתון 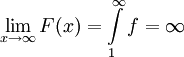 . נגדיר
. נגדיר 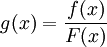 ולכן
ולכן 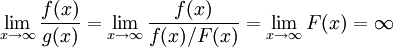 , ז"א g מסדר גודל קטן מ-f. כעת
, ז"א g מסדר גודל קטן מ-f. כעת ![\int\limits_1^\infty g=\int\limits_1^\infty\frac{f(x)}{F(x)}\mathrm dx=\int\limits_1^\infty \frac{F'(x)}{F(x)}\mathrm dx=[\ln(F(x))]_{x=1}^\infty=\infty](/images/math/e/5/2/e5211b9763bf19e88177128d3aab61e9.png) .
. 
- נניח ש-f אי-שלילית ורציפה ב-
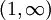 ו-
ו-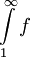 מתכנס. נוכיח שקיימת g אי-שלילת מסדר גודל גדול מ-f כך ש-
מתכנס. נוכיח שקיימת g אי-שלילת מסדר גודל גדול מ-f כך ש-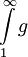 מתכנס.
מתכנס.
בנייה: נגדיר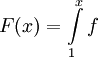 , לכן
, לכן 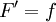 ולכן
ולכן 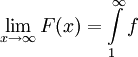 קיים ושווה ל-L. אם נגדיר
קיים ושווה ל-L. אם נגדיר 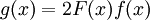 אז g מסדר גודל כמו של f וזה לא עוזר, לכן יש להגדיר
אז g מסדר גודל כמו של f וזה לא עוזר, לכן יש להגדיר 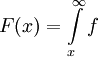 אז
אז 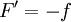 וכיוון שהאינטגרל של f מתכנס,
וכיוון שהאינטגרל של f מתכנס, 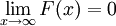 . נגדיר
. נגדיר 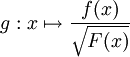 . חילקנו את f בפונקציה ששואפת ל-0 באינסוף, ולכן g מסדר גודל יותר גדול מ-f. יתר על כן
. חילקנו את f בפונקציה ששואפת ל-0 באינסוף, ולכן g מסדר גודל יותר גדול מ-f. יתר על כן![\begin{align}\int\limits_1^\infty g=&\int\limits_1^\infty\frac{f(x)}\sqrt{F(x)}\mathrm dx\\&=\int\limits_1^\infty\frac{-F'(x)}\sqrt{F(x)}\mathrm dx\\&=\left[-2\sqrt{F(x)}\right]_{x=1}^\infty\\&=2\sqrt{F(1)}\\&=2\sqrt{\int\limits_1^\infty f}\end{align}](/images/math/e/4/7/e47a4764c63d1257b8e95361182ec060.png)

-
![\int\limits_0^\infty \cos(x)\mathrm dx=[\sin(x)]_{x=0}^\infty\not\in\mathbb R\cup\{\pm\infty\}](/images/math/e/3/4/e3487bf445abc7a7cf7d97e8f59af7d5.png) , כלומר האינטגרל מתבדר לחלוטין.
, כלומר האינטגרל מתבדר לחלוטין. 
- נתבונן באינטגרל
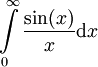 - מתכנס או מתבדר? נוכיח שמתכנס בעזרת משפט לייבניץ על טורים. נבחר N טבעי ונבטא את האינטגרל החלקי (כאשר
- מתכנס או מתבדר? נוכיח שמתכנס בעזרת משפט לייבניץ על טורים. נבחר N טבעי ונבטא את האינטגרל החלקי (כאשר 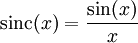 ):
): 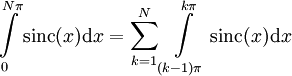 . נסמן
. נסמן 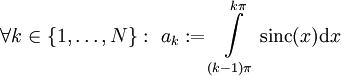 . טענה: המספרים
. טענה: המספרים 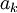 מקיימים
מקיימים 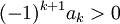
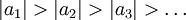 (ולכן הטור שמתפתח הוא טור לייבניץ).
(ולכן הטור שמתפתח הוא טור לייבניץ).
- אם k אי-זוגי אז
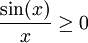 בקטע
בקטע ![[(k-1)\pi,k\pi]](/images/math/e/a/2/ea2a8ada2777316098b00da46203bf30.png) ואם k זוגי אז
ואם k זוגי אז 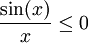 בקטע. לכן הטענה הראשונה מתקיימת.
בקטע. לכן הטענה הראשונה מתקיימת. - לכל k טבעי
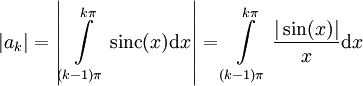 כי
כי 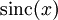 בעלת סימן קבוע ב-
בעלת סימן קבוע ב-![[(k-1)\pi,k\pi]](/images/math/e/a/2/ea2a8ada2777316098b00da46203bf30.png) . נציב
. נציב 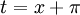 על מנת לקבל
על מנת לקבל 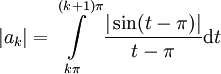 ומכיוון ש-
ומכיוון ש-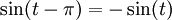 זה שווה ל-
זה שווה ל-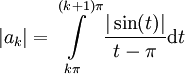 ואילו
ואילו 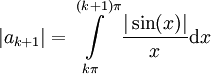 , ומכיוון ש-
, ומכיוון ש-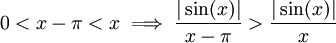 הטענה השנייה מתקיימת.
הטענה השנייה מתקיימת.
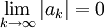 . ואכן
. ואכן 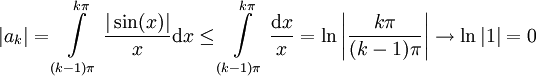 . לסיכום
. לסיכום 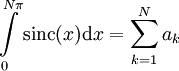 וה-
וה-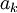 יוצרים טור לייבניץ. ע"פ משפט ליבניץ הטור
יוצרים טור לייבניץ. ע"פ משפט ליבניץ הטור 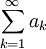 מתכנס, נאמר ל-L. טענה:
מתכנס, נאמר ל-L. טענה: 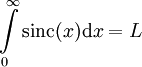 . הוכחה: יהי
. הוכחה: יהי  נתון. לפי הנתון קיים
נתון. לפי הנתון קיים 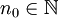 כך שלכל
כך שלכל 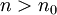 מתקיים
מתקיים 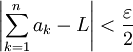 . כמו כן
. כמו כן 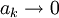 ולכן קיים
ולכן קיים 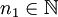 כך שלכל
כך שלכל 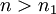 מתקיים
מתקיים 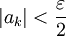 . אם
. אם 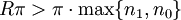 אזי
אזי 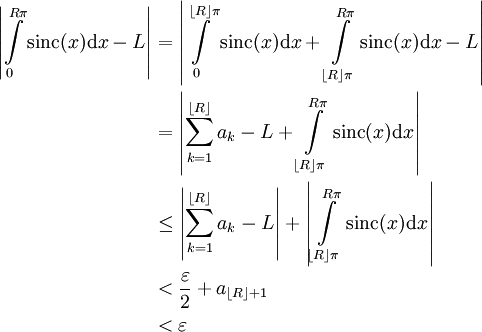

משפט 1
נניח שהפונקציות f ו-g מוגדרות ואינטגרביליות בקטע  ו-c מספר קבוע. אזי הפונקציה
ו-c מספר קבוע. אזי הפונקציה 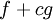 אינטגרבילית ב-
אינטגרבילית ב- ומתקיים
ומתקיים 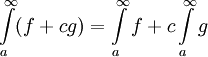 .
.
הוכחה
לפי הגדרה 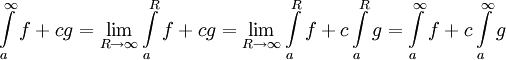 .
. 
משפט 2
תהי f מוגדרת ואינטגרבילית מקומית ב- ויהי
ויהי 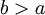 . אזי האינטגרל
. אזי האינטגרל 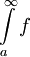 מתכנס אם"ם
מתכנס אם"ם 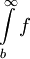 מתכנס, ואם כן
מתכנס, ואם כן 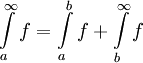 . ההוכחה פשוטה.
. ההוכחה פשוטה.
משפט 3
- תהי f מוגדרת ועולה בקטע
 . אזי
. אזי 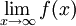 קיים אם"ם
קיים אם"ם 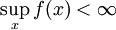 , ואם כן
, ואם כן 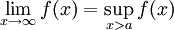 .
. - תהי f מוגדרת ואינטגרבילית מקומית ב-
 . עוד נניח ש-
. עוד נניח ש-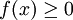 בקטע זה, אזי
בקטע זה, אזי 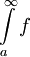 מתכנס אם"ם האינטגרלים החלקיים
מתכנס אם"ם האינטגרלים החלקיים 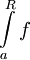 חסומים מלעיל.
חסומים מלעיל.
הוכחות
- נניח
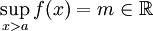 . טענה:
. טענה: 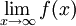 קיים ושווה ל-m. הוכחה: לפי אפיון החסם העליון, אם
קיים ושווה ל-m. הוכחה: לפי אפיון החסם העליון, אם  אזי קיים
אזי קיים 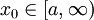 כך ש-
כך ש-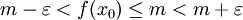 לכן עבור כל
לכן עבור כל 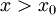 מתקיים (מכיוון ש-f עולה)
מתקיים (מכיוון ש-f עולה) 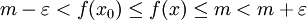 . בפרט, לכל
. בפרט, לכל 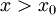 מתקיים
מתקיים 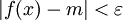 ולכן
ולכן 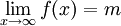 ואם
ואם  (לא חסום) אז לכל
(לא חסום) אז לכל 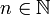 קיים
קיים  כך ש-
כך ש-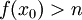 . כעת, אם
. כעת, אם 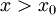 אז
אז 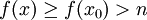 . נובע ש-
. נובע ש-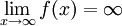 ואין גבול במובן הצר.
ואין גבול במובן הצר. 
- לכל
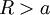 נגדיר
נגדיר 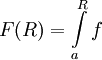 . כיוון ש-
. כיוון ש-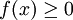 לכל
לכל 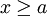 ,
, 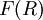 עולה עם R. האינטגרל הלא אמיתי מקיים
עולה עם R. האינטגרל הלא אמיתי מקיים 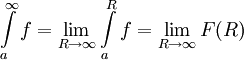 וראינו בסעיף 1 שהגבול של
וראינו בסעיף 1 שהגבול של 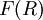 קיים אם"ם
קיים אם"ם 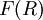 חסומה מלעיל, ז"א אם"ם
חסומה מלעיל, ז"א אם"ם 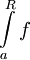 חסום מלעיל כאשר
חסום מלעיל כאשר 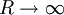 .
. 
מסקנה
מתוך ההוכחה ראינו שאם האינטגרל הלא אמיתי של פונקציה אינטגרבילית מקומית אי-שלילית מתבדר אז הוא מתכנס במובן הרחב ל-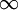 .
.