שיחה:88-133 אינפי 2 תשעב סמסטר ב/כלליות

חזרה לדף הקורס

גלול לתחתית העמוד

הוספת שאלה חדשה

הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).

-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן

אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.

שאלות

למה לא לומדים כלום?

הקצב הוא בערך רבע ממה שהיה בסמסטר א'. זה ישאר ככה?

כרגע אין תרגול. ואולי זה נראה לאט כי חקירת פונקציות נראית ברורה. בכל אופן נושאי הקורס מופיעים (פחות או יותר) במערך התרגול --ארז שיינר

מי המתרגילים של הקורס הזה?

תודה

כך נכתב באתר האוניברסיטה (פריא"ל ומידע אישי):

בקבוצה של פרופ' אגרנובסקי: ארז שיינר ואורפז תורג'מן.

בקבוצה של ד"ר שיין: ארז שיינר.

בקבוצה של ד"ר הורוביץ: מתן פתאל.

מקווה שעזרתי. גל.

שאלה 2.ב. עמ' 291 במיזלר

צ"ל: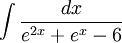$\int \frac{dx}{e^{2x}+e^{x}-6}$. אפשר עזרה? פירקתי לשברים חלקיים ואין לי מושג מה הלאה

הייתי מכפיל את המונה והמכנה ב-e^x, ואז מציב t=e^x. אחרי זה הייתי משתמש בשיטת פירוק לשברים חלקיים וממשיך כרגיל, ואז זה הרבה יותר קל. מקווה שעזרתי. גל.

תודה על העזרה... יצא תרגיל ארוך :P

יש בסוף בוחן שבוע הבא?

לא הבנתי

נבדוק את העניין --ארז שיינר

שאלה 2 תרגיל 1

נניח $f(x)$ פונקציה מוגדרת על הקטע $[a,c]$, וקיימת לה פונקציה קדומה בקטעים $[a,b];(b,c]$. הפונקציה הקדומה של $f(x)$ זה לא: $F(x)=\begin{cases} \int f(x_{1})dx_{1} & \text{ if } x_{1}\in [a,b] \\ \int f(x_{2})dx_{2} & \text{ if } x_{2}\in (b,c] \end{cases}$  ?

באם אענה לך תשובה מלאה לעניין אסגיר את הפתרון לשאלה (לפחות כפי שעולה כרגע בעיני רוחי). ממליץ לבדוק את תכונות הפונקציה בנקודה x=b, והאם הן תתקיימנה לכל פונקציות ולכל קטע שנקח. האם תמיד תתקיים רציפות? האם תמיד תתקיים גזירות? אכוון אותך ואומר לך: מהו תנאי הכרחי לגזירות? מה יקרה אם הוא לא ייתקיים בנקודה מסויימת בקטע? באיזו נקודה זה לא ישפיע על הנתונים? (אם בכלל קיימת כזו). התשובה לשאלה שלך תלויה בתשובה לשאלות אלו. גל.

לאיזו קבוצה/ות האתר מיועד(בנושא אינפי 2)?

תיכוניסטים, מתמטיקאים, מדמ"ח וכו'...

כולן--ארז שיינר

שאלה 3

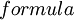$formula$אם אני מבין נכון הפונקצייה שבתוך סימן האינטגרל מקבלת את הערך של X ל-X גדול מ-X בריבוע שזה מתקיים ל-X בין 0 ל-1 ושל X בריבוע כאשר X בריבוע גדול מ-X שזה מתקיים ל-X גדול מ-1 או קטן מ-0. כדי לקבל פונקצייה שניגזרתה היא הפונקצייה הנ"ל צריך להגדיר שהיא תהיה שווה ל- X בריבוע חלקי 2 לכל X בקטע [0,1] ול-X בשלישית חלקי 3 לכל X שמחוץ לקטע זה. לפונקצייה זו יש ניגזרת ימנית בנקודה X=1 השווה ל-X בריבוע וניגזרת שמאלית השווה ל-X לכן היא איננה גזירה בנקודה זו. לכן פונקצייה זו אינה יכולה להיות פונקצייה קדומה לפונקצייה הנ"ל. האם נכון לומר שלפונקציה הנ"ל אין פונקצייה קדומה?

דבר ראשון, אין זו שאלה בנושא אינטגרלים? מדוע היא בשאלות כלליות?

שנית, אין כזה דבר "הנגזרת בנקודה אחת היא איקס בריבוע". נגזרת בנקודה היא מספר ממשי, או לא קיימת. ניתן לפי הגדרת הנגזרת (בעזרת גבולות) להוכיח שהפונקציה אינה גזירה אם זה מה שאתה חושב, או להוכיח שהיא כן גזירה (אם זה מה שאתה חושב) --ארז שיינר

חובת הגשת תרגילים

יש חובת הגשה?

לא--ארז שיינר

לאף אחד אין? גם לא למדעי המחשב?

למתי צריך להגיש את התרגיל הראשון?

תודה

שבוע הקרוב או הזה שאחריו --ארז שיינר

אינפי 1- מערכי תרגול סדרות

היי, כאן שואלים על מערכי התרגול של אינפי 1, נכון? במידה וכן, במערך התרגול הבא: http://math-wiki.com/index.php?title=88-132_אינפי_1_סמסטר_א%27_תשעב/מערך_תרגול/סדרות/גבול בתרגיל לגבי שלילת הגבול העוסק בסדרה (1-) בחזקת n: האם ניתן להימנע מההנחה כי L אי שלילי ע"י שימוש באי שוויון המשולש?

לא...פה זה אינפי 2 D:

אבל אני אענה לך בכל זאת. הוכחת התרגיל נעשתה בשיטת ההוכחה בשלילה, כלומר - מניחים משהו ואז מראים שבכל מקרה תצא סתירה - כלומר שההנחה שגויה,וזה אומר שהיא לא נכונה.

אפשר,אך הדרך שבה פתרו מקלה עלינו לפתור. --Arielipi 10:27, 29 במרץ 2012 (IST)

אממ..אני לא חושבת שהבנת למה התכוונתי- אין לי בעיה עם העובדה שהניחו בשלילה. יש לי בעיה עם ההנחה הנוספת. ש L אי שלילי. אתה לא חושב שלהפעיל אי שוויון המשולש יותר פשוט מלהניח הנחה נוספת? לדעתי אם מתאפשר אז עדיף (וארז אמר לשאול פה שאלות נראה לי).