משתמש:אור שחף/133 - הרצאה/22.2.11
את משפט 2 לא סיימנו בשיעור הקודם ולכן השלמנו זאת ב־22.2.11. חלק זה מופיע בסיכום השיעור הקודם ולא בדף הנוכחי.
תוכן עניינים
האינטגרל לפי דרבו (המשך)
משפט 3
תהי f מוגדרת וחסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . אזי
. אזי 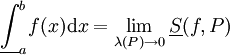 וכן
וכן 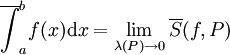 .
.
הוכחה
הטענה הראשונה אומרת שלכל 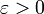 קיים
קיים 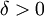 כך שאם
כך שאם 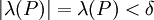 אזי
אזי 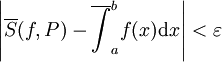 . ברור מהגדרת האינטגרל העליון כי
. ברור מהגדרת האינטגרל העליון כי 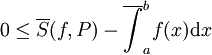 . כעת יהי
. כעת יהי 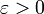 נתון. לפי הגדרת האינפימום קיימת חלוקה מסויימת Q של
נתון. לפי הגדרת האינפימום קיימת חלוקה מסויימת Q של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך ש-
כך ש-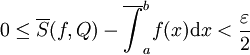 ונניח של-Q יש r נקודות חלוקה. כעת נניח ש-P חלוקה כלשהי של
ונניח של-Q יש r נקודות חלוקה. כעת נניח ש-P חלוקה כלשהי של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך ש-
כך ש-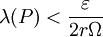 , ונגדיר
, ונגדיר 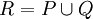 . כיוון ש-R עידון של Q,
. כיוון ש-R עידון של Q, 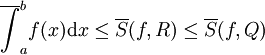 ונובע ש-
ונובע ש-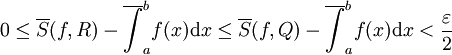 . אבל R התקבלה מ-P ע"י הוספה של לכל היותר r נקודות, לכן ע"פ משפט 2 ידוע ש-
. אבל R התקבלה מ-P ע"י הוספה של לכל היותר r נקודות, לכן ע"פ משפט 2 ידוע ש-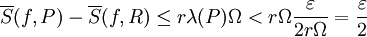 . לכן נוכל להסיק
. לכן נוכל להסיק
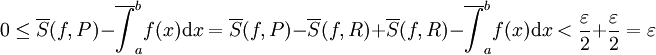 .
.
ההוכחה לאינטגרל התחתון דומה. 
משפט 4
תהי f כנ"ל. אזי f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אם"ם
אם"ם 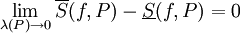 ואם כן
ואם כן 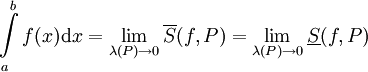 .
.
הוכחה
תחילה נניח ש-f אינטגרבילית, ז"א 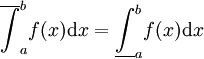 . לכן, ממשפט 3,
. לכן, ממשפט 3, 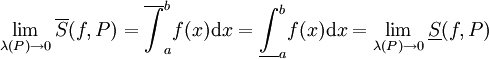 . ע"פ אריתמטיקה של גבולות
. ע"פ אריתמטיקה של גבולות 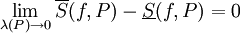 וכן
וכן 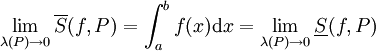 .
.
עכשיו נניח ש-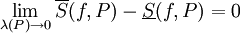 ונוכיח את ההיפך. ממשפט 3
ונוכיח את ההיפך. ממשפט 3 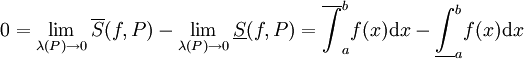 ולכן f אינטגרבילית.
ולכן f אינטגרבילית. 
משפט 5
תהי f כנ"ל. אזי f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אם"ם לכל
אם"ם לכל 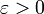 קיימת חלוקה P של
קיימת חלוקה P של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך ש-
כך ש-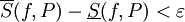 .
.
הוכחה
אם נתון ש-f אינטגרבילית אז ממשפט 4 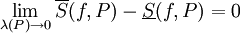 . לכן עבור
. לכן עבור 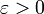 קיים
קיים 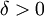 כך שלכל P המקיימת
כך שלכל P המקיימת 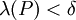 מתקיים
מתקיים 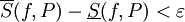 .
.
לצד השני, נניח שלכל 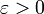 קיימת חלוקה P כך שמתקיים
קיימת חלוקה P כך שמתקיים 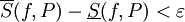 . כידוע, לכל חלוקה P מתקיים
. כידוע, לכל חלוקה P מתקיים 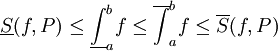 . לפי הנתון נקבל
. לפי הנתון נקבל 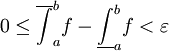 . זה נכון לכל
. זה נכון לכל 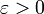 ולכן
ולכן 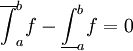 , כלומר f אינטגרבילית ב-
, כלומר f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
. 
משפט 6
תהי f רציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . אזי f אינטגרבילית ב-
. אזי f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
הוכחה
יהי 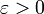 . כיוון ש-f רציפה בקטע סגור
. כיוון ש-f רציפה בקטע סגור ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) היא רציפה במ"ש, לכן קיים
היא רציפה במ"ש, לכן קיים 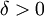 כך שאם
כך שאם ![x_1,x_2\in[a,b]](/images/math/7/9/6/796b580b3cc8423dee93c2c4cda68438.png) ו-
ו-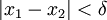 אז
אז 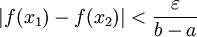 . כעת תהי P חלוקה כלשהי של
. כעת תהי P חלוקה כלשהי של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך ש-
כך ש-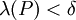 . לפיכך
. לפיכך 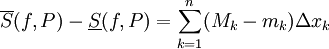 כאשר
כאשר 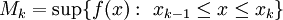 ו-
ו-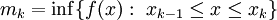 . כיוון ש-f רציפה ושעפ"י המשפט השני של ויירשראס לכל f רציפה ב-
. כיוון ש-f רציפה ושעפ"י המשפט השני של ויירשראס לכל f רציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) יש שם נקודות מינימום ומקסימום, לכל k קיימים
יש שם נקודות מינימום ומקסימום, לכל k קיימים ![y_k,z_k\in[x_{k-1},x_k]](/images/math/5/b/1/5b139ea3a75ba891882b90f1eae3ee92.png) כך ש-
כך ש-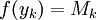 ו-
ו-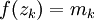 . כעת
. כעת 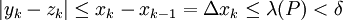 , לכן
, לכן 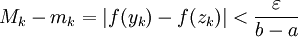 ולבסוף
ולבסוף
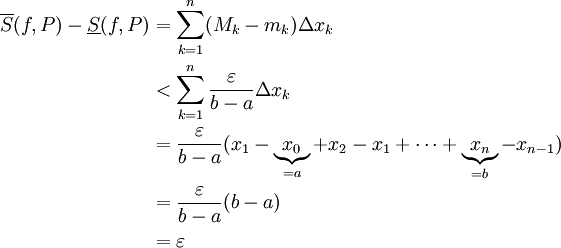
ונובע ממשפט 5 (או 4) ש-f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
. 
משפט 7
תהי f מוגדרת ומונוטונית בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . אזי f אינטגרבילית ב-
. אזי f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
הוכחה
נוכיח לפונקציה עולה. לכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) מתקיים
מתקיים 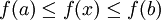 ולכן f חסומה. כעת ניקח חלוקה
ולכן f חסומה. כעת ניקח חלוקה 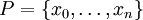 כלשהי של
כלשהי של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) המקיימת לכל k,
המקיימת לכל k, 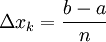 (ובפרט הם שווים) אזי
(ובפרט הם שווים) אזי 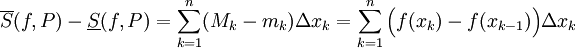 .
.
מכאן נובע כי
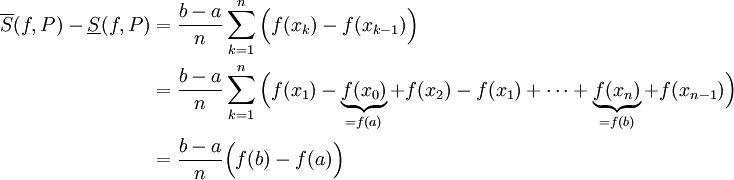
נשאיף 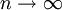 ואגף ימין שואף ל-0. מכאן ש-
ואגף ימין שואף ל-0. מכאן ש-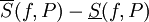 קטן כרצוננו, וקיימנו את התנאי של משפט 5. לכן f אינטגרבילית ב-
קטן כרצוננו, וקיימנו את התנאי של משפט 5. לכן f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
. 