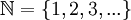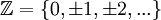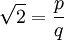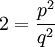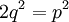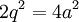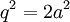מכינה למחלקת מתמטיקה/מערכי שיעור/1
על מספרים ומה שביניהם
הפעם הראשונה שאנו לומדים לספור היא בעזרת האצבעות- אצבע אחת, שתי אצבעות וכן הלאה. במתמטיקה אנו קוראים למספרים האלה טבעיים ומסמנים:
לעומת פעולת החיבור הטבעית, פעולת החיסור הידועה לא בדיוק קיימת. מה שאנו מכנים חיסור, הוא למעשה חיבור במספר נגדי. המספרים הטבעיים ביחד עם אפס והמספרים הנגדיים נקראים שלמים ומסומנים:
באופן דומה, אנו רוצים לכפול במספר הופכי (חצי, שליש, וכדומה) על מנת לבצע פעולת חילוק. אנו מגדירים את המספרים הראציונאליים בתור כל השברים של שני מספרים שלמים ומסמנים:
 (שימו לב לסימון
(שימו לב לסימון 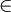 האומר שייך לקבוצה. כמובן שבכיתה ובהמשך נבהיר את הרישום המתמטי)
האומר שייך לקבוצה. כמובן שבכיתה ובהמשך נבהיר את הרישום המתמטי)
שאלה: האם כעת תיארנו את כל המספרים שאנו מכירים?
תשובה: לא. נוכיח כעת כי המספר 'שורש 2', כלומר הפתרון למשוואה 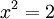 אינו מספר רציונאלי. לו שורש 2 היה מספר רציונאלי, היה ניתן להציג אותו כשבר מצומצם:
אינו מספר רציונאלי. לו שורש 2 היה מספר רציונאלי, היה ניתן להציג אותו כשבר מצומצם:
נעלה את שני האגפים בריבוע, ונקבל:
ולכן
כלומר p הינו מספר זוגי. נסמן אם כך 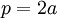 . ולכן:
. ולכן:
נחלק ב2 את שני האגפים ונקבל
כלומר גם q הינו מספר זוגי. אבל זה לא ייתכן, כיוון שהצגנו את שורש 2 כשבר מצומצם. לכן הגענו לסתירה המצביעה על העובדה שההנחה שלנו היא לא נכונה. ההנחה שלנו כמובן היא ששורש 2 הוא מספר רציונאלי.