מדר קיץ תשעב/סיכומים/תקציר
מתוך Math-Wiki
תוכן עניינים
משפטים חשובים
- משפט הקיום והיחידות למד״ר מסדר 1 בצורה נורמלית: תהי
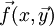 פוקנציה וקטורית המקיימת את תנאי ליפשיץ ב־
פוקנציה וקטורית המקיימת את תנאי ליפשיץ ב־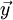 בתיבה
בתיבה ![B=[x_0-a,x_0+a]\times\prod_{k=1}^n[y_{0,k}-b_k,y_{0,k}+b_k]](/images/math/b/e/2/be2e9ad58b7a71cfdeba11cb14dc042c.png) , ונתונים תנאי ההתחלה
, ונתונים תנאי ההתחלה 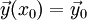 . אזי למערכת יש פתרון אחד בדיוק בקטע
. אזי למערכת יש פתרון אחד בדיוק בקטע 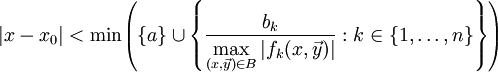 .
. - כל מד״ר מסדר
 שקולה למערכת של
שקולה למערכת של  מד״ר מסדר 1:
מד״ר מסדר 1: 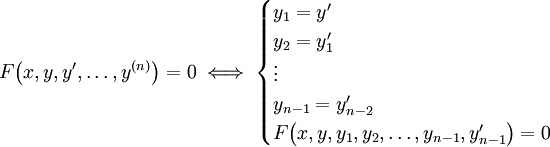 . כמו כן, המערכת נורמלית/לינארית/לינארית־הומוגנית בהתאם למד״ר המקורית.
. כמו כן, המערכת נורמלית/לינארית/לינארית־הומוגנית בהתאם למד״ר המקורית.
שיטות לפתרון מד״ר
מד״ר מסדר 1
- מד״ר בצורה דיפרנציאלית עם משתנים מופרדים היא מהצורה
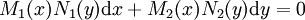 . אם
. אם 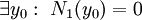 אזי
אזי 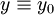 פתרון, ואם
פתרון, ואם 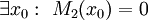 אזי
אזי 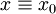 פתרון. אחרת
פתרון. אחרת 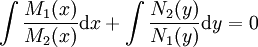 .
. - נתונה מד״ר
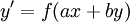 . אז נציב
. אז נציב 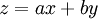 ו־
ו־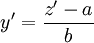 .
.
- הכללה: נתונה מד״ר
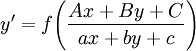 . אם
. אם 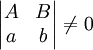 נציב
נציב 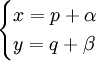 כאשר
כאשר 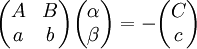 ונקבל
ונקבל 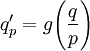 . אחרת נבחר
. אחרת נבחר 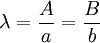 ונציב
ונציב 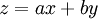 .
.
- הכללה: נתונה מד״ר
- מד״ר הומוגנית: נתונה מד״ר
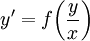 . אזי נציב
. אזי נציב 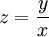 ו־
ו־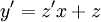 .
. - מד״ר לינארית: נתונה מד״ר
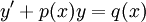 . אם היא לינארית־הומוגנית אזי
. אם היא לינארית־הומוגנית אזי 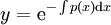 , ובכל מקרה
, ובכל מקרה 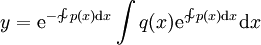 .
. - משוואת ברנולי: נתונה מד״ר
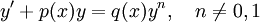 . נציב
. נציב 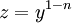 , כאשר אם
, כאשר אם 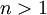 אז
אז 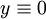 פתרון רגולרי (כאשר הקבוע החופשי שואף ל־
פתרון רגולרי (כאשר הקבוע החופשי שואף ל־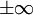 ), אם
), אם 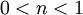 אז פתרון סינגולרי, ואם
אז פתרון סינגולרי, ואם 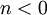 אז לא פתרון. הפתרונות הרגולריים:
אז לא פתרון. הפתרונות הרגולריים: ![y=\sqrt[1-n]{\mathrm e^{-(1-n)\sim\!\!\!\!\int p(x)\mathrm dx}\int(1-n)q(x)\mathrm e^{(1-n)\sim\!\!\!\!\int p(x)\mathrm dx}\mathrm dx}](/images/math/d/2/1/d21060ddd088f406161a14104fc4c1e8.png) .
. - מד״ר מהצורה
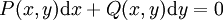 היא מדויקת אם״ם יש
היא מדויקת אם״ם יש 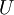 כך ש־
כך ש־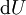 שווה לאגף ימין, מה שמתרחש אם״ם
שווה לאגף ימין, מה שמתרחש אם״ם 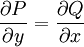 .
.
- אם המד״ר אינה מדויקת ניתן לנסות להכפיל אותה ב־
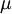 כך שתהפוך למדויקת.
כך שתהפוך למדויקת. 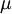 תלויה רק ב־
תלויה רק ב־ אם״ם
אם״ם 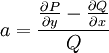 תלויה רק ב־
תלויה רק ב־ , ואז
, ואז 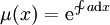 . היא תלויה רק ב־
. היא תלויה רק ב־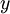 אם״ם
אם״ם 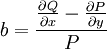 תלויה רק ב־
תלויה רק ב־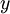 , ואז
, ואז 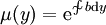 .
.
- אם המד״ר אינה מדויקת ניתן לנסות להכפיל אותה ב־
- משוואת ריקרטי: מד״ר מהצורה
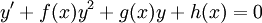 . הפתרון הכללי הוא מהצורה
. הפתרון הכללי הוא מהצורה 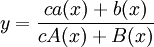 . אם
. אם 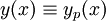 פתרון אזי
פתרון אזי 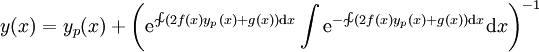 הפתרון הכללי.
הפתרון הכללי. - נתונה מד״ר
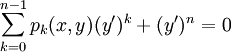 ממעלה
ממעלה  . אזי קיימות פונקציות
. אזי קיימות פונקציות 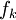 שעבורן
שעבורן 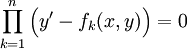 .
. - אם
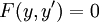 נציב
נציב 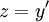 ואז
ואז  . בנוסף, אם
. בנוסף, אם 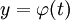 ו־
ו־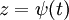 אזי
אזי 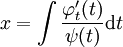 .
. - אם
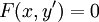 נציב
נציב 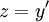 ואז
ואז 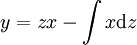 . בנוסף, אם
. בנוסף, אם 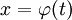 ו־
ו־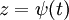 אזי
אזי 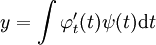 .
. - שיטת פיקארד: נתונה בעיית ההתחלה
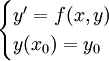 . נבחר פונקציה
. נבחר פונקציה 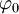 שעבורה
שעבורה 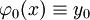 , וניצור ממנה את סדרת הפונקציות המקיימת
, וניצור ממנה את סדרת הפונקציות המקיימת 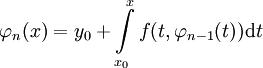 . במידה והסדרה הנ״ל מוגדרת היטב (כלומר, כל האינטגרלים קיימים)
. במידה והסדרה הנ״ל מוגדרת היטב (כלומר, כל האינטגרלים קיימים) 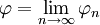 היא פתרון של הבעיה.
היא פתרון של הבעיה. - משוואת קלרו: נתונה המד״ר
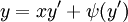 . אזי
. אזי 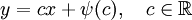 או (כאשר
או (כאשר 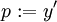 )
) 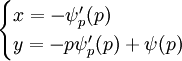 .
. - משוואת לגראנז׳: נתונה המד״ר
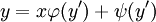 עבור
עבור 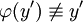 . נציב
. נציב 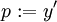 ואז
ואז 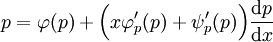 . לפיכך
. לפיכך  מקיים
מקיים 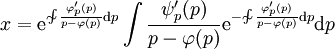 או
או 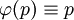 (מקרה זה יש לבדוק בנפרד), ו־
(מקרה זה יש לבדוק בנפרד), ו־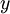 מקיים
מקיים  .
.
מד״ר מסדר 2
- בהנתן מד״ר
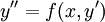 או
או 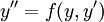 נציב
נציב 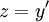 ונקבל
ונקבל 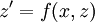 או
או 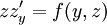 , בהתאמה. מתקיים
, בהתאמה. מתקיים 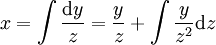 ו־
ו־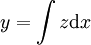 .
.
מד״ר מכל סדר
מד״ר לינארית
בפרק זה, אלא אם צוין אחרת, המד״ר היא 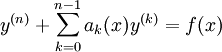 .
.
- אם המד״ר לינארית־הומוגנית אז מרחב הפתרונות שלה הוא מרחב וקטורי.
- אם בנוסף המד״ר מקיימת את משפט הקיום והיחידות אזי מרחב הפתרונות
 מימדי.
מימדי.
- אם בנוסף המד״ר מקיימת את משפט הקיום והיחידות אזי מרחב הפתרונות
- ורונסקיאן: עבור קבוצת פונקציות
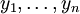 מגדירים
מגדירים 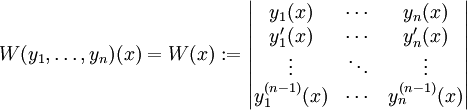 .
.
- אם
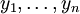 ת״ל אזי
ת״ל אזי 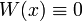 .
. - אם
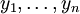 פתרונות של מד״ר לינארית־הומוגנית המקיימת את תנאי משפט הקיום והיחידות בתחום
פתרונות של מד״ר לינארית־הומוגנית המקיימת את תנאי משפט הקיום והיחידות בתחום 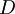 וכן
וכן 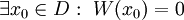 אזי הם ת״ל.
אזי הם ת״ל.
- אם
- משפט ליוביל: אם
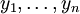 פתרונות בת״ל של המד״ר והיא הומוגנית אזי
פתרונות בת״ל של המד״ר והיא הומוגנית אזי 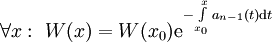 .
. - הפתרון הכללי של המד״ר הוא
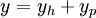 , כאשר
, כאשר 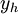 הפתרון הכללי של המד״ר הלינארית־הומוגנית המתאימה ו־
הפתרון הכללי של המד״ר הלינארית־הומוגנית המתאימה ו־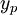 פתרון פרטי כלשהו של המד״ר.
פתרון פרטי כלשהו של המד״ר. - וריאציית הפרמטרים: נתונים
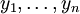 פתרונות בת״ל של המד״ר הלינארית־הומוגנית המתאימה. אזי הפתרון הכללי של המד״ר הוא
פתרונות בת״ל של המד״ר הלינארית־הומוגנית המתאימה. אזי הפתרון הכללי של המד״ר הוא 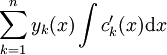 כאשר
כאשר 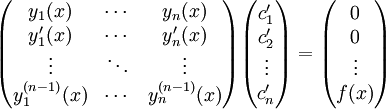 . באופן שקול:
. באופן שקול: 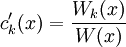 , כאשר
, כאשר 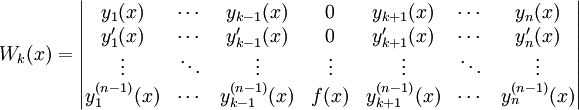 .
. - נניח שהמד״ר לינארית־הומוגנית עם מקדמים קבועים. אזי נציב
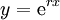 , ולכן
, ולכן 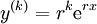 וגם
וגם 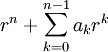 (זה הפולינום האופייני של המשוואה) שווה ל־0. אם השורשים השונים זה מזה הם
(זה הפולינום האופייני של המשוואה) שווה ל־0. אם השורשים השונים זה מזה הם 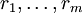 והריבויים שלהם
והריבויים שלהם 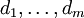 בהתאמה אזי הפתרון הכללי הוא
בהתאמה אזי הפתרון הכללי הוא 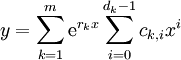 . אם
. אם 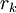 אינו ממשי ניתן לכתוב
אינו ממשי ניתן לכתוב 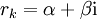 ואז, כיוון ש־
ואז, כיוון ש־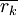 שורש עם אותו ריבוי, נציב
שורש עם אותו ריבוי, נציב 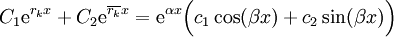 .
.
- שיטת הניחוש/הבחירה/המקדמים הנעלמים: נניח שהמד״ר לינארית עם מקדמים קבועים וכן
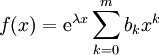 , כאשר
, כאשר  קבועה (יכולה להיות גם 0), והריבוי של
קבועה (יכולה להיות גם 0), והריבוי של  בפולינום האופייני הוא
בפולינום האופייני הוא 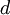 (במידה ו־
(במידה ו־ לא שורש נאמר
לא שורש נאמר 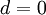 ). אזי קיים פתרון פרטי מהצורה
). אזי קיים פתרון פרטי מהצורה 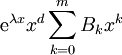 כאשר
כאשר 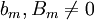 . הערה: אם
. הערה: אם 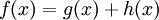 נוכל לפתור עבור
נוכל לפתור עבור 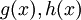 בנפרד ולסכום את הפתרונות הפרטיים.
בנפרד ולסכום את הפתרונות הפרטיים.
- שיטת הניחוש/הבחירה/המקדמים הנעלמים: נניח שהמד״ר לינארית עם מקדמים קבועים וכן
- משוואת אוילר(־לגראנג׳) היא מד״ר לינארית מהצורה
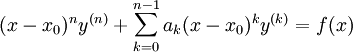 עם
עם 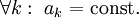 . מציבים
. מציבים 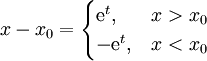 במד״ר ההומוגנית ואז
במד״ר ההומוגנית ואז 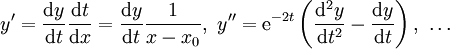 . נקבל משוואה לינארית־הומוגנית עם מקדמים קבועים, וניתן להמשיך לפתור אותה באופן זה. לחלופין, אנו לומדים מכך שאפשר להציב
. נקבל משוואה לינארית־הומוגנית עם מקדמים קבועים, וניתן להמשיך לפתור אותה באופן זה. לחלופין, אנו לומדים מכך שאפשר להציב 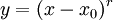 במד״ר ההומוגנית ולקבל
במד״ר ההומוגנית ולקבל 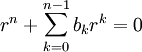 (משוואה אינדיציאלית). אם השורשים השונים זה מזה הם
(משוואה אינדיציאלית). אם השורשים השונים זה מזה הם 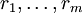 והריבויים שלהם
והריבויים שלהם 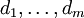 בהתאמה אזי הפתרון ההומוגני הכללי הוא
בהתאמה אזי הפתרון ההומוגני הכללי הוא 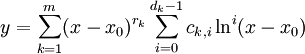 . אם
. אם 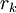 אינו ממשי ניתן לכתוב
אינו ממשי ניתן לכתוב 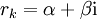 ואז, כיוון ש־
ואז, כיוון ש־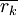 שורש עם אותו ריבוי, נציב
שורש עם אותו ריבוי, נציב 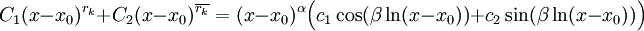 .
.
- אם
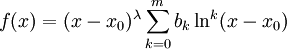 כאשר
כאשר  קבועה (יכולה להיות גם 0), והריבוי של
קבועה (יכולה להיות גם 0), והריבוי של  במשוואה האינדיציאלית הוא
במשוואה האינדיציאלית הוא 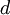 (אם לא שורש
(אם לא שורש 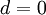 ). אזי קיים פתרון פרטי מהצורה
). אזי קיים פתרון פרטי מהצורה 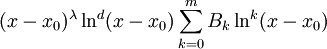 כאשר
כאשר 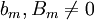 .
.
- אם
פתרון מד״ר באמצעות טורי חזקות
- נתונה מד״ר מהצורה
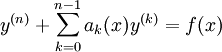 כאשר
כאשר 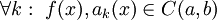 ותהי
ותהי 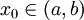 . אם
. אם  וכל המקדמים
וכל המקדמים 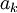 אנליטיים סביב
אנליטיים סביב  עם רדיוס התכנסות
עם רדיוס התכנסות 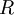 או יותר אזי קיים פתרון אנליטי סביב
או יותר אזי קיים פתרון אנליטי סביב  של המד״ר עם רדיוס התכנסות
של המד״ר עם רדיוס התכנסות 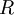 או יותר.
או יותר. - טור פרוביניוס הוא טור מהצורה
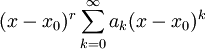 .
. - בהנתן
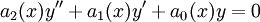 נחלק ב־
נחלק ב־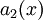 . תהי
. תהי  נקודה סינגולרית של
נקודה סינגולרית של 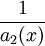 . אם קיימים הגבולות
. אם קיימים הגבולות 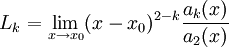 הנקודה נקראת סינגולרית־רגולרית. בקרבת
הנקודה נקראת סינגולרית־רגולרית. בקרבת  נקבל
נקבל 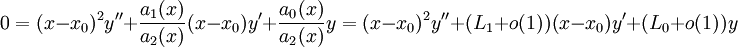 . לפי משפט, אם
. לפי משפט, אם  נקודה סינגולרית־רגולרית אזי קיים פתרון אנליטי למד״ר סביב
נקודה סינגולרית־רגולרית אזי קיים פתרון אנליטי למד״ר סביב  בצורת בצורת טור פרוביניוס. לכן נפתור עבור
בצורת בצורת טור פרוביניוס. לכן נפתור עבור 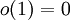 , נציב
, נציב 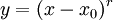 ונקבל את הפתרונות בצורת טורים של המד״ר עם
ונקבל את הפתרונות בצורת טורים של המד״ר עם 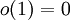 (אם פתרונות הפולינום האופייני של המד״ר עם
(אם פתרונות הפולינום האופייני של המד״ר עם 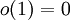 הם
הם 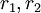 אז
אז  פתרון פרטי). נציב פתרונות אלו במד״ר המקורית ונקבל את מקדמי הטורים.
פתרון פרטי). נציב פתרונות אלו במד״ר המקורית ונקבל את מקדמי הטורים.
הערה: נאמר ש־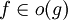 אם
אם 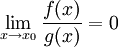 . לעתים כותבים "
. לעתים כותבים "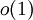 " לציון איבר הנמצא בקבוצה זו, ולא הקבוצה עצמה.
" לציון איבר הנמצא בקבוצה זו, ולא הקבוצה עצמה.
- משוואת בסל:
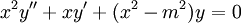 . מתקיים
. מתקיים 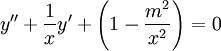 ולכן
ולכן 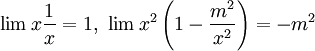 , כלומר
, כלומר 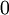 סיגולריות־רגולרית.
סיגולריות־רגולרית. - פונציית גמא:
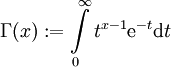 . היא מקיימת
. היא מקיימת 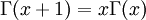 וגם
וגם 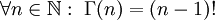 .
. - משוואת אוילר:
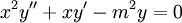 .
.
- משוואת בסל: