88-341 תשעג סמסטר א/תרגילים/תרגיל 4

שאלה 1

הוכיחו את ההכללה הבאה של התוצאה שהבאנו בתרגול. נדרש רק שינוי קל של ההוכחה שניתנה:

יהיו 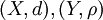$(X,d),(Y,\rho)$ מרחבים מטריים, $U \subseteq X$ קבוצה פתוחה, ו- $f:U \to Y$ פונקציה כלשהי. הראו כי קבוצת הנקודות בהן $f$ רציפה היא מטיפוס $G_\delta$

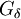
שאלה 2

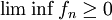א. תזכורת: למת פאטו אומרת שאם לכל $n$ הפונקציה $f_n:X \to [0,\infty]$ מדידה, אזי $\liminf f_n \ge 0$ מדידה, ומתקיים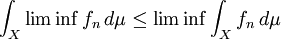 $\int_X \liminf f_n \, d\mu \leq \liminf \int_X f_n \, d\mu$

תנו דוגמא לסדרת פונקציות בממ"ח $([0,1],L(\mathbb{R}) \cap [0,1],m)$ שבה האי שוויון בלמת פאטו הוא $0 \leq 1$.

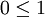רמז: בנו סדרה של פונקציות חסומות ורציפות למקוטעין 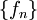$\{ f_n \}$ המקיימות 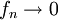$f_n \to 0$ אבל $\int_{[0,1]} f_n \, d\mu=1$ לכל $n$.

ב. האם משפט ההתכנסות המונוטונית של לבג נכון גם לגבי סדרת יורדת של פונקציות מדידות ואי שליליות? (כלומר 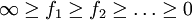$\infty \ge f_1 \ge f_2 \ge \dots \ge 0$). אם כן הוכיחו ואם לא תנו דוגמא נגדית.

שאלה 3

א. חשבו את הגבול הבא: (אתם רשאים להניח שהשיטות לחישוב אינטגרלים מאינפי', כמו המשפט היסודי, עובדות גם עבור אינטגרלי לבג)

$\lim_{n \to \infty} \int_0^n \frac{n \sin \frac{x}{n}}{x(1+x^2)} \, dm(x)$

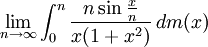
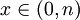רמז: כדי להראות עליה ב-$n$, התייחסו ל-$n$ כמשתנה רציף והראו כי הנגזרת של הביטוי לפיו אי-שלילית, כל עוד $x \in (0,n)$. הסתמכו על כך שאם $t \in [0,1]$ אזי $\tan(t) \ge t$.

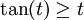ב. הוכיחו כי לכל 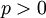$p>0$ מתקיים $\sum_{k=1}^\infty \frac{1}{(p+k)^2}=\int_0^1 \frac{x^p}{x-1} \log x \, dm(x)$.

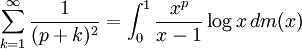רמז: משפט ההתכנסות המונוטונית של לבג.

בהצלחה!