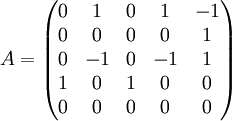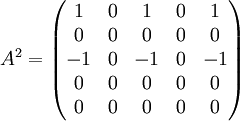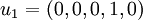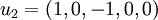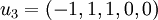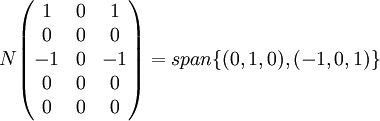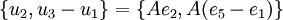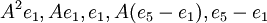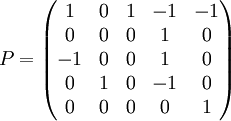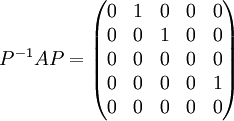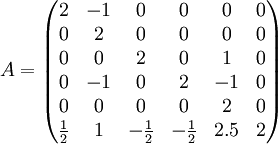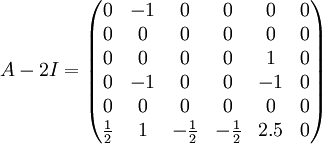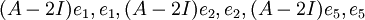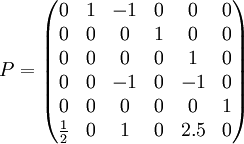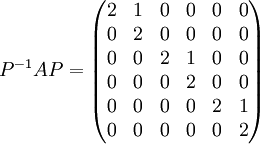משפט ז'ורדן
תוכן עניינים
בלוק ז'ורדן
בלוק ז'ורדן הינו מטריצה ריבועית מהצורה
לדוגמא,
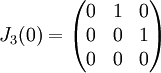 ,
, 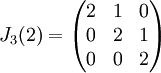
נזכר בסימון של סכום ישר של מטריצות, לדוגמא:
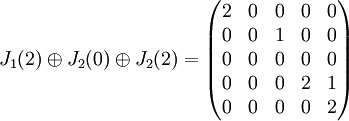
משפט ז'ורדן
תהי A מטריצה ריבועית, כך שהפולינום האופייני שלה מתפרק לגורמים לינאריים. אזי A דומה למטריצה אלכסונית בלוקים, כאשר כל בלוקיה הם בצורת ג'ורדן. בנוסף, צורה זו יחידה עד כדי סדר הבלוקים.
הוכחה ומציאת מטריצה מז'רדנת
סיכום בנושא משפט ז'ורדן על ידי דר' בועז צבאן
אלגוריתם לז'ירדון מטריצה
תהי A מטריצה כך שהפולינום האופייני שלה מתפרק לגורמים לינאריים.
- נמצא את הפולינום המינימלי של המטריצה A. נסמן את הערכים העצמיים של המטריצה ב
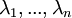
- עבור כל ע"ע
 נמצא בסיס מז'רדן עבור המרחב העצמי המוכלל
נמצא בסיס מז'רדן עבור המרחב העצמי המוכלל 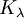 באופן הבא:
באופן הבא:
- נסמן ב k את החזקה של הגורם האי פריק
 בפולינום המינימלי
בפולינום המינימלי
- נסמן ב k את החזקה של הגורם האי פריק
- נמצא בסיס ל
![V_\lambda\cap C([A-\lambda I]^{k-1})](/images/math/b/6/d/b6dd6823f05735ca69ac6932bb03a07c.png) באופן הבא:
באופן הבא:
- נמצא בסיס ל
- נביט במטריצה
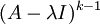 ונבחר עמודות
ונבחר עמודות ![C_{i_1}([A-\lambda I]^{k-1}),...,C_{i_p}([A-\lambda I]^{k-1})](/images/math/f/d/4/fd40dbad563c10eaac8b827e3bfd27af.png) המהוות בסיס למרחב העמודות
המהוות בסיס למרחב העמודות ![C([A-\lambda I]^{k-1})](/images/math/f/d/c/fdc466d36107abfefd49f5fb0512a475.png)
- נביט במטריצה
- נפתור את מערכת המשוואות
![x_1(A-\lambda I)C_{i_1}([A-\lambda I]^{k-1}) + ... + x_p(A-\lambda I)C_{i_p}([A-\lambda I]^{k-1})=0](/images/math/1/6/1/16104f844876e3595ac7ba6568d56656.png)
- נפתור את מערכת המשוואות
- לכל וקטור
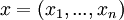 בבסיס למרחב הפתרונות למערכת נסמן
בבסיס למרחב הפתרונות למערכת נסמן 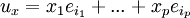 . הערה: שימו לב כי תמיד מתקיים
. הערה: שימו לב כי תמיד מתקיים 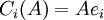 כאשר
כאשר 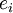 הוקטור ה-i בבסיס הסטנדרטי.
הוקטור ה-i בבסיס הסטנדרטי.
- לכל וקטור
- עבור כל וקטור x בבסיס למרחב הפתרונות נוסיף את כל הוקטורים במסלול
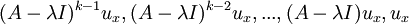 לבסיס בסדר משמאל לימין.
לבסיס בסדר משמאל לימין.
- עבור כל וקטור x בבסיס למרחב הפתרונות נוסיף את כל הוקטורים במסלול
- באופן דומה נמצא בסיס עבור
![V_\lambda\cap C([A-\lambda I]^{k-2})](/images/math/a/5/b/a5b3e456c52c7737ef62cf496f57d171.png) ונוסיף ממנו איברים לבסיס שמצאנו עד כה ובלבד שלא תיווצר תלות לינארית.
ונוסיף ממנו איברים לבסיס שמצאנו עד כה ובלבד שלא תיווצר תלות לינארית.
- באופן דומה נמצא בסיס עבור
- נמשיך בתהליך עבור
![V_\lambda\cap C([A-\lambda I]^{k-3}),...,V_\lambda](/images/math/a/6/5/a652fba00e00fed605dfa1991a38fdba.png) עד שיהיו לנו וקטורים בבסיס כמספר הריבוי האלגברי של
עד שיהיו לנו וקטורים בבסיס כמספר הריבוי האלגברי של  .
.
- נמשיך בתהליך עבור
- נאחד את הבסיסים המז'רדנים למרחבים המוכללים לכדי בסיס B למרחב כולו, זהו הבסיס המז'רדן של המטריצה
- נשים את איברי הבסיס B בעמודות מטריצה P. מתקיים כי
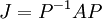 הינה צורת הז'ורדן של המטריצה A.
הינה צורת הז'ורדן של המטריצה A.
דוגמאות
ז'ירדון של מטריצה ניליפוטנטית
מצאו בסיס מז'רדן למטריצה הבאה:
- ראשית, נחשב את הפולינום האופייני
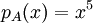 , כלומר זוהי מטריצה ניליפוטנטית
, כלומר זוהי מטריצה ניליפוטנטית
- שנית, נמצא את הפולינום המינימלי
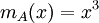 , בפרט המטריצה ניליפוטנטית מסדר 3
, בפרט המטריצה ניליפוטנטית מסדר 3
- כעת נמצא בסיס ל
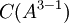 מהצורה
מהצורה 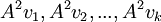 באופן הבא:
באופן הבא:
- נבחר עמודות של המטריצה
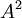 המהוות בסיס ל-
המהוות בסיס ל- 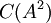
- כל עמודה i שבחרנו ניתן להציג כ-
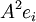
- נבחר עמודות של המטריצה
לכן בסיס למרחב העמודות הינו 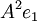
- כעת המסלול
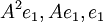 הוא חלק של הבסיס המז'רדן משמאל לימין. שימו לב שסדר הוקטורים בבסיס המז'רדן חשוב מאד.
הוא חלק של הבסיס המז'רדן משמאל לימין. שימו לב שסדר הוקטורים בבסיס המז'רדן חשוב מאד.
- השלב הבא הוא להשלים את הבסיס שמצאנו (
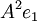 ) לבסיס למרחב
) לבסיס למרחב 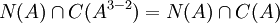 מהצורה
מהצורה 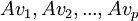 באופן הבא:
באופן הבא:
- נבחר בסיס
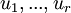 למרחב העמודות
למרחב העמודות 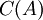
- נפתור את המערכת
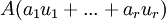 על מנת למצוא בסיס ל
על מנת למצוא בסיס ל 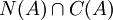
- נשמיט וקטורים על מנת שלא תהא תלות לינארית בבסיס שבחרנו עד כה
- נבחר בסיס
בדוגמא שלנו, העמודה הראשונה, השנייה והחמישית מהוות בסיס למרחב העמודות של A:
כעת נפתור את המערכת 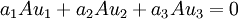 , זהו בדיוק מרחב האפס של המטריצה שעמודותיה הן
, זהו בדיוק מרחב האפס של המטריצה שעמודותיה הן 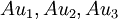 :
:
כיוון שאלו המקדמים 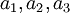 אנו מקבלים את בסיס ל
אנו מקבלים את בסיס ל 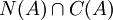 :
:
הערה: שימו לב ש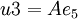 כיוון שזו העמודה החמישית
כיוון שזו העמודה החמישית
כיוון ש 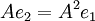 אנו משמטים איבר זה ונשארים עם
אנו משמטים איבר זה ונשארים עם 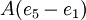
- המסלול
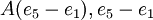 משלים לנו את הבסיס המז'רדן.
משלים לנו את הבסיס המז'רדן.
סיכום
הבסיס המז'רדן הינו
נסמן בP את המטריצה שעמודותיה הן איברי הבסיס
אזי (לא במפתיע) מתקיימת המשוואה הבאה:
כלומר זו צורת הז'ורדן של המטריצה A.
ז'ירדון של מטריצה עם ע"ע יחיד
מצאו בסיס מז'רדן למטריצה הבאה:
- ראשית נמצא את הפולינום האופייני
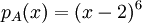 , כלומר 2 הינו הערך העצמי היחיד
, כלומר 2 הינו הערך העצמי היחיד
- לפי משפט קיילי המילטון
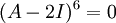 ולכן
ולכן 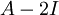 ניליפוטנטית.
ניליפוטנטית.
- נמצא לה צורת ז'ורדן
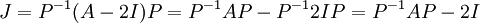
- לכן צורת הז'ורדן של המטריצה A הינה
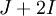 , כאשר הבסיס המז'רדן הוא אותו בסיס המז'רדן את
, כאשר הבסיס המז'רדן הוא אותו בסיס המז'רדן את 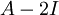 .
.
- כעת
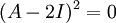 , לכן נמצא בסיס ל
, לכן נמצא בסיס ל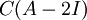
- העמודה הראשונה, השנייה והחמישית פורסות את מרחב העמודות של המטריצה ולכן הבסיס הינו
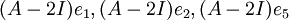
- בסיס זה מייצר שלושה מסלולים מאורך שתים, ולכן מצאנו מיד בסיס מז'רדן:
ושוב, הפלא ופלא, מתקיים: