שיחה:89-113 תשעג סמסטר ב
תוכן עניינים
- 1 הוספת שאלה חדשה
- 2 שאלות
- 2.1 דף 1-תרגיל 3
- 2.2 תרגיל 2
- 2.3 R2[x]
- 2.4 בהמשך לשאלה הקודמת
- 2.5 שאלה 2 בתרגיל 2
- 2.6 שאלה 1 תרגיל 3
- 2.7 שאלה 1 תרגיל 3
- 2.8 שאלה לגבי ערכים עצמיים ווקטורים עצמיים
- 2.9 ו"ע, ע"ע
- 2.10 שאלה
- 2.11 אם U תת-מרחב של V ומתקיים dimU=dimV. האם ניתן להסיק מכך ש-U=V? אם כן, מדוע?
- 2.12 תרגיל 5 שאלה 4
- 2.13 דמיון מטריצות
- 2.14 תרגיל 5 שאלה 4
- 2.15 שאלה בקשר לסימן v שפרושו "או", לסימן U שפרושו "איחוד"
- 2.16 פולינום מינימלי להעתקה לינארית
- 2.17 פולינום אופייני ופולינום מינימלי.
- 2.18 פולינום מיניחמלי
- 2.19 מימדים
- 2.20 תרגיל 7 שאלה 2
- 2.21 תרגיל 7 שאלה 3
- 2.22 שתיי שאלות
- 2.23 שאלה בקשר לתרגול 7 עמוד 3, התרגיל בתחתית העמוד.
- 2.24 צורות ז'ורדן
- 2.25 שאלה כללית
- 2.26 להגיד "A לכסינה" ולהגיד "A דומה למטריצה אלכסונית" זה אותו דבר?
- 2.27 תרגיל 7 שאלה 7
- 2.28 שילוש מטריצה
- 2.29 2 שאלות
- 2.30 שאלה כללית
- 2.31 איך מוכיחים שאיברי האלכסון של מטריצה משולשית הם הערכים העצמיים שלה?
- 2.32 אם מתקיים A(A-I)=0, למה זה אומר שהפ"א הוא x(x-1)?
- 2.33 תרגיל 9 שאלה 5 סעיף א'
- 2.34 שאלה 5 סעיף ב'
- 2.35 אם יש לי שניי בסיסים B1 ו-B2 למרחב וקטורי V ואני רוצה למצוא את מטריצת המעבר מבסיס אחד לבסיס השני. איך עושים את זה?
- 2.36 לגבי תרגיל מספר 3, שאלה 1
- 2.37 לגבי השאלה של מציאת מטריצת מעבר מבסיס אחד לשני
- 2.38 כמה שאלות לגבי תרגיל 5
- 2.39 שאלה לגבי המשפט: תהי T ט"ל של מרחב לינארי ממימד n. אם ל-T יש n ע"ע שונים, אז T לכסינה
- 2.40 מהם הדרכים למצוא ר"ג של ע"ע ומה הדרך הקצרה ביותר?
- 2.41 מה בדיוק השיטה למציאת מטריצה מלכסנת P, ולמציאת מטריצה אלכסונית?
- 2.42 תמיד אפשר למצוא מטריצה הפוכה למטריצה A ע"י קיילי-המילטון?
- 2.43 בקשר לפתרון של שאלה 5 בתרגיל 6.
- 2.44 תרגיל 6 שאלה 6
- 2.45 כמה שאלות
- 2.46 שאלה בקשר העמוד הראשון בתרגול מספר 7
- 2.47 שאלה בקשר למציאת בסיס לkerT בהינתן מטריצה מייצגת של T
- 2.48 מה זה היטל אורתוגונלי? האם צריך להכיר את המושג הזה?
- 2.49 תרגיל 9 שאלה 2 סעיף ב'
- 2.50 שאלה
- 2.51 בהינתן פולינום ב-
- 2.52 תרגיל 10 שאלה 7
- 2.53 מציאת פ"מ
הוספת שאלה חדשה
הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).
-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן
אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.
שאלות
דף 1-תרגיל 3
בשיעורי הבית, בתרגיל 3, יש אזהרה די מלחיצה שאומרת "ניקוד חלקי בלבד יינתן לחישוב ארוך מהדרוש" ניסיתי להבין לאיזה שיטה ניסיתם לרמוז לנו להשתמש בהתחלה דרגתי את המטריצה וקיוויתי להגיע לשורת אפסים וכו', אבל ראיתי שאני מתבחבש וחשבתי שזו לא הדרך פתרתי את השאלה ע"י הוספת שתי העמודות הראשונות מימין למטריצה - ואז חישוב סכום האלכסונים הראשיים פחות סכום האלכסונים המשניים (שיטה שראינו בתרגול בסמסטר הקודם , ומותר לעשות אותה כי מדובר במטריצה 3x3). האם שיטה זו נחשבת לחישוב הארוך המיותר, שרמזתם לו?
אשמח להבהרה בנושא
>>תנסה ע"י חיסור רק לבטל איקסים בשתי שורות(או עמודות), להפוך את החישוב לבעל פחות משתנים.
עדי
תרגיל 2
בשאלה 4 האם מספיק לרשום את העתקה שמצאתי או שעליי להוכיח שהיא גם לינארית?
>> לא צריך להוכיח לינאריות, רק למצוא את ההעתקה, כולל דרך מלאה למציאתה. עדי
R2[x]
זו מרחב הפולינומים מהצורה ax^2+bx+c? בבסיס של המרחב הזה יש 3 וקטורים?
תודה וחג שמח
כן. עדי
בהמשך לשאלה הקודמת
אם אני רוצה להוכיח ש
1
1+x
1+x+x^2
מהווה בסיס ל-R2[x], מספיק לי להוכיח שזו קבוצה בת"ל? או שנאי צריך להוכיח גם שהיא פורשת?
תודה
היות ומדובר ב-3 וקטורים מספיק להוכיח בת"ל, ולתת נימוק למה זה מספיק. עדי
שאלה 2 בתרגיל 2
אני רוצה לבדוק ש-T לינארית כאשר C מ"ו מעל C. לשם כך אני צריך לבדוק שמתקיים: T(v1+v2)=T(v1)+T(v2)
וגם
T(alfa*v)=alfaT(v)
יש לי 2 שאלות:
ההבדל בין מ"ו C מעל C לבין מ"ו C מעל R מתבטא בדרישה השנייה בלבד?
כלומר במקרה של "מעל C", alfa יהיה מרוכב ובמקרה של מעל R alfa יהיה ממשי?
כן, ההבדל הוא בסקלרים. הוקטורים, היות ומוגדרים מעל C בשני המיקרים, ישארו מרוכבים. (באופן כללי,הרלוונטיות של "מעל F" היא כבר בהגדרה של המרחב הוקטורי, עוד לפני ההעתקה) עדי
ושאלה שנייה:
כשאני בודק אם T(alfa*v)=alfa*T(v)
במקרה ששואלים אם T לינארית כאשר C מ"ו מעל C, מה ההבדל בין v לבין alfa? יש הבדל בין סקלר מרוכב לווקטור מרוכב?
במקרה זה אין הבדל, היות והמרחב הוקטורי הוא השדה עצמו, אך זהו מקרה פרטי. וקטור מרוכב גם יכול להגיע מ ![C^n,\ C^{nxn},C_n[x]](/images/math/d/9/a/d9a2f77acd376e7a2eb3910e0c9a7c82.png) וכו', אז יש הבדל בין השניים. עדי
וכו', אז יש הבדל בין השניים. עדי
תודה.
שאלה 1 תרגיל 3
למה V-->F^m העתקה לינארית? (m המימד של V)?
תודה
אני לא מבינה על איזו ה"ל מדובר, אין ה"ל בשאלה זו. עדי
שאלה 1 תרגיל 3
אם אני יודע ש:
![a_1v_1+a_2v_2+....+a_nv_n=0 <=> a_1[v_1]_B+...+a_n[v_n]_B=0](/images/math/d/6/1/d61467c5a0089a70b6355e9bb15db310.png) ,
,
B בסיס של מ"ו V,
אז אני יכול לומר שזה שקול ללהגיד:
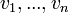 בת"ל <=>
בת"ל <=> ![[v_1]_B,...,[v_n]_B](/images/math/8/2/9/829af11b57fda12960a03547d8fcb229.png) בת"ל?
בת"ל?
אם כן , למה? אם לא, מה חסר לי בשביל להסיק את השורה האחרונה?
תודה!
ראשית, הוספתי כמה תיקונים בניסוח המקורי לפי מה שנראה לי שהיתה כוונתך, מקווה שזה תקין.
שנית, אם אכן לזאת הכוונה בשאלה, התשובה היא: כמעט. חסר לך המעבר מ-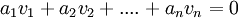 להיותם של
להיותם של 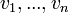 בת"ל, והוא:
בת"ל, והוא: 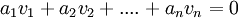 רק כאשר
רק כאשר 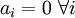 .
.
כלומר, אם תוכיח ש-
![(a_1v_1+a_2v_2+....+a_nv_n=0=>a_i=0\ \forall i)<=>(
b_1[v_1]_B+...+b_n[v_n]_B=0=>b_i=0\ \forall i)](/images/math/4/4/f/44f59313d4bcc35fd8c721f42388eda2.png)
אז תוכל להסיק 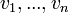 בת"ל <=>
בת"ל <=> ![v_1]_B,...,[v_n]_B]](/images/math/2/3/f/23f954f6611c5150bc6b1f784499d213.png) בת"ל.
בת"ל.
לדוגמא עבור אחד הכיוונים: נניח שצירוף לינארי של 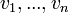 מתאפס רק כאשר כל מקדם מתאפס. ניקח
מתאפס רק כאשר כל מקדם מתאפס. ניקח ![a_1[v_1]_B+...+a_n[v_n]_B=0](/images/math/9/4/8/948a482674b5b1e94f7c4e15c0cb9469.png) ונקווה לגלות ע"ס ההנחה שכל מקדם מתאפס. כנ"ל בכיוון ההפוך.
ונקווה לגלות ע"ס ההנחה שכל מקדם מתאפס. כנ"ל בכיוון ההפוך.
יתכן שהתכוונת בשורה הראשונה שצירוף לינארי לא טריו' מתאפס אמ"מ... ואז האחד ת"ל אמ"מ השני ת"ל ולכן האחד בת"ל אמ"מ השני בת"ל, אבל חשוב לציין שזה צירוף לא טריויאלי ושזה גורר תלות לינארית ולא אי תלות לינארית.
עדי
שאלה לגבי ערכים עצמיים ווקטורים עצמיים
למה כאשר מוצאים וקטורים עצמיים עבור ע"ע, יתקבל תמיד מרחב? כלומר למה יש אינסוף וקטורים עצמיים, עבור ערך עצמי מסוים?
תודה מראש.
מכיוון שעבור כל וקטור עצמי v עם ע"ע x וסקלר a:
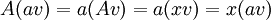 ולכן גם av הוא ו"ע של אותו ע"ע.
ולכן גם av הוא ו"ע של אותו ע"ע.
באופן כללי עבור 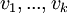 ו"ע שהתקבלו עבור ע"ע x וסקלרים
ו"ע שהתקבלו עבור ע"ע x וסקלרים 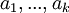 :
:
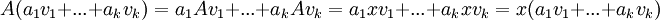
ולכן גם 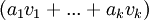 (הצירוף הלינארי שלהם) הוא ו"ע של אותו ע"ע.
(הצירוף הלינארי שלהם) הוא ו"ע של אותו ע"ע.
עדי
ו"ע, ע"ע
אם מצאתי ע"ע כלשהו ואז מצאתי את המרחב העצמי המתאים לו וקבלתי שהמרחב הזה הוא מהצורה
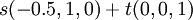
כאשר t,s ממשיים.
האם אני יכול לומר שהמרחב העצמי הזה שקול למרחב העצמי מהצורה s(1,-2,0)+t(0,0,1) כלומר הכפלתי את הוקטור (0.5,1,0-) ב-2-.
האם מותר לי לעשות את זה? אם כן, למה? אני לא צריך להכפיל את שניי הוקטורים ב2-?..שוב, אם כן, למה..
תודה מראש
>>כל מה שנפרש ע"י וקטור בודד הוא מכפלה שלו בסקלר (כלומר "מתיחה וכיווץ" שלו), ולכן כל מה שנפרש ע"י v שקול לחלוטין למה שנפרש ע"י av עבור סקלר מהשדה מעליו מוגדר המרחב.
לכן, מרחב וקטורי הנפרש ע"י n וקטורים, נפרש גם ע"י כל מכפלה שלהם בסקלרים:
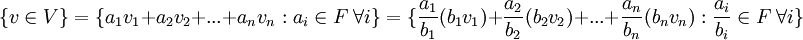
גם 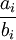 הם כל הסקלרים האפשריים ב-F מכיוון ש-F שדה:
הם כל הסקלרים האפשריים ב-F מכיוון ש-F שדה: 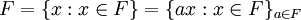 .
.
כלומר המרחב אינו שקול, הוא ממש שווה.
בדוגמא שנתת הצירוף הלינארי 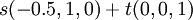 , עבור כל סקלר s מהשדה, שווה ל-
, עבור כל סקלר s מהשדה, שווה ל-
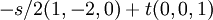 , עבור כל סקלר
, עבור כל סקלר 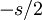 מהשדה.
מהשדה.
באשר לתפקידם כוקטורים עצמיים, ראה שאלה קודמת.
עדי
שאלה
להגיד שקבוצה היא לא פורשת מינימלית או להגיד שקבוצה היא תלויה לינארית זה טיעונים שקולים? או שבכלל אין קשר בין הטיעונים?
>>כן, אך מצריך נימוק הולם. בכל מקרה ע"מ להימנע מכפל משמעויות יש לומר "פורשת לא מינימלית", שיבינו שהיא"פורשת" אבל "לא מינימלית", ולא "לא פורשת".
עדי
אם U תת-מרחב של V ומתקיים dimU=dimV. האם ניתן להסיק מכך ש-U=V? אם כן, מדוע?
אם U תת-מרחב של V ומתקיים dimU=dimV. האם ניתן להסיק מכך ש-U=V? אם כן, מדוע?
(לא מתרגל): בסיס במרחב U הוא קבוצה בת"ל בV, וידוע כי מס' האיברים בבסיס של U שווה למימד של V. נקבל שזה בסיס לפי השלישי חינם.
תרגיל 5 שאלה 4
כשמבקשים להוכיח ש I-T איזומורפיזם...איך אפשר להחסיר את T מ-I? T זו ה"ל ו-I זו מטריצה..לא הבנתי את השאלה הזו..
>> בהקשר של ה"ל 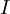 היא העתקת הזהות, כלומר
היא העתקת הזהות, כלומר 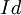 .
.
עדי
דמיון מטריצות
אם למטריצות יש פולינום אופייני זהה/דטרמיננטה שווה/עקבה שווה זו הוכחה מספקת לדימיון?
או שהדרך היחידה להוכחה היא למצוא P שמקיימת:
A=P^-1 B P
>>אין זה מעיד על דמיון. מה עם מטריצות בעלות פ"א זהה, האחת לכסינה והשניה לא? למשל
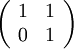 ומטריצת הזהות, הן לא יהיו דומות. עדי
ומטריצת הזהות, הן לא יהיו דומות. עדי
תרגיל 5 שאלה 4
T^3(v)=0? זה הנתון?
בין האפס ל-T^3 לא רשום כלום...רק רציתי לוודא
>> כאשר אומרים על פונקציה 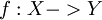 שהיא שווה לאפס: f=0 (או אפס זהותית), הכוונה שהפונקציה שולחת כל איבר בתחום לאפס. כלומר
שהיא שווה לאפס: f=0 (או אפס זהותית), הכוונה שהפונקציה שולחת כל איבר בתחום לאפס. כלומר 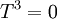 אומר
אומר 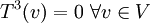 . עדי
. עדי
שאלה בקשר לסימן v שפרושו "או", לסימן U שפרושו "איחוד"
האמת שהשאלה קצת יותר קשורה לבדידה אבל היא רלוונטית לכל קורס במתמטיקה..
אם A,B קבוצות, אז להגיד AVB זה כמו להגיד AUB? אם כן, למה?
הקשר הבינארי "או" הוא לוגי והוא מבטא פסוק שהוא אמת כאשר לפחות אחד משני מרכיביו הוא אמת. (כלומר הסימון AVB עבור A ו-B קבוצות איננו תקין, כי קבוצה לא יכולה להיות אמת או שקר. למשל הפסוק "הקבוצה ריקה" יכול להיות אמת או שקר, לכן "הקבוצה ריקה או הקבוצה איננה ריקה" הוא בהכרח פסוק אמת כי לפחות אחד ממרכיביו אמת).
הפעולה הבינארית "איחוד" היא מתורת הקבוצות והיא מתארת את צירופן של שתי קבוצות לכדי קבוצה חדשה.
על כן, ניתן לקשר בין שני סימנים אלו ע"י מעבר לשייכות לקבוצות: 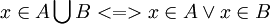
באותו אופן הקשר בין "חיתוך" ל"וגם" הינו: 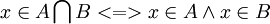 .
.
עדי
פולינום מינימלי להעתקה לינארית
בתרגיל 7 שאנחנו צריכים להגיש יש למצוא פולינום מינימלי עבור העתקה לינארית , על פי מה שלמדנו אני יודע למצוא פולינום מינימלי עבור מטריצה A מסויימת אבל איך אני אמור למצוא פולינום מינימלי עבור העתקה לינארית? אצ יכולה לתת לי סכמת פיתרון למצבים מבוקשים כאלה <?
>> ככל אנלוגיה שראינו בין מטריצות להעתקות לינאריות, כך גם עבור הפ"א:
![f_T=f_{[T]}](/images/math/4/a/f/4afbe041a190d953514b1c22b3e3e2e9.png) כאשר [T] היא מט' מייצגת של T (הפ"א לא יהיה תלוי בבחירת הבסיס).
כאשר [T] היא מט' מייצגת של T (הפ"א לא יהיה תלוי בבחירת הבסיס).
ובאותו אופן הפ"מ יהיה המתוקן המינימלי שמאפס את [T]. עדי
פולינום אופייני ופולינום מינימלי.
למה הפולינום המינימלי מחלק את הפולינום האופייני?
תודה.
>> חלוקת פולינומים ללא שארית נעשית באופן אנאלוגי לחלוקה ללא שארית של מספרים שלמים, נזכיר:
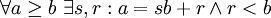 כלומר ניתן להציג את a ככפולות שלמות של b ועוד שארית קטנה מ-b (אחרת ניתן לקחת s גדול יותר). ואז
כלומר ניתן להציג את a ככפולות שלמות של b ועוד שארית קטנה מ-b (אחרת ניתן לקחת s גדול יותר). ואז  , כלומר כשהשארית מתאפסת.
, כלומר כשהשארית מתאפסת.
עבור פולינומים:
![\forall f,g\in F[x]: deg(f)\geq deg(g)\ \exists s,r\in F[x]:f(x)=s(x)g(x)+r(x) \and deg(r)<deg(g)](/images/math/b/7/5/b75ffda6125979f35e33f3cb6ecc51f5.png) .
.
ידוע שדרגת הפ"מ קטנה מדרגת הפ"א לכן ![\exists s,r\in F[x]:f_A(x)=s(x)M_A(x)+r(x) \and deg(r)<deg(M_A)](/images/math/a/2/b/a2b26bced41c6adb058edfc4472bd262.png) .
.
נציב A, נשתמש במשפט קיילי המילטון ונקבל:
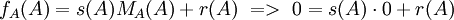 , כלומר, r גם מאפס את A. אבל הפולינום היחיד שמאפס את A אשר דרגתו קטנה מזו של הפ"מ (כנדרש עבור פולינום השארית r) הוא פולינום האפס, לכן
, כלומר, r גם מאפס את A. אבל הפולינום היחיד שמאפס את A אשר דרגתו קטנה מזו של הפ"מ (כנדרש עבור פולינום השארית r) הוא פולינום האפס, לכן 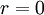 ו-
ו-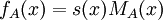 כנדרש.
כנדרש.
(האמת, שהוכחה זו תקפה לכל פולינום שמאפס את A, לכן ציינו שהמינימלי מחלק כל פולינום כזה. מה שנכון בנוסף לכך לפולינום האופייני הוא שכל גורמיו האי פריקים יהיו במינימלי. למשל הפולינום x מחלק את 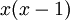 , אבל אין לו את כל חלקיו האי פריקים. בין הפ"א לפ"מ יש בדיוק את אותם חלקים אי פריקים, החזקות במינימלי עלולות להיות נמוכות יותר. הסיבה לתכונה זו היא ש
, אבל אין לו את כל חלקיו האי פריקים. בין הפ"א לפ"מ יש בדיוק את אותם חלקים אי פריקים, החזקות במינימלי עלולות להיות נמוכות יותר. הסיבה לתכונה זו היא ש 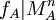 , אבל זו כבר הוכחה ארוכה יותר).
, אבל זו כבר הוכחה ארוכה יותר).
עדי
פולינום מיניחמלי
בסיכום של תרגול 7 מופיעה דוגמה למטריצה A מסדר 3x3 שכל איבריה הם 0.
הפולינום האופייני שלה הוא lamda^3-
רשום שהפולינום המינימלי הוא lamda.
הסבר: "זהו פולינום מתוקן מדרגה מינימלית ש-A מאפסת".
אני מבין למה הוא מתוקן ולמה הוא מדרגה מינימלית. מה שאני לא מבין זה למה A מאפסת אותו.
>> כי אם תציב A תקבל 0 (A=0). עדי
מימדים
אם U,V מרחבים וקטוריים ו-U מוכל ממש ב-V. האם זה גורר שהמימד של U קטן ממש מהמימד של V? אם כן, מדוע? תודה מראש.
>> כן. וודאי מימד U לא גדול ממימד V. נניח בשלילה שמימדיהם שווים והמימד הוא n. ניקח בסיס ל-U: 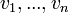 , אזי זו קבוצה בת n אייברים בת"ל ב-U ולכן זו קבוצה בת n אייברים בת"ל ב-V. היות ומימד V הוא n הרי שזו קב' בת"ל מגודל המימד ולכן בסיס ל-V. ולכן
, אזי זו קבוצה בת n אייברים בת"ל ב-U ולכן זו קבוצה בת n אייברים בת"ל ב-V. היות ומימד V הוא n הרי שזו קב' בת"ל מגודל המימד ולכן בסיס ל-V. ולכן 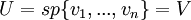 , סתירה.
באותו אופן, אם U מוכל ב-V ומימדיהם שווים U=V.
עדי
, סתירה.
באותו אופן, אם U מוכל ב-V ומימדיהם שווים U=V.
עדי
תרגיל 7 שאלה 2
שלום!
הראיתי שהפולינום האופייני של A הוא x^3-ax^2-bx-c אפשר כיוון לחלק השני של השאלה..? צריך להראות שזה גם הפולינום המינימלי. הפולינום האופייני הוא פולינום מתוקן...צריך לבדוק ש-A מאפסת אותו? זה נראה לי הרבה עבודה..יש דרך יורת אלגנטית? וחוץ מזה, גם אם הראיתי ש-A מאפסת אותו, איך אני יודע שהוא מדרגה מינימלית?
תודה מראש.
>> הפ"מ וודאי לא מדרגה אחת (חשוב ונמק למה), לכן אם לא האופייני הוא יכול להיות רק מדרגה 2. קח פולינום כללי מדרגה 2: 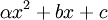 הצב בו את A והראה מדוע לא קיים כזה (כלומר, שפולינום כזה יתאפס רק כאשר כל מקדם הוא אפס). ההצבה די פשוטה, מספיקים לך 3 רכיבים במטריצה כדי לאפס 3 מקדמים. עדי
הצב בו את A והראה מדוע לא קיים כזה (כלומר, שפולינום כזה יתאפס רק כאשר כל מקדם הוא אפס). ההצבה די פשוטה, מספיקים לך 3 רכיבים במטריצה כדי לאפס 3 מקדמים. עדי
תרגיל 7 שאלה 3
הפולינום האופייני בטוח יוצא x^2(x-1)^2 ? יוצא לי משהו טיפה שונה..יכול להיות שיש שם טעות?
>> חישבתי עכשיו ויצא לי מה שרשום בתרגיל.
אגב, את שוויון הפ"א לפ"מ קל להראות במקרה זה דרך צורת הג'ורדן, (כלומר דרך הר"ג). ניתן למצוא מאוד בקלות את מרחב האפס של A ו-A-I, ולהסיק משם את החזקות ב-M (שהן גודל הבלוקים המקסימליים). עדי
שתיי שאלות
1.יש משפט בתרגול 7 לפיו אם מטריצות A,B דומות אז הפ"א זהה וגם הפ"מ זהה.
הכוונה שלכל אחת מהן בנפרד יש פ.מ ופ.א זהים? או שלשתיהן יש את אותו פ.א ואותו פ.מ?
>> הכוונה 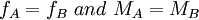
2. בתרגול 7 מופיעה הערה: מטריצה לכסינה <=>הפ.מ מתפרק לגורמים לינאריים שונים.
הטענה נכונה גם אם במקום פ.מ ארשום פ.א?
אם כן, מה הקטע פה? הרי בשביל למצוא פ.מ אני צריך למצוא קודם את הפ.א, אז אם הטענה נכונה עבור הפ.א זה כבר מספיק לי בשביל לדעת אם היא לכסינה.
תודה מראש.
>> המשפטים אומרים:
מטריצה היא לכסינה אמ"מ הפ"א מתפרק לגורמים לינארים (לא בהכרח שונים, למשל 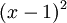 יכול להופיע) וגם כל ריבוי אלגברי שווה לריבוי הגיאומטרי המתאים לו.
יכול להופיע) וגם כל ריבוי אלגברי שווה לריבוי הגיאומטרי המתאים לו.
מטריצה היא לכסינה אמ"מ הפ"מ מתפרק לגורמים לינארים שונים (למשל, הגורם הלינארי ממקודם יהיה בהכרח 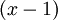 , כלומר אם החזקות של כל גורם פריק בפ"א ירדו ל-1). עדי
, כלומר אם החזקות של כל גורם פריק בפ"א ירדו ל-1). עדי
שאלה בקשר לתרגול 7 עמוד 3, התרגיל בתחתית העמוד.
לא הבנתי איך הגעת ל- g(x)=x^2-1 ולמה צריך את זה...
ועוד משהו...למה g(A)=0.
תודה מראש
>> מבקשים למצוא פ"א ופ"מ. ראשית ננסה להבין מהנתון איך נראים הפולינומים שמאפסים את A.
נתון A^2=I שזה אומר A^2-I=0, כלומר זה הביטוי שתקבל אם תציב A ב 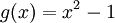 . הפ"מ מחלק כל פולינום שמאפס את A, ובפרט את g. מקווה שכעת יתר הפיתרון ברור. אם לא, מוזמן לשאול.
. הפ"מ מחלק כל פולינום שמאפס את A, ובפרט את g. מקווה שכעת יתר הפיתרון ברור. אם לא, מוזמן לשאול.
עדי
צורות ז'ורדן
אם נתון לי בלוק ז'ורדן מסדר k על k, מתקיים פ.א=פ.מ=x-lamda)^k) זה שהפ.א שווה לביטוי הזה, זה מובן לי. איך יודעים שגם הפ.מ שווה לביטוי הזה???
תודה מראש!
' לפי דרגת הנילפוטניות של 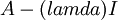 . עדי
. עדי
שאלה כללית
נניח נתון פולינום אופייני ואני רוצה למצוא את הפולינום המינימלי, והראיתי ש-A לא מאפסת אף אחד מהמחלקים של הפולינום האופייני, שוונים מהפולינום האופייני. מדוע אפשר להסיק מכך שהפולינום המינימלי הוא הפולינום האופייני?
אשמח לעזרה.
אם אף פולינום מדרגה נמוכה יותר לא מאפס אז הפ"א הוא הפולינום מהדרגה המינימלית שעושה זאת. עדי
להגיד "A לכסינה" ולהגיד "A דומה למטריצה אלכסונית" זה אותו דבר?
תודה
כן, עבור מטריצה. עבור ה"ל זה אומר שקיים בסיס כך שהמט' המייצגת אלכסונית, וניתן להוכיח שמספיק לדרוש שהמט' המייצגת לכסינה. עדי
תרגיל 7 שאלה 7
בסעיף b, מבקשים למצוא פ"מ של T.
באופן כללי, אם מבקשים ממני למצוא פ"מ/פ"א, הכוונה היא ביחס למטריצה, לא?
כאן נתונה העתקה לינארית T. אין כאן בכלל מטריצה...מה אני צריך לעשות???
ראה למעלה דיון פ"מ לה"ל. עדי
שילוש מטריצה
לא ממש הבנתי בחלק של תרגול 8 בעמוד 3 איך יודעים מי זו המטריצה C. אשמח לעזרה..תודה.
ומי זו בדיוק המטריצה k על k בעמוד 2 בתרגול 8?
אתה מתכוון לאלגוריתם או לדוגמא? (כמו כן, מה מופיע אצלך כ-C? המשלשת?)
בעקרון אני לא מבין גם באלגוריתם וגם בדוגמה איך יודעים מי זו בדיוק המט' C הזו ומי זו המט' k על k.
ומה מציינת כל אחת מהמטריצות.
לא הבנתי גם איך יודעים שמתחת ומעל לאלכסון שבמט' kxk יש אפסים ואיך יודעים שמתחת למט' kxk ומשמאל למט' C יש אפסים?
ב-C (בדוגמה בעמוד 3) מופיע לי בשורה הראשונה 3 ו-1 ובשורה השנייה 1- ו-1
רשום שעל המט' C נעשה את אותו תהליך. למה דווקא עליה?..זאת אומרת, איך יודעים מי זו המטריצה שעליה עושים את אותו תהליך?
לא בטוחה מאיפה המערך שאתה מדבר עליו, אתם נותנים פה הפניות למספרי עמודים אבל זו הגירסה של המתרגל/מתרגלת שלך וכמו כן לא כל הקבוצות מקבלות העתק שלו. אז להבא רצוי לומר על איזו הגדרה/טענה/דוגמא מדובר ולא עמוד.
הקלדתי את האלגוריתם והדוגמא במפורט (מומלץ לכולם):
עדי
2 שאלות
שלום,
בתרגול 8 בעמוד 6, רשום שעבור למדה=1, ר"ג=2 (לכן יש 2 בלוקים)
איך מגיעים לכך שהר"ג=2?
תודה
מכך שמימד המ"ע (כלומר מרחב האפס של 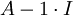 ) הוא 2. עדי
) הוא 2. עדי
שאלה כללית
אני יודע שכל מטריצה A שהפולינום האופייני שלה מתפרק לגורמים לינאריים דומה למטריצה בצורת ז'ורדן. השאלה שלי היא האם היא דומה למטריצה יחידה בצורת ז'ורדן.
כן, למטריצה צורת ג'ורדן אחת ויחידה, אם כי לא תמיד יש לנו מספיק נתונים כדי לדעת אותה. שים לב להוראה "מצא את צורת ג'ורדן" או "מצא את כל צורות ג'ורדן האפשריות". עדי
איך מוכיחים שאיברי האלכסון של מטריצה משולשית הם הערכים העצמיים שלה?
אה..בעצם מה העניין פה? זה מיידי לא? אם עושים דטרמיננטה של כפולה של מטריצת היחידה בסקלר, פחות המטריצה המשולשית, אז מקבלים דטרמיננטה של מטריצה משולשית. לכן הפולינום האופייני הוא מכפלת איברי האלכסון והערכים העצמיים יהיו איברי האלכסון של המטריצה המקורית?
איך אבל יודעים שאלו כל הערכים העצמיים ושאין עוד מלבדם?
הנימוק שציינת הוא הסיבה לכך ששורשי הפולינום האופייני על האלכסון. הסיבה לכך ששורשי הפולינום האופייני הם הע"ע ולהיפך היא: שורשים מאפסים את 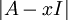 אם ורק אם הם הופכים את A-xI לה"ל/מטריצה לא הפיכה אם ורק אם קיימים להם וקטורים לא אפסיים כך ש- Av=xv. עדי
אם ורק אם הם הופכים את A-xI לה"ל/מטריצה לא הפיכה אם ורק אם קיימים להם וקטורים לא אפסיים כך ש- Av=xv. עדי
אם מתקיים A(A-I)=0, למה זה אומר שהפ"א הוא x(x-1)?
?
>> מה סדר המטריצה?
זה רק אומר שהפ"מ מחלק את 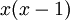 כי הוא מחלק כל פולינום שמאפס את A. כלומר הפ"מ הוא x או x-1 או
כי הוא מחלק כל פולינום שמאפס את A. כלומר הפ"מ הוא x או x-1 או 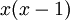 . עדי
. עדי
תרגיל 9 שאלה 5 סעיף א'
אני מפתח את אגף ימין במטרה להגיע לאגף שמאל וכך בעצם להוכיח את הטענה. במהלך הפיתוח, יש מצב מסוים שבו אני רוצה להשתמש בלינאריות במשתנה השני. על מנת לעשות זאת ללא שימוש בצמודים המרחב V צריך להיות R^n???
>> לא בהכרח, מספיק שהוא יהיה מעל R (כלומר ![...,R^n,R_n[x],M_n(R)](/images/math/9/6/1/96148b30308cd9cf8ec9fecea4fc10a6.png) וכו') כפי שאכן מוגדר בסעיף זה. עדי
וכו') כפי שאכן מוגדר בסעיף זה. עדי
שאלה 5 סעיף ב'
בתוך הסוגריים שבאגף ימין, יש 4 מחוברים. השניים הראשונים הם
2^||u+v|| פחות 2^||u-v||
בסעיף א' מצאנו שכאשר כופלים את שניי הביטויים הללו ברבע הם שווים ל
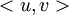 .
.
השאלה היא האם מותר להחליף את המכפלה שלהם ברבע, בתוצאה שקיבלנו בסעיף א' העניין הוא שבסעיף א' היה מעבר אחד של לינאריות ברכיב השני שהסתמך על כך שזה R ולא C
>>ענית לעצמך. לא ניתן להשתמש בסעיף א' כיוון שפיתוח הסעיפים שונה מעל C ומעל R. עדי
אם יש לי שניי בסיסים B1 ו-B2 למרחב וקטורי V ואני רוצה למצוא את מטריצת המעבר מבסיס אחד לבסיס השני. איך עושים את זה?
תודה מראש.
![B_1=\{v_1,...,v_n\} => [I]^{B_1}_{B_2}=\left([v_1]_{B_2}\cdots [v_n]_{B_2}\right)](/images/math/3/6/2/36246b15a9f67b138f7243d6944a0f06.png) , כאשר
, כאשר ![[v_i]_{B_2}](/images/math/4/e/5/4e5e04dd2cbdc79d04c2684e7b90f722.png) הוא וקטור הקואורדינטות של
הוא וקטור הקואורדינטות של 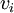 לפי
לפי 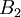 . עדי
. עדי
לגבי תרגיל מספר 3, שאלה 1
בתחילת הפתרון רשום שקל לוודא
![[\ ]:V->F^m](/images/math/b/e/9/be9d13bb60989e3859cbd3033a283ff9.png) היא העתקה לינארית לפי הקריטריון המקוצר.
היא העתקה לינארית לפי הקריטריון המקוצר.
לא הבנתי על איזה העתקה מדובר...איזה העתקה בכלל נתונה בשאלה הזו. ולא הבנתי איך אני מוודא את זה לפי הקריטריון המקוצר...וגם מזה בכלל הקריטריון המקוצר. תודה..
>>בחרנו בהעתקה ![[\ ]_B:V->F^m](/images/math/b/e/f/befb1e289b975bfe06f021f135c8a538.png) (הכוונה להעתקה שלוקחת וקטור במרחב ומחזירה את וקטור הקואורדינטות שלו). והיא לינארית לפי הקריטריון המקוצר, שהוא:
(הכוונה להעתקה שלוקחת וקטור במרחב ומחזירה את וקטור הקואורדינטות שלו). והיא לינארית לפי הקריטריון המקוצר, שהוא:
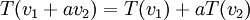 . עדי
. עדי
לגבי השאלה של מציאת מטריצת מעבר מבסיס אחד לשני
לא הבנתי מאיפה הגיע הסימון I, איך קשורה כאן העתקת הזהות??
>> למעשה מטריצת מעבר היא מקרה פרטי של מטריצה מייצגת כאשר T=I. מטריצת המעבר מתקבלת (ע"פ הגדרה) ע"י החישוב ![\left([v_1]_{B_2}\cdots [v_n]_{B_2}\right)](/images/math/f/e/7/fe742a32edabf5a1ed46cbec05466b9b.png) שהוא בעצם
שהוא בעצם ![\left([I(v_1)]_{B_2}\cdots [I(v_n)]_{B_2}\right)](/images/math/0/f/3/0f35ed6e42972be93179edc9fa07ca88.png) שהיא בדיוק המטריצה המייצגת של I מהבסיס הראשון לשני, זו הסיבה שבחרו לתת לה את סימון זה. עדי
שהיא בדיוק המטריצה המייצגת של I מהבסיס הראשון לשני, זו הסיבה שבחרו לתת לה את סימון זה. עדי
כמה שאלות לגבי תרגיל 5
לגבי שאלה 1ג': איך יכול להיות מצב שT(v1),...,T(vn) לא שונים? הרי נתון שזה בסיס!
צודק. יתוקן
לגבי שאלה 4א':
בשלב שבו מנסים להראות ש-I-T חח"ע, לוקחים וקטור כלשהו ב-V כך ש- I-T)v=0). השאלה שלי היא איך יודעים שבהכרח קיים וקטור v שמקיים I-T)v=0) ?
כי קיים וקטור האפס שנשלח ל-0. בשביל חח"ע נרצה לבדוק אם זה קורה עבוק וקטור נוסף
לגבי שאלה 4ב': כאשר מגיעים לכך ש alfaT^2(v)=0 כתוב ש-T^2(v) שונה מאפס ולכן alfa=0.
מצד שני, נתון שקיים (כלומר לא לכל v!...פשוט קיים v כלשהו) וקטור v שונה מאפס ששייך ל-V המקיים T^2(v) שונה מאפס. איך יודעים שכאשר אומרים ש-T^2(v) שונה מאפס, מדובר על הוקטור הספציפי v ששונה מאפס?
בדיוק כמו קודם כי אם v=0 אל לכל ה"ל Tv=0
לגבי שאלה 5:
כאן יש לי כמה שאלות:
1. הקבוצה {קוסינוס טטא, סינוס טטא} מהווה בסיס ל-V. למה??? איך יודעים זאת?
כי כל וקטור ב-V הוא צירוף לינארי שלהם והם בת"ל (כשתאפס את הצ"ל, תציב פעם 0 ופעם 90 בזוית).
2. המטריצה המייצגת שמופיעה שם בפתרון...למה זו המטריצה המייצגת? ביחס לאיזה בסיסים היא? (התחום והטווח שונים..מה הבסיס של התחום ומה הבסיס של הטווח שביחס אליהם מוגדרת המטריצה הזו?
בסיס התחום הוא זה שמוגדרת עליו הה"ל: cos, sin בסיס הטווח הוא זה שהה"ל נשלחת אליו: 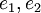 . ולכן זו המט' המייצגת
. ולכן זו המט' המייצגת
3. רשום "תזכורת: התמונה של העתקה נפרשת ע"י העמודות". העמודות הן לא ווקטורי הקוארדינטות של תמונות ווקטורי הבסיס, ביחס לבסיס של הטווח?
הכוונה לאנאלוגיה בין ה"ל למטריצות ע"י מבט על תמונה כמרחב העמודות וגרעין כמרחב האפס:
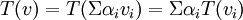 (שהוא צירוף לינארי של תמונות הבסיס) שקול ל-
(שהוא צירוף לינארי של תמונות הבסיס) שקול ל-
![[T]_C^B[v]_B=[Tv]_C](/images/math/f/5/5/f55b0230a9d227de79004abb3c264b69.png)
עדי
אשמח לעזרה! תודה מראש
שאלה לגבי המשפט: תהי T ט"ל של מרחב לינארי ממימד n. אם ל-T יש n ע"ע שונים, אז T לכסינה
שתיי שאלות למעשה:
1. מה הגירסא של המשפט עבור מטריצות
2. מדוע זה שיש גירסא עבור ט"ל גורר שיש גירסא עובר מטריצות, ולהיפך?
תודה מראש.
1. A מטריצה nxn. אם ל-A יש n ע"ע שונים, אז A לכסינה
2. כי ע"ע של T הם שורשי הפ"א של T שהוא הפ"א של [T], וממילא זה יגרור שיוויון ריבויים ולכן לכסינות
אולי השאלה היא בעצם למה לכסינות של ה"ל שקולה ללכסינות של מטריצה:
T לכסינה אמ"מ קיים בסיס B כך ש- ![[T]_B](/images/math/a/b/1/ab1448b9fd8f9741cf06687c08884c4f.png) אלכסונית
אלכסונית
A לכסינה אמ"מ היא דומה לאלכסונית
כלומר לה"ל אנחנו דורשים אלכסונית ולמטריצות רק דימיון לאלכסונית. מדוע זה שקול?
אם קיים בסיס B כך ש- ![[T]_B](/images/math/a/b/1/ab1448b9fd8f9741cf06687c08884c4f.png) אלכסונית אז לכל בסיס אחר C מתקיים
אלכסונית אז לכל בסיס אחר C מתקיים
![[T]_C=[T]^C_B[T]_B[T]^B_C](/images/math/8/3/c/83cb5474ea0ee3e6b11e3c64b0098860.png) , נגדיר
, נגדיר ![[T]^C_B=P](/images/math/d/a/8/da8ea99a9b1d7a6c78d4af8cbddbaaae.png) והרי ש-
והרי ש-
![[T]_C=P[T]_BP^{-1}](/images/math/2/2/4/22483a6ca3c4af6d104f976398d55420.png) . כלומר, לכל בסיס
. כלומר, לכל בסיס ![[T]_C](/images/math/1/d/2/1d2fa7b57ca1238f2af3faef3e7e2ccc.png) דומה לאלכסונית.
דומה לאלכסונית.
ז"א, מספיק לדרוש אלכסוניות כה"ל לבסיס אחד כדי לקבל לכסינות כמטריצה לכל בסיס.
עדי
מהם הדרכים למצוא ר"ג של ע"ע ומה הדרך הקצרה ביותר?
מהם הדרכים למצוא ר"ג של ע"ע  ומה הדרך הקצרה ביותר?
ומה הדרך הקצרה ביותר?
באופן כללי, לחשב את מרחב האפס של 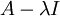
יש כל מיני מיקרים פרטיים כמו, אם הר"א הוא 1 אז הר"ג הוא 1 (תמיד: ר"א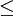 ר"ג
ר"ג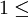 ).
).
עדי
מה בדיוק השיטה למציאת מטריצה מלכסנת P, ולמציאת מטריצה אלכסונית?
מה בדיוק השיטה למציאת מטריצה מלכסנת P, ולמציאת מטריצה אלכסונית?
אם אפשר הסבר..
תודה
D היא המטריצה האלכסונית שהע"ע באלכסונה, P היא המטריצה אשר הו"ע בעמודותיה (מונחים בסדר תואם לערכיהם העצמיים ב-D), והן מקיימות: 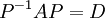 . עדי
. עדי
תמיד אפשר למצוא מטריצה הפוכה למטריצה A ע"י קיילי-המילטון?
אם בפולינום האופייני של A מקבלים אין מחובר שהוא מספר ממשי...איך אפשר יהיה למצוא מטריצה הפוכה ל-A?
אתה מתכוון לאיבר חופשי? אם כן זה אומר שהדט' היא 0 והמט' איננה הפיכה. עדי
בקשר לפתרון של שאלה 5 בתרגיל 6.
http://www.math-wiki.com/images/6/66/89113sol6.pdf
בשורה 4 של הפתרון כתוב:
A^(-2)=(A^(-1))^2
השאלה שלי היא האם זה באמת 1-...או שזה בסך הכל סימון למטריצה הופכית.
כשאומרים ש-A^-1 מטריצה הופכית של A, הכוונה באמת ל-A בחזקת מינוס 1? או שזה רק סימון? אם זה רק סימון, אז למה המעבר שכתוב בשורה 4 נכון?
אני לא בטוחה שהבנתי את השאלה. מז"א "באמת בחזקת מינוס 1?"
באופן כללי במבנים אלגברים "בחזקת מינוס 1" הוא סימון עבור האיבר הופכי (כלומר זה שמעביר לאיבר הנייטרלי. לדוגמא, במספרים 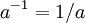 מכיוון ש-
מכיוון ש- 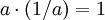 ולכן
ולכן 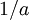 הוא בתפקיד
הוא בתפקיד 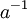 , כי 1 הוא הנייטרלי לכפל מספרים, אבל זה רק מקרה פרטי).
, כי 1 הוא הנייטרלי לכפל מספרים, אבל זה רק מקרה פרטי).
נאמר ש B היא 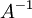 אם AB=BA=I (כי I הוא הנייטרלי לכפל מטריצות), ונקרא ל-B ההופכית ל-A.
אם AB=BA=I (כי I הוא הנייטרלי לכפל מטריצות), ונקרא ל-B ההופכית ל-A.
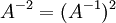 לפי הגדרה, כלומר זה סימון עבור הופכי בריבוע, וזה הסימון בכל מבנה אלגברי. מה שניתן להסיק הוא ש-
לפי הגדרה, כלומר זה סימון עבור הופכי בריבוע, וזה הסימון בכל מבנה אלגברי. מה שניתן להסיק הוא ש-
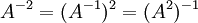 (כלומר שאיבר זה הוא ההופכי ל
(כלומר שאיבר זה הוא ההופכי ל 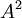 ) וזה בגלל ש-
) וזה בגלל ש-
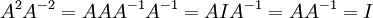 .
.
אם לא הבנתי נכון את השאלה תשלח שוב. עדי
תרגיל 6 שאלה 6
יש לי 3 שאלות:
1.למה מכך ש-rankA=1 ו n>=2 נובע שהמטריצה לא הפיכה ושיש לה ע"ע 0?
נובע שהמטריצה לא הפיכה: מכיוון שדרגת המטריצה מייצגת את מס' השורות הבת"ל במטריצה, וזה מייצג את הפיכותה.
ושיש לה ע"ע 0: היות ולמטריצה לא הפיכה ע"ע 0, 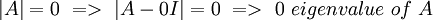 .
.
2.למה מכך ש-rankA=1 נובע ש dim(Av=0)=n-1?
בגלל משפט המימדים.
3.למה הר"ג של ע"ע 0 הוא בין n-1 לבין n?
מכיוון שהריבוי הגיאומטרי הוא n-1, והריבוי האלגברי הוא תמיד גדול או שווה לו.
אשמח לתשובות
תודה!
בכיף. עדי
כמה שאלות
1. שאלה לגבי תרגיל 6 שאלה 1 סעיף ג'
המטריצות הן סכום של בלוקי ז'ורדן?
למה זה עוזר לפתור את השאלה?
מכיוון שב- J-I, כאשר J בצורת ג'ורדן, קל לראות את הדרגה (כי המט' כבר מדורגת).
ועוד שתיי שאלות בקשר לתרגיל 7 שאלה 2:
2. למה להגיד שהפולינום האופייני הוא:
t^3+at^2+tb+c- *
זה כמו להגיד שהפולינום האופייני הוא:
t^3-at^2-tb+c? **
מכיוון שהשורשים יהיו זהים
3. אם זה אותו דבר, אז כשאני מראה שהפולינום המינימלי הוא כמו הביטוי ב-* זה תקין? הרי החזקה הגבוהה של הפולינום המינימלי אמורה להיות עם מקדם 1, ולא 1-, לא?
נכון, תשתמש בצורה **, כלומר 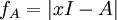 .
.
4.מה האפשרויות עבור הפולינום המינימלי?
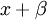 -כלומר פולינום מתוקן מדרגה 1
-כלומר פולינום מתוקן מדרגה 1
או
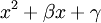 -כלומר פולינום מתוקן מדרגה 2
-כלומר פולינום מתוקן מדרגה 2
או הפולינום האופייני--כלומר פולינום מתוקן מדרגה 3 שבוודאי מאפס את A.
נרצה שהפ"מ יאפס את A. נציב בשני המיקרים הראשונים את  ו-
ו-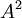 ונראה שלא קיימים
ונראה שלא קיימים 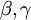 המאפסים את המשוואה. לכן נותר רק הפ"א. עדי
המאפסים את המשוואה. לכן נותר רק הפ"א. עדי
שאלה בקשר העמוד הראשון בתרגול מספר 7
בתחתית העמוד יש 2 דוגמאות.
דוגמה ראשונה עם מטריצת האפס.
דוגמה שנייה עם מטריצת היחידה.
רשום שהפולינום המינימלי של מטריצת היחידה הוא
אחד פחות למדה. איך זה יכול להיות פולינום מינימלי? המקדם של הלמדה הוא 1-
פולינום מינימלי הוא פולינום מתוקן.
זו טעות? אם זו לא טעות, אפשר לקבל הסבר?
הכוונה ללמדה מינוס 1.
שאלה בקשר למציאת בסיס לkerT בהינתן מטריצה מייצגת של T
אני מנסה לפתור את השאלה הבאה:
נתונה ה"ל T:R^4-->R^3 כך שהמטריצה המייצגת שלה ביחס לבסיסים B1 (בסיס של התחום), B (בסיס של הטווח) היא
4 3 2 1
2 0 4 1 = A
10 9 2 2
קבלתי שמרחב הפתרונות של המערכת ההומוגנית המתאימה למטריצה הזו הוא zz span{(-6,1,0,1),(0,-3,2,0)} zz
1. מרחב הפתרונות של המערכת ההומוגנית המתאימה למטריצה A (שהיא כאמור מטריצת ייצוג של T) שווה ל-kerT? אם לא, מה זה בעצם המרחב פתרונות הזה? מה הוא מייצג?
2. במידה והמרחב פתרונות שקבלתי לא שווה ל-kerT מה אני צריך לעשות כעת, על מנת למצוא בסיס/מימד של kerT?
תודה!
ראשית, לא רשמת מה מבקשים בשאלה. שנית אני לא בטוחה איך הגעת לוקטרים האלו (לא בדקתי את הדירוג), אבל אם הם פורשים את הוקטורים v כך ש Av=0 הם אכן וקטורי הקואורדינטות של וקטורי kerT לפי הבסיס 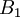 .
.
להזכירך ![[T]^{B_1}_B[v]_{B_1}=[T(v)]_B](/images/math/6/8/f/68f75048837fd3a4e52574c2707e716c.png) , כלומר, לאחר שמצאת בסיס למערכת ההומוגנית של A, עלייך לזכור שזה בסיס של וקטורי קואורדינטות, ושע"מ לתרגם את התוצאה עבור T עלייך לתרגם את וקטורי הקואורדינטות לוקטורים האמתיים, במקרה זה לפי הבסיס
, כלומר, לאחר שמצאת בסיס למערכת ההומוגנית של A, עלייך לזכור שזה בסיס של וקטורי קואורדינטות, ושע"מ לתרגם את התוצאה עבור T עלייך לתרגם את וקטורי הקואורדינטות לוקטורים האמתיים, במקרה זה לפי הבסיס 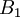 , היות ווקטורי גרעין מגיעים מהתחום.ז"א, כדי למצוא בסיס לkerT עלייך לעבור מוקטורי הקואורדינטות שמצאת לוקטורים ב
, היות ווקטורי גרעין מגיעים מהתחום.ז"א, כדי למצוא בסיס לkerT עלייך לעבור מוקטורי הקואורדינטות שמצאת לוקטורים ב 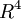 לפי בסיסו במטריצה A.עדי
לפי בסיסו במטריצה A.עדי
מה זה היטל אורתוגונלי? האם צריך להכיר את המושג הזה?
?
לא
תרגיל 9 שאלה 2 סעיף ב'
http://www.math-wiki.com/images/f/f0/89113solution9.pdf
בשורה הרביעית, מהנקודה שבה מתחילה ההוכחה, יש שם מעבר שבהסבר שלו רשום: לינאריות במשתנה הראשון וכמעט לינאריות בשני (המקדמים במשתנים של המשתנה השני הופכים לצמוד שלהם)
לא מובן לי למה מדובר כאן בלינאריות במשתנה הראשון...אולי בגלל שזה סכום עם שלוש נקודות, אז יכול להיות שזה מבלבל אותי.
ומה שעוד לא הבנתי, זה למה המקדמים במשתנים של המשתנה השני הופכים לצמוד שלהם?
לינאריות במשתנה הראשון אומרת
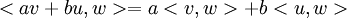
ובאופן כללי
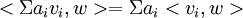 .
.
כזכור 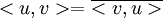 , לכן אם הצירוף הלינארי מופיע ברכיב השני נקבל:
, לכן אם הצירוף הלינארי מופיע ברכיב השני נקבל:
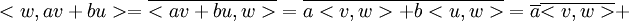
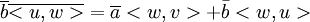
ובאופן כללי
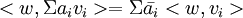 . עדי
. עדי
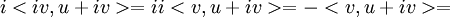
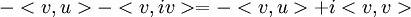
המעבר משמאל לימין נכון? אם כן, למה?
כן, כי i הוא סקלר ולכן ניתן להוציא החוצה. הוספתי את המשך הפיתוח. (להזכירך 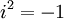 ).
).
ועוד שאלה
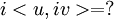
איך אפשר לפתח את זה?
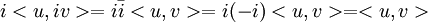 . עדי
. עדי
שאלה
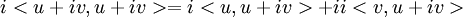
אפשר בבקשה הסבר למעבר הזה???
זה לפי לינאריות ברכיב הראשון:
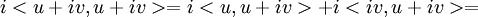
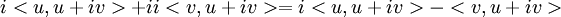 . עדי
. עדי
בהינתן פולינום ב- ![R_3[x]](/images/math/5/8/d/58da1077eba530f10b9265c131818304.png)
איך אני מחשב את הנורמה שלו?
אם יש לי מטריצה...למשל מטריצה מסדר 3x3, איך אני מחשב את הנורמה שלה??
זה תלוי כיצד מוגדרת המ"פ בשאלה. 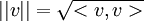
תרגיל 10 שאלה 7
בפתרון של תרגיל 10, שאלה 7, רשום בהתחלה ש"לפי משפט בכיתה, כאשר מוצאים בסיס אורתונורמלי...."
אפשר בבקשה לקבל את הניסוח המלא והמדוייק של המשפט הזה????
לכל קב' בת"ל 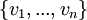 במ"ו V קיימת קב' אורתוגונלית
במ"ו V קיימת קב' אורתוגונלית 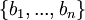 כך שלכל
כך שלכל 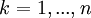 מתקיים
מתקיים
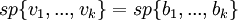 . עדי
. עדי
ובקשר לפתרון שם...הרעיון הוא למצוא בסיס אורתונורמלי בדיוק כמו בשאר השאלות, והדרישות בשאלה
לשיוויונים: {'sp{v1}=sp{v1
sp{v1,v2}=sp{v2',v2'}
נובעות פשוט לפי אותו משפט מהכיתה? כלומר הפתרון עצמו זהה לשאר השאלות מהסוג של מציאת בסיס אוןרתונורמלי לפי התהליך של גרםשמיט , והדרישות שבשאלה נובעות רק מהמשפט? כן
מציאת פ"מ
משום מה אני רואה בתשובות שכדי להוכיח שפ"א = פ"מ אז מציבים את המטריצה בחלק מהפ"מ שרוצים להוכיח ומראים בת"ל. למשל :
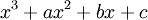 אז מציבים את A^1 ואת A^2 ואומרים שהמטריצות הן בת"ל ולכן הפ"א = לפ"מ .
אז מציבים את A^1 ואת A^2 ואומרים שהמטריצות הן בת"ל ולכן הפ"א = לפ"מ .
אני לא מבינה איך מסיקים את זה
אודה לתשובתך !!:)
שימו לב שכאשר מציבים מטריצה בפולינום מקבלים צירוף לינארי של חזקותיה.
אם הפ"א הוא מדרגה 3, ורוצים שהפ"מ יהיה שווה לפ"א, זה אומר שיש לשלול שהפ"מ הוא מדרגה נמוכה מ-3. כלומר שאם נציב את המט' בפולינום מדרגה 2 או פחות הוא לא יתאפס. הצבת מטריצה בפולינום מדרגה 2 או פחות הוא צ"ל של חזקות המטריצה עד מעלה 2, אם חזקות אלו יהיו בת"ל, הצ"ל הנ"ל לא יתאפס ולכן הפולינום בו הצבנו לא יכול להוות הפ"מ.
אם  לכל b,c
לכל b,c
וגם  k> לכל a,b,c
k> לכל a,b,c
אז 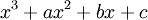 הוא הפולינום המינימלי שמאפס את A.
הוא הפולינום המינימלי שמאפס את A.
עדי