Mathwiki:ארגז חול
מתוך Math-Wiki
שאלה
אני יודעת שאתמול הוכחת לנו את זה לפני השיעור חזרה, אבל זה היה ממש לא מסודר ולא ממש הצלחתי לעקוב, אז אני אשמח אם אתה (או מישהו אחר בכיף(:) יתן תשובה:
ככה: T נורמלי הוכח ש- 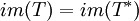
הוכחה
דבר ראשון נוכיח ש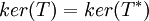 . נניח
. נניח 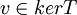 לכן
לכן 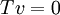 ולכן
ולכן 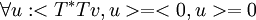 אבל
אבל 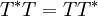 ולכן
ולכן 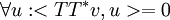 ולכן
ולכן 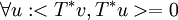 ובפרט זה נכון עבור v=u ולכן
ובפרט זה נכון עבור v=u ולכן 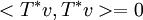 ולכן
ולכן 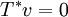 כלומר
כלומר 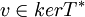 . בכיוון ההפוך ההוכחה דומה.
. בכיוון ההפוך ההוכחה דומה.
עכשיו נוכיח את הטענה. 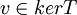 אם"ם
אם"ם 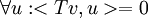 אם"ם
אם"ם 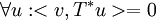 אם"ם
אם"ם 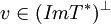 ולכן
ולכן 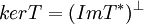 . בצורה דומה
. בצורה דומה 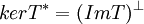 . אבל הגרעינים שווים ולכן
. אבל הגרעינים שווים ולכן 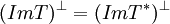 ומזה נובע שהם שווים (כי המרחב המאונך הינו יחיד, והמאונך של המאונך הינו המרחב עצמו).
ומזה נובע שהם שווים (כי המרחב המאונך הינו יחיד, והמאונך של המאונך הינו המרחב עצמו).
