שיחה:88-112 לינארית 1 תיכוניסטים קיץ תשעג
תוכן עניינים
- 1 הוספת שאלה חדשה
- 2 שאלות
- 2.1 שאלה מתרגיל הבית (תרגיל 1)
- 2.2 תשובות לשאלות
- 2.3 תרגיל 1
- 2.4 שאלה מס' 7
- 2.5 דוגמא לתרגיל 9
- 2.6 שאלה 4
- 2.7 שאלה 8ד'
- 2.8 mod 2
- 2.9 שאלות תרגיל 1
- 2.10 שאלה מתרגיל הבית (תרגיל 1)
- 2.11 תרגיל 5
- 2.12 שאלה 2
- 2.13 שאלה 4
- 2.14 תרגיל 1 שאלה 2
- 2.15 הרצאות כתובות
- 2.16 span
- 2.17 כמה הגדרות ואי-הבנות
- 2.18 מימד של Rn[x]
- 2.19 תרגיל 4, שאלות 1,2
- 2.20 תרגיל 4 שאלות 3 ו6
- 2.21 שאלה 8
- 2.22 שאלה על מרחבים וקטוריים....
- 2.23 תרגיל 5 שאלה 11 (דחוף!)
- 2.24 פעולות שורה/עמודה על דטרמיננטות
- 2.25 אי הבנה ברשימת המשפטים למבחן
- 2.26 שיעור חזרה
הוספת שאלה חדשה
הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).
-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן
אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.
שאלות
שאלה מתרגיל הבית (תרגיל 1)
בתרגיל הבית ישנה מטלה: בנו שדה בן 4 איברים. ציינו מהם האיברים הניטרליים לחיבור וכפל.
לא הבנתי כיצד לענות על השאלה ואני לא יודע אפילו מהיכן להתחיל.
- שדה הינו אוסף של איברים, עם פעולות חיבור וכפל בינהם כך שמתקיימים תוכנות מסוימות (חילוף, פילוג, קיבוציות, וכדומה). את רשימת התכונות ניתן למצוא בהגדרה של שדה.
- ידוע לפי התכונות שבשדה יש איבר נייטלי לחיבור ואיבר נייטרלי לכפל, נקרא להם אחד ואפס. לשני האיברים הנותרים נקרא a,b.
- כך, עליך להגדיר פעולות כפל וחיבור בין האיברים, וחשוב לזכור שהתוצאה חייבת להיות בשדה. למשל ניתן להגדיר כי
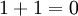 , ואולי
, ואולי  .
. - ניתן לרשום את פעולות הכפל והחיבור בטבלאות כמו שראינו בהרצאה.
- דבר אחרון, יש להוכיח כי הפעולות שהגדרת אכן תואמות את כל התכונות של השדה. --ארז שיינר 19:41, 9 ביולי 2013 (IDT)
תשובות לשאלות
יש אפשרות לתת תשובות סופיות או אופציה לתשובה אפשרית לשאלות? כדי שנוכל לדעת אם צדקנו.. תודה:)
- ארז אמר שכל שבוע יעלו פתרונות של תרגיל הבית מהשבוע הקודם. (אני לא מרצה/מתרגל אז נא לקחת את התשובה שלי בערבון מוגבל)
תרגיל 1
איך אפשר להראות קיבוץ ופילוג כדי להוכיח שקבוצה היא שדה? צריך להראות את זה על כל האיברים? או שאפשר פשוט להגיד שאני משתמש בכפל וחיבור רגילים רק עם מודולו וזה מספיק? תודה מראש
- תלוי. אם אלה המספרים הרגילים עם הפעולות הרגילות אין צורך להוכיח בשנית. אם אתה ממציא איברים חדשים ופעולות עליהם (כמו a,b) אז כן צריך להראות לכל האיברים. --ארז שיינר 11:47, 10 ביולי 2013 (IDT)
שאלה מס' 7
יצא לי בשאלה 7א מטריצה עם המון 13, השורה הראשונה נראתה (26 13 13- 13), זה נכון או שלא הבנתי את פעולת הכפל? ב-7ב יצא לי שזו מטריצה זהה לזו המקורית, זה נכון?
תודה למי שעונה...:)
- יצא לי כמוך ב-7ב אבל ב-7א יצא לי מטריצת האפס..
- גם לי יצא מטריצת האפס ב-א' וב-ב' יצאה לי המטריצה המקורית
- *אני שאלתי את השאלה* תראו, כתבתי תוכנית שמכפילה מטריצות ויצא לי
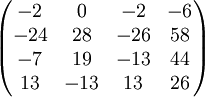
- אז בחישובים אין לי טעות, השאלה היא אם לא הבנתי את הפעולה עצמה.
- לרשותך תוכנה שכופלת מטריצות: כלי עזר לכפל מטריצות- bluebit
- כפל מטריצות מתבצע בצורה הבאה: כדי לגלות את האיבר בשורה ה- i ובעמודה ה- j של AB אנחנו נעבור על השורה ה- i של A ועל העמודה ה- j של B, נכפול איבר-איבר (איבר ראשון בשורה ה- i של A כפול איבר ראשון בעמודה ה- j של B, אח"כ אותו דבר על האיבר השני בשורה i של A ועמודה j של B וכך הלאה...) אחרי זה נסכום את כל מה שיצא, וזה יהיה האיבר במקום ה-i,j ב-A*B. - אופק גילון
- עכשיו הבנתי את הכפל, תודה רבה :)
דוגמא לתרגיל 9
אפשר דוגמא להוכחה בתרגיל 9, כי לא בדיוק תרגלנו את זה או עברנו על דבר כזה בהרצאה. אם מישהו מוכן לכתוב איך מוכיחים ש"מטריצה משולשית עליונה" סגורה לכפל (או לא), הוא יעזור מאוד. תודה.
- דבר ראשון, אתה צודק שעוד לא ראינו כל כך דוגמאות לזה. ביום ראשון תראו בעזרת ה' יותר דוגמאות להוכחות כאלה.
עכשיו בקשר לשאלה עצמה - לפי ההגדרה מטריצה משולשית עליונה היא מטריצה שבה 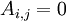 כאשר
כאשר 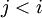 .
.
כלומר (אם אתה מחליט שאתה רוצה להוכיח ולא להפריך) אתה רוצה להוכיח שאם 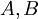 מקיימות את התנאי הזה אז גם
מקיימות את התנאי הזה אז גם 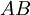 מקיימת אותו
מקיימת אותו
עכשיו, לפי הגדרת כפל אתה יודע למה שווה 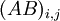 . אתה צריך להראות שאם
. אתה צריך להראות שאם 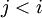 אז זה שווה ל
אז זה שווה ל 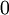 .
.
--איתמר שטיין 09:35, 11 ביולי 2013 (IDT)
- זה ברור, השאלה היא איך ההוכחה מתבצעת - באיזו דרך. באופן כללי הצלחתי להפוך את הטענה לטענה הבאה: בכל עבור כל שורה
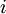 ועמודה
ועמודה 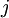 , מובטח שכאשר
, מובטח שכאשר 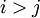 יהיו אפסים באופן הבא: עד ההגעה ל"אלכסון הראשי" במטריצה הראשונה, האפסים במכפלה ילקחו ממנה, ומן ההגעה האפסים ילקחו מהמטריצה השנייה (מקווה שהבהרתי את עצמי). אבל איך אני מוכיח שבכל המכפלות יש
יהיו אפסים באופן הבא: עד ההגעה ל"אלכסון הראשי" במטריצה הראשונה, האפסים במכפלה ילקחו ממנה, ומן ההגעה האפסים ילקחו מהמטריצה השנייה (מקווה שהבהרתי את עצמי). אבל איך אני מוכיח שבכל המכפלות יש 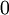 ?
?
- אני לא בטוח שהבנתי את המשפט "להוכיח שבכל המכפלות יש
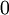 ." (באיזה מכפלות?). לפי מה שאתה כותב כאן, יש לך כמעט את התשובה ביד.--איתמר שטיין 19:01, 11 ביולי 2013 (IDT)
." (באיזה מכפלות?). לפי מה שאתה כותב כאן, יש לך כמעט את התשובה ביד.--איתמר שטיין 19:01, 11 ביולי 2013 (IDT)
- הכוונה היא שאחד מהגורמים במכפלה הוא
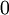 בכל אחת מהמכפלות
בכל אחת מהמכפלות 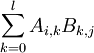 ולכן גם הסכום הוא
ולכן גם הסכום הוא 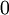 , ומכאן שערך כל אחד מהתאים עבור
, ומכאן שערך כל אחד מהתאים עבור 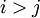 הוא גם
הוא גם 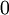 ולכן הטענה נכונה.
ולכן הטענה נכונה.
- אתה הרי יודע ש
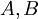 הם מטריצות משולשיות עליונות ולכן אתה יודע שהרבה מהאיברים שלהם הם
הם מטריצות משולשיות עליונות ולכן אתה יודע שהרבה מהאיברים שלהם הם 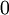 .
.
אתה רק צריך להסביר למה לכל 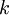 שהוא בין
שהוא בין 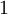 ל
ל 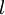 אחד מהגורמים במכפלה שכתבת
אחד מהגורמים במכפלה שכתבת  או
או 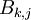 (או שניהם כמובן) יהיה
(או שניהם כמובן) יהיה 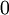 . יש לך ממש את התשובה, זה רק עוד טיעון קטן.
. יש לך ממש את התשובה, זה רק עוד טיעון קטן.
--איתמר שטיין 12:47, 12 ביולי 2013 (IDT)
שאלה 4
בוקר טוב !
בשאלה ארבע ישנה מערכת משוואות עם פרמטר b. האם ידוע לנו אודות הפרמטר? האם הוא שונה מאפס? או שהאם הוא יכול להיות גם שווה?
תודה ושבת שלום!
- לא ידוע כלום. יכול להיות שווה ויכול להיות שונה (כמובן שאתה יכול לחלק את התשובה שלך לפי המצבים השונים).--איתמר שטיין 12:48, 12 ביולי 2013 (IDT)
שאלה 8ד'
בשאלה 8ד' שכתוב 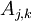 האם הכוונה היא ל-
האם הכוונה היא ל-![[A]_{j,k}](/images/math/5/c/d/5cd61ae61da28cb37f082f940acba44d.png) (סקלר)?
--Omer rosler 12:02, 12 ביולי 2013 (IDT)
(סקלר)?
--Omer rosler 12:02, 12 ביולי 2013 (IDT)
- כן, זה סקלר. האיבר ה
 של
של  .--איתמר שטיין 12:49, 12 ביולי 2013 (IDT)
.--איתמר שטיין 12:49, 12 ביולי 2013 (IDT)
mod 2
אפשר בmod 2 את הדבר הבא? שבגלל ש-1=1 cis 240=cis60 *cis 180=-1*cis 60=1*cis 60=cis60
- מה זה מוד 2? אנו מכירים את השדה
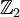 שמכיל את האיברים 0 ו-1 בלבד. אין קשר בינו לבין מספרים מרוכבים. --ארז שיינר 19:48, 12 ביולי 2013 (IDT)
שמכיל את האיברים 0 ו-1 בלבד. אין קשר בינו לבין מספרים מרוכבים. --ארז שיינר 19:48, 12 ביולי 2013 (IDT)
שאלות תרגיל 1
בשאלה 7 בסעיף ב׳ קיבלתי שעבור חזקות אי זוגיות המטריצה שמתקבלת שווה למטריצה בהתחלה. האם צריך להוכיח את התכונה? או שמספיק לרשום אותה במילים? בשאלה 8 בסעיפים ב׳ ו-ד׳ כתוב Ek,l האם זוהי מטריצה אחרת ואם כן מה ידוע עליה?
- לגבי שאלה 7, פשוט תכתוב שהמטריצה בחזקת 2013 שווה למטריצה אחרת בחזקת 2012 ואז למקורית בחזקת 2011, ואז לרשום שבגלל שהמטריצה חזרה להיות מקורית יש מחזוריות - בכל 2 הכפלות המטריצה חוזרת לעצמה. לגבי שאלה 8, ידוע שלמטריצה
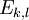 יש 1 במיקום ה-
יש 1 במיקום ה-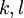 ובכל שאר המקומות אפסים. - יאיר (אני לא מרצה / מתרגל אז נא לקחת את התשובה בעירבון מוגבל).
ובכל שאר המקומות אפסים. - יאיר (אני לא מרצה / מתרגל אז נא לקחת את התשובה בעירבון מוגבל).
בשאלה 7 אתה לא חייב להוכיח את התכונה, כל דרך שבה תסביר למה שווה המטריצה בחזקת 2013 זה בסדר.--איתמר שטיין 10:05, 14 ביולי 2013 (IDT)
שאלה מתרגיל הבית (תרגיל 1)
בתרגיל הבית ישנה תרגיל 4:אני לא יודע כלום על משתנים a b ולא הבנתי כיצד לענות על השאלה ואני לא יודע אפילו מהיכן להתחיל. אשמח לקבל אולי דוגמא לפתרון תרגיל דומה שמכיל משתנים וגם מסדר MOD או הסבר שיעזור לי לפתור את זה
- a,b הם פרמטרים. בעצם אתה צריך לפתור 3 משוואות ב-3 נעלמים כאשר a,b פרמטרים, ממש כמו בתיכון. ההבדל היחיד פה הוא שאתה ב-
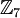 ולכן עליך לדאוג לכך שאתה משתמש רק באיברי השדה. ככה אם תקבל מצב של a+6+4 (סתם דוגמה), אתה צריך להמיר את זה ל- a+3 ולא a+10. הנה קישור לאלגוריתם לדירוג מטריצה שיכול לעזור : אלגוריתם לדירוג מטריצות, מקווה שזה עוזר.- אופק
ולכן עליך לדאוג לכך שאתה משתמש רק באיברי השדה. ככה אם תקבל מצב של a+6+4 (סתם דוגמה), אתה צריך להמיר את זה ל- a+3 ולא a+10. הנה קישור לאלגוריתם לדירוג מטריצה שיכול לעזור : אלגוריתם לדירוג מטריצות, מקווה שזה עוזר.- אופק
תרגיל 5
איך אני אמור למצוא מערכת משוואות עבור 121 פתרונות בתרגיל כזה או למשל עבור N פתרונות אחרים? אם אפשר אני זקוק לדוגמה או הסבר.
- משפט: למערכת משוואות מעל שדה עם מאפיין
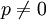 ועם n משתנים חופשיים, יהיו
ועם n משתנים חופשיים, יהיו 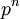 פתרונות.(ההיגיון הוא שלכל משתנה חופשי יש לי p אפשרויות להציב בו) --Ofekgillon10 21:03, 13 ביולי 2013 (IDT)
פתרונות.(ההיגיון הוא שלכל משתנה חופשי יש לי p אפשרויות להציב בו) --Ofekgillon10 21:03, 13 ביולי 2013 (IDT)
שאלה 2
בשאלה 2, האם מספיק למצוא את טבלאות החיבור והכפל של השדה, או שחייבים להוכיח שכל התכונות מתקיימות. אם כן, יש דרך לעשות את זה מלבד לעבור על כל האיברים ולהראות?
- צריך גם להוכיח שזה שדה. את הקיום של רוב התכונות קל לראות מהטבלאות. גם את התכונות שלא קל לראות מהטבלאות לא בהכרח צריך לעבור על כל המקרים הקיימים - כי יכול להיות שקל מאוד להסביר את חלקם. אבל כן, עבור חלק מהתכונות צריך לעבור על חלק מהאפשרויות.--איתמר שטיין 10:08, 14 ביולי 2013 (IDT)
שאלה 4
אם לאחר דירוג המטריציה יצא לי שורת אפסים אחת כאשר אני נמצא מעל Z7 אז יש לי 7 פתרונות אפשריים? והאם אני רושם את התשובה באופן הבא: פתרון אחד... אין פתרון... 7 פתרונות... ?
- כן. אם מעל
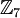 יש משתנה אחד חופשי אז יש
יש משתנה אחד חופשי אז יש 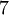 פתרונות.--איתמר שטיין 17:45, 18 ביולי 2013 (IDT)
פתרונות.--איתמר שטיין 17:45, 18 ביולי 2013 (IDT)
- אז בעצם בתשובה אני רושם : אם a=2,5 וגם b=0 יש 7 פתרונות ולא אינסוף פתרונות?
- מספר הפתרונות שווה למספר האיברים בשדה בחזקת מספר המשתנים החופשיים. מעל שדה סופי לא ייתכנו איסוף פתרונות, ולכן אסור לרשום זאת. --ארז שיינר
תרגיל 1 שאלה 2
למדנו בהרצאה (למרות שלא כתבנו) משפט שאומר כי לכל p ראשוני קיים שדה אחד ויחיד בעל 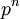 איברים.
אם מניחים כי קיים שדה בעל 4 איברים, אפשר להראות כי הכפל והחיבור שלו יכולים להיות מוגדרים בדרך אחת בלבד, לכן זה חייב להיות השדה ללא הוכחת כל התכונות של שדה. כי אם הקבוצה {0,1,a,b} עם הפעולות שהגדרנו לא שדה אז זו סתירה למשפט (הפעולות לא יכולות להיות מוגדרות אחרת כי זו סתירה לתכונות של שדה).
האם זו הוכחה מספקת לשאלה 2?--Omer rosler 23:33, 19 ביולי 2013 (IDT)
איברים.
אם מניחים כי קיים שדה בעל 4 איברים, אפשר להראות כי הכפל והחיבור שלו יכולים להיות מוגדרים בדרך אחת בלבד, לכן זה חייב להיות השדה ללא הוכחת כל התכונות של שדה. כי אם הקבוצה {0,1,a,b} עם הפעולות שהגדרנו לא שדה אז זו סתירה למשפט (הפעולות לא יכולות להיות מוגדרות אחרת כי זו סתירה לתכונות של שדה).
האם זו הוכחה מספקת לשאלה 2?--Omer rosler 23:33, 19 ביולי 2013 (IDT)
- אם אתה יודע מראש שקיים שדה בגודל
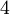 אז זאת הוכחה נכונה. למרות שבעיקרון הכוונה הייתה גם שתוכיחו שזה שדה.
אז זאת הוכחה נכונה. למרות שבעיקרון הכוונה הייתה גם שתוכיחו שזה שדה.
--איתמר שטיין 15:06, 22 ביולי 2013 (IDT)
הרצאות כתובות
איפה אפשר לראות את ההרצאות המוקלדות? לא התרגולים... כלומר את כל מה שנרשם בהרצאה (בעיקר הוכחות למשפטים שהיו בהרצאה)
אני לא חושב שיש את ההרצאות מוקלדות איפשהוא. הוכחות למשפטים אפשר למצוא בספרים. כולל אלה שיש להם קישורים באתר.--איתמר שטיין 16:17, 29 ביולי 2013 (IDT)
span
איך אני מוצא כי (B מוכל ב - V)
SPAN(B) = V
אם נתון לי B?
- תשובה: אם אני מבין את השאלה שלך. אתה שואל, בהינתן קבוצה
 איך אני מראה ש
איך אני מראה ש 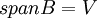 .
.
יש 2 דרכים די סטנדרטיות:
דרך 1: להראות שבעזרת צירופים לינאריים של איברי  אפשר להגיע לקבוצה שפורשת את
אפשר להגיע לקבוצה שפורשת את  .
.
דרך 2: להראות ש  מכילה קבוצה בת"ל בגודל המימד של
מכילה קבוצה בת"ל בגודל המימד של  (ואז לפי השלישי חינם היא גם פורשת).
(ואז לפי השלישי חינם היא גם פורשת).
מקווה שההסבר הזה ברור.--איתמר שטיין 10:09, 30 ביולי 2013 (IDT)
כמה הגדרות ואי-הבנות
החסרתי כמה שיעורים, ולא הצלחתי להשלים את כל החומר. אשמח לתשובה קצרה על כמה שאלות:
- המושגים -
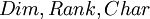 , מה כל אחד מהם אומר?
, מה כל אחד מהם אומר? - כשמתכוונים לבסיס סטנדרטי (S) של
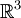 , הכוונה היא לווקטורים
, הכוונה היא לווקטורים 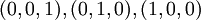 ?
? - מטריצת מעבר בין בסיסים היא בין שני בסיסים שונים שפורשים את אותו מרחב ווקטורי?
תודה מראש...
תשובות:
1) 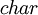 זה מאפיין של שדה. המאפיין של שדה
זה מאפיין של שדה. המאפיין של שדה  הוא מספר הפעמים שצריך לסכום את
הוא מספר הפעמים שצריך לסכום את 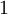 כדי להגיע ל
כדי להגיע ל 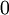 .
.
למשל ב 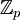 אם תסכום
אם תסכום 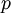 פעמים את
פעמים את 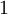 תקבל 0.
תקבל 0.
אם לעולם לא תקבל 0, אז המאפיין הוא 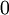 .
.
לכן 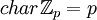 ו
ו 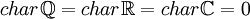
אפשר להוכיח שהמאפיין הוא תמיד 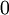 או מספר ראשוני.
או מספר ראשוני.
2)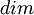 . לכל מרחב וקטורי
. לכל מרחב וקטורי  המימד שלו
המימד שלו 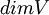 הוא מספר הוקטורים שיש בבסיס.
הוא מספר הוקטורים שיש בבסיס.
(אחד המשפטים שהוכחתם בהרצאה אומר שכל שני בסיסים הם באותו גודל).
3)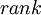 : דרגה של מטריצה היא המימד של מרחב השורות ומסתבר (זה משפט שראיתם/תראו בהרצאה) שזה שווה למימד של מרחב העמודות.
: דרגה של מטריצה היא המימד של מרחב השורות ומסתבר (זה משפט שראיתם/תראו בהרצאה) שזה שווה למימד של מרחב העמודות.
(יש גם מושג של דרגה של העתקה לינארית - שיש לו קשר הדוק לדרגה של מטריצה אבל לזה עוד לא הגענו).
- כן.
- כן.
--איתמר שטיין 14:41, 31 ביולי 2013 (IDT)
מימד של Rn[x]
מה המימד של המ"ו Rn[x]=V? ע"פ הבסיסים הסטנדרטיים, DimV=n+1, האם זה נכון?
אם כן, בשאלה 1ג בתרגיל 3, כיצד ייתכן ש-3 ווקטורים יפרשו את R3[x]=V?
אם לא, ומתקיים DimV=n, אז איך בבסיס, לדוגמא של R3[x]=V יש את 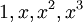 ?
?
- (לא מתרגל / מרצה) אכן,
![\dim\left (\mathbb{R}_n\left [ x \right ] \right )=n+1](/images/math/6/3/0/630c36c45a709f4cdb985ef1b5fb4afb.png) (ניתן להוכיח, למשל, עם הבסיס הסטנדרטי). אם הם אינם יכולים לפרוש את הקבוצה, לפי השאלה, יש למצוא בסיס שיכיל את הקבוצה, כלומר להרחיב את הקבוצה הזו לבסיס. --גיא בלשר 17:03, 31 ביולי 2013 (IDT)
(ניתן להוכיח, למשל, עם הבסיס הסטנדרטי). אם הם אינם יכולים לפרוש את הקבוצה, לפי השאלה, יש למצוא בסיס שיכיל את הקבוצה, כלומר להרחיב את הקבוצה הזו לבסיס. --גיא בלשר 17:03, 31 ביולי 2013 (IDT)
גיא צודק. באמת לא ייתכן ש 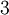 וקטורים יפרשו את
וקטורים יפרשו את ![\mathbb{R}_3[x]](/images/math/8/4/e/84ef8e18caf28275bb31fb78edc3a348.png) . נימוק משיקולי מימד הוא באמת הנימוק הפשוט ביותר.--איתמר שטיין 09:42, 1 באוגוסט 2013 (IDT)
. נימוק משיקולי מימד הוא באמת הנימוק הפשוט ביותר.--איתמר שטיין 09:42, 1 באוגוסט 2013 (IDT)
תרגיל 4, שאלות 1,2
לגבי שאלה 1ב - איך אני מוצא את הבסיס ל-W? ולגבי שאלה 2 - למה מתכוונים בסעיף א'? זה לא ברור, לפחות לי.
- תשובה: לגבי 1: אתה יכול לתאר את
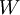 בתור פתרון למערכת משוואות הומוגנית.
בתור פתרון למערכת משוואות הומוגנית.
אחרי שיש לך מערכת משוואות הומוגנית אפשר לפתור אותה, וקל למצוא את הבסיס מהפתרון הכללי. (כמו בתרגיל 3 - שאלה 5).
שאלה 2: צריך למצוא מערכת משוואות לינארית הומוגנית שמרחב הפתרונות שלה הוא בדיוק  .
--איתמר שטיין 10:15, 9 באוגוסט 2013 (IDT)
.
--איתמר שטיין 10:15, 9 באוגוסט 2013 (IDT)
תרגיל 4 שאלות 3 ו6
בס"ד
- בשאלה 3 סעיף ד'-כיצד ניתן למצוא את מטריצת המעבר?
- בשאלה 6-מה אומר לנו המשפט C(B) n N(A)=0 ?
(n זה החיתוך...) לא הבנתי את המשפט...
תודה מראש :)
- (לא מרצה / מתרגל).
- לגבי 3-ד', בתרגול קיבלנו אלגוריתם למציאת מטריצת מעבר בין בסיסים. מצא את
![[I]_{C}^{S}](/images/math/d/7/0/d70dcb800a55a883bcde99fbb5957ae7.png) ואת
ואת ![[I]_{B}^{S}](/images/math/c/7/5/c75e4d7bf82fb7f166452b06a175fdce.png) . כעת הפוך את
. כעת הפוך את ![[I]_{C}^{S}](/images/math/d/7/0/d70dcb800a55a883bcde99fbb5957ae7.png) (כלומר מצא את ההופכית) וקיבלת את
(כלומר מצא את ההופכית) וקיבלת את ![[I]_{S}^{C}](/images/math/d/1/3/d13a921ae4f1c1712a17cfdb8ea11af4.png) ע"פ המשפט שלמדנו בשיעור. כעת מתקבל
ע"פ המשפט שלמדנו בשיעור. כעת מתקבל ![[I]_{C}^{B}=[I]_{C}^{S}*[I]_{S}^{B}](/images/math/e/c/2/ec2430613c34a80ca21cd926bb03d816.png) וקיבלת את מטריצת המעבר מ-B ל-C.
וקיבלת את מטריצת המעבר מ-B ל-C. - לגבי 6 - כל הקטע בשאלה הוא להבין מה אומר המשפט. אני אתן רמז כי חבל לגלות את התשובה, הפתרון יפה. אני אגיד רק שמתקיים
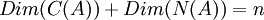 עבור
עבור 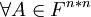 וכן שכל
וכן שכל 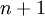 ווקטורים במ"ו
ווקטורים במ"ו 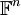 תלויים ליניארית (כמובן שזכור ש-
תלויים ליניארית (כמובן שזכור ש-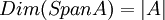 ). זה אמור להספיק, חבל לגלות הכל.
). זה אמור להספיק, חבל לגלות הכל.
- לגבי 3-ד', בתרגול קיבלנו אלגוריתם למציאת מטריצת מעבר בין בסיסים. מצא את
- -- יאיר קורנגוט 23:32, 8 באוגוסט 2013 (IDT)
שאלה 8
בתרגיל בית האחרון (5), לא הבנתי איך תיראה דוגמא להעתקה לינארית בתרגיל השמיני. איך מביעים העתקה ממרחב הפולינומים למרחב הפולינומים ? ( (?)T =? )
- תשובה: דרך טובה לתאר העתקה זה לומר מה היא עושה לוקטורים של הבסיס הסטנדרטי.
נניח 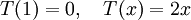 .
.
או לכתוב 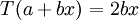
שזה אותו דבר. --איתמר שטיין 22:12, 17 באוגוסט 2013 (IDT)
שאלה על מרחבים וקטוריים....
אם הווקטור היחיד במרחב וקטורי כלשהו הוא ווקטור האפס, אז הבסיס למרחב הוא ווקטור האפס או הקבוצה הריקה?
- תשובה: הקבוצה הריקה.--איתמר שטיין 22:13, 17 באוגוסט 2013 (IDT)
תרגיל 5 שאלה 11 (דחוף!)
בתרגיל 5 שאלה 11 מה זה z עם 3 וp? זה סימון שאני לא חושב שלמדנו...
- אנחנו דיברנו על מרחב וקטורי מהצורה
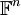 . במקרה הזה השדה הוא
. במקרה הזה השדה הוא 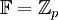 .--איתמר שטיין 22:14, 17 באוגוסט 2013 (IDT)
.--איתמר שטיין 22:14, 17 באוגוסט 2013 (IDT)
פעולות שורה/עמודה על דטרמיננטות
כאשר אני רוצה לחשב דטרמיננטה של מטריצה, אני יכול לעשות פעולות שורה ופעולות עמודה בערבוב (יעני להחליף בין עמודות, או להוסיף עמודה כפול סקלר לעמודה אחרת, ואח"כ להכפיל שורה בסקלר וכו')? כי לא צריך לשמור על סדר המשתנים והכל... נכון?
- כן, זה לא משנה. זה גם קל להסביר למה זה נכון. ביצוע פעולות שורה הוא כמו כפל של מטריצה מימין במטריצות אלמנטריות, ביצוע פעולות עמודה זה כמו כפל משמאל במטריצות אלמנטריות. אם אתה לוקח מטריצה
 ומבצע עליה פעולות שורה ועמודה אז קיבלת
ומבצע עליה פעולות שורה ועמודה אז קיבלת
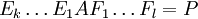 כאשר
כאשר 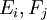 הם מטריצות אלמנטריות ו
הם מטריצות אלמנטריות ו  זאת המטריצה שקיבלת.
זאת המטריצה שקיבלת.
אבל בגלל שדטרמיננטה היא כפלית
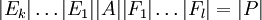
ולכן
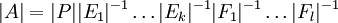 .
--איתמר שטיין 10:44, 19 באוגוסט 2013 (IDT)
.
--איתמר שטיין 10:44, 19 באוגוסט 2013 (IDT)
אי הבנה ברשימת המשפטים למבחן
לא הבנתי מה בעצם המשפט השלישי. הרי זו ההגדרה של מטריצה הפיכה, אם יש מטריצה אחרת שכאשר כופלים אותה משמאל במטריצה שלנו המכפלה שווה I (מטריצה הזהות). אז מה בעצם אנו אמורים להוכיח במשפט הזה?
שיעור חזרה
באיזו יום יקיים שיעור חזרה,ואם כן באיזה שעות זה יתקיים?
- יום שלישי בשעה 15:00. (השעה עוד לא סופית).--איתמר שטיין 20:43, 24 באוגוסט 2013 (IDT)