לינארית 1 לתיכוניסטים תש"ע - שאלות ותשובות

$\dim W+U= \dim W + \dim U - \dim W\cap U$

הוראות

כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחילת הדף את השורה הבאה:

== כותרת לשאלה ==

לכתוב מתחתיה את שאלתכם, וללחוץ על שמירה למטה מימין

הודעה חשובה !!! - יש להגיש את התרגילים הנוספים (13 , ו 14 כרשות למי שמגיש ) עד ,וכולל , 16.9.2010 ! למשל לתא הבודקת הילה הלוי בכר , או לתומר ביום רביעי או לניר ביום חמישי - בתרגולי החזרה . אנא הודיעו למי שאתם יודעים שלא יגיע לתרגולים אלו . תודה:)

ארכיון

ארכיון 1 - תרגיל 1

ארכיון 2 - תרגיל 2

ארכיון 3 - בוחן + תרגיל 3

שאלות

6.30 ב'

רציתי לשאול האם מותר לי כחלק מפעולת הדרוג לכפול בcos או בsin כסקלר, כלומר בפעולה האלמנטרית שאני מכפיל..?

תשובה

רק בנקודות בהן הם לא מתאפסים. אחר כך צריך לבדוק מה קורה בנקודות שהם מתאפסים בנפרד. כמו בדירוג עם פרמטר.

שאלה 1 מקובץ התרגילים

בשאלה 1 ד',כתוב מקיים את מערכת המשוואות שמכילה את המשוואות מסעיף א וגם ב. המשוואות מא' וב' הם אותו משוואות, האם הכוונה לסעיף א וסעיף ג?
תודה

6.30

שלום, רציתי לשאול אם יש עוד דרכים למצוא מטריצה הפיכה חוץ מלדרג את המטריצה ולהפעיל את אותן פעולות אלמנריות על מטריצת היחידה?

תשובה

במטריצות 2 על 2 למדתם על שיטה מקוצרת. מעבר לכך אני לא יכול לחשוב על שיטה פרקטית יותר (מאשר לפתור מערכת עם מליון משוואות ומליון נעלמים :) )

במילים אחרות, אין "נוסחא" פשוטה להפוך מטריצה 3 על 3 (אתה מוזמן לנסות לחשב את הנוסחא הזו בעצמך), ואין דבר פשוט מלדרג מטריצה.

תרגיל 6.23

מותר לי להשתמש בנוסחה של סדרה הנדסית לשם ההוכחה,או שזה בעצם מה שאני אמור להוכיח?

תשובה

זה מה שצריך להוכיח.. הרי זו בדיוק הנוסחא.

עוד שאלה על 6.34

הצלחתי להבין שאם אכפול את המטריצה של המקדמים של מערכת המשוואות במטריצה ההופכית של A, אקבל את מט' הזהות. הבעיה היא 2 העמודות של האיקסים שנותרו- האם אני יכול "לפצל" את המטריצה ל3 העמודות הראשונוות ול2 הנותרות, לכפול רק את המטריצה הראשונה (שפיצלתי) במטריצה ההופכית של A, ואז להחזיר את המטריצות המפוצלות חזרה למטריצה אחת? אם כן, למה מותר לעשות את זה, ואיך עושים את זה? (איך קוראים לפעולה הזאת ומה הנימוק שאפשר לתת לה?) בנוסף, איך המטריצה של התשובות (123) מתנהגת? כלומר, כשאני מפצל את המטריצות, אני צריך לשים את המטריצה של התשובות מימין לכל אחת מהמטריצות שפיצלתי? אני לא מבין איך כל זה מתנהג. תודה!

בקשה מארז שיינר- המתרגל של שיעור התגבור בלינארית (אם אפשר...)

ארז, בפעם הקודמת שיעור התגבור בלינארית הלך ללא הכנה, בלי שהכנת תרגילים שיהיה אפשר לעשות בו ובעצם בלי מה לעשות. אפשר לבקש שלשיעור התגבור הבא תכין כמה תרגילים מאתגרים שיכולים להופיע בבוחן/מבחן, במיוחד שאלות שמצריכות שימוש במכפלה במטריצות בסיסיות (כמו בשאלה שהייתה בשיעורי הבית), הוכחות עם מטריצות, וכו'? אני חושב שיהיה עדיף לעשות תרגילים נוספים, מאשר רק לחזור על הגדרות שאותן פשוט אפשר לקרוא מההרצאות. אם אפשר, ארצה לבקש אותו דבר גם מאדם בתגבור של בדידה. תודה רבה!

תשובה

שיעור התגבור איננו שיעור חזרה לקראת בוחן/מבחן. מטרת השיעור היא לעזור לתלמידים שמתקשים להדביק את קצב הקורס. תרגילים מאתגרים - מהגדרתם - אינם מתאימים לשיעור תגבור.

תרגילים על מטריצות בסיסיות יש מספיק בשיעור ובשיעורי הבית. אם הפתרונות לא מובנים (זה בהנחה שהם נקראו) ניתן לעבור עליהם שוב ולהסביר.

השיטה של פתרון תרגילים מסוגים שונים על מנת ללמוד לבוחן/מבחן עובדת בבגרות אך לא באוניברסיטה. בקורס אקדמי חייבים להבין את ההגדרות ואת המשפטים ואת הרעיונות המרכזיים בחומר. מטרת התגבור היא לעזור בביצוע משימה זו.

ארז.

תרגיל 2.9

בשאלה מראים ש 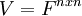$V=F^{nxn}$. מה זה? הרי V זה מ"ו, לא מרחב של מטריצות... ומטריצות זה אוסף של וקטורים, לא וקטור- יש בהם מחלקי אפס אז הם בכלל לא יכולות להיות מ"ו.. בקיצור פשוט תסבירו מה הכוונה של מה שכתבתי קודם..

תשובה

• מרחב המטריצות הוא אכן מרחב וקטורי עם פעולות חיבור מטריצות וכפל בסקלר הידועות.
• מחלקי אפס אין בשדה. במ"ו אין כפל בין וקטורים ולכן אין משמעות למחלקי אפס.
• מטריצות זה לא אוסף של וקטורים. מטריצה זו טבלה של מספרים, והיא וקטור בעצמה (כאשר מסתכלים על המטריצות כמרחב וקטורי)

שאלה על משפט

המשפט: V מ"ו מעל שדה F תהי K שמוכלת בV. אם K מוכלת בU שהוא תת מרחב של V אז SPK מוכל בU.

ההוכחה שהמרצה כתב: ניקח u ששיך לSPK ונאמר שu שווה לסיגמה של אלפא (במקום הi) כפול v (במקום הi.)כאשר v שייך לK. כיוון שv שייך לK ןK מוכל בU הרי v שייך לU, אבל U תת מרחב של V ןלכן סגור לצרופים לינאריים. לכן u ששווה לסיגמה של אלפא (במקום הi) כפול v (במקום הi),שייך לU.

אני לא ממש הבנתי את ההוכחה, אם U סגור לצרופים לינאריים איך זה הגיוני שu שייך U?

תשובה

מה הכוונה איך זה הגיוני? זה מה שסגירות אומרת.

סגירות בU אומרת שלכל וקטורים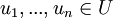$u_1,...,u_n \in U$ ולכל סקלרים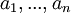$a_1,...,a_n$ מתקיים 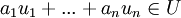$a_1u_1+...+a_nu_n \in U$. (זה נובע מתכונות הסגירות לכפל בסקלר וחיבור של מרחב וקטורי - והרי U הוא מ"ו).

שאלה 6.37

בסע' ג' אסור לי להניח שאם A הפיכה אז היא בעצם מקיימת את מה שנדרש מ-P, נכון?

מה זאת אומרת מה שנדרש מP? כלומר 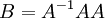$B=A^{-1}AA$? אין סיבה להניח דבר כזה... כי הרי זה שווה A