קשר בין לכסינות לבין הפולינום המינימלי
משפט
 לכסינה
לכסינה  הפולינום המינימלי שלה הוא מהצורה
הפולינום המינימלי שלה הוא מהצורה 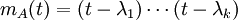 עבור
עבור 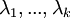 הע"ע השונים של
הע"ע השונים של 
הוכחה
 לכסינה ולכן קיים בסיס של ו"ע של
לכסינה ולכן קיים בסיס של ו"ע של  נקרא לו
נקרא לו 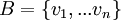 . ברור שהפולינום המינימלי של
. ברור שהפולינום המינימלי של  חייב להכיל את הגורמים האי פריקים
חייב להכיל את הגורמים האי פריקים 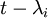 לכל הע"ע של
לכל הע"ע של  . לכן אם הפולינום
. לכן אם הפולינום 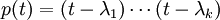 מקיים
מקיים 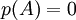 אזי הוא הפולינום המינימלי (בוודאי אין פולינום קטן ממנו...)
אזי הוא הפולינום המינימלי (בוודאי אין פולינום קטן ממנו...)
אנו יודעים שעבור כל 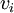 קיים
קיים 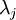 כך ש
כך ש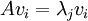 . מה הערך של
. מה הערך של 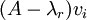 עבור
עבור 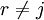 ?
?
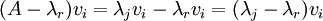
הבה נסתכל ב 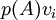 :
:
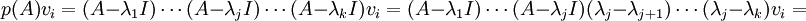
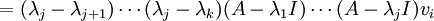
אבל 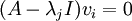
ולכן 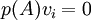 לכל
לכל 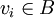
 בסיס ולכן כל וקטור
בסיס ולכן כל וקטור 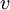 ניתן להצגה כצירוף לינארי של איברי
ניתן להצגה כצירוף לינארי של איברי  :
:
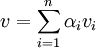
ולכן 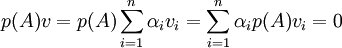
אם 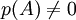 אז קיימת לה עמודה
אז קיימת לה עמודה 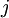 שונה מאפס, אזי
שונה מאפס, אזי 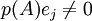 . אבל ראינו ש
. אבל ראינו ש 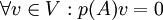 ולכן
ולכן 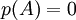 ולכן
ולכן 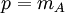 .
.
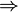
קודם כל הפולינום המינימלי של  מכיל גורמים לינאריים בלבד ולכן כך גם הפולינום המאפיין של
מכיל גורמים לינאריים בלבד ולכן כך גם הפולינום המאפיין של  .
.
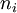 כלומר החזקה של הגורם
כלומר החזקה של הגורם 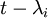 בפולינום המינימלי שווה לאחד עבור כל אחד מהע"ע של
בפולינום המינימלי שווה לאחד עבור כל אחד מהע"ע של  . לכן לפי משפט הקיום והיחידות של ז'ורדן הבלוק המקסימלי של כל ע"ע בצורת הז'ורדן של
. לכן לפי משפט הקיום והיחידות של ז'ורדן הבלוק המקסימלי של כל ע"ע בצורת הז'ורדן של  הוא מגודל אחד. כלומר
הוא מגודל אחד. כלומר  לכסינה (כי היא סכום ישר של מטריצות בגודל
לכסינה (כי היא סכום ישר של מטריצות בגודל 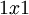 .
.