לינארית 1 לתיכוניסטים תש"ע - שאלות ותשובות
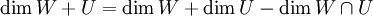
תוכן עניינים
- 1 הוראות
- 2 ארכיון
- 3 שאלות
- 3.1 לכל בסיס של V (מ"ו מסוים) יש אותו מספר איברים
- 3.2 שאלה בדירוג מטריצה לבדיקת תלות לינארית
- 3.3 דרך הפתרון ל7.9
- 3.4 בקשה
- 3.5 שאלה על בסיסים ומ"וים
- 3.6 שאלה
- 3.7 שאלה
- 3.8 7.20
- 3.9 שאלה
- 3.10 שאלה 7.10
- 3.11 שאלה
- 3.12 שאלה על מימדים
- 3.13 שאלה כללית
- 3.14 שאלה
- 3.15 שאלה
- 3.16 שאלה 2 בדף המצורף
- 3.17 שאלה 6.4א
- 3.18 שאלה 3 ב בבוחן
- 3.19 שאלה 1 ב' בבוחן
הוראות
כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחילת הדף את השורה הבאה:
== כותרת לשאלה ==
לכתוב מתחתיה את שאלתכם, וללחוץ על שמירה למטה מימין
הודעה חשובה !!! - יש להגיש את התרגילים הנוספים (13 , ו 14 כרשות למי שמגיש ) עד ,וכולל , 16.9.2010 ! למשל לתא הבודקת הילה הלוי בכר , או לתומר ביום רביעי או לניר ביום חמישי - בתרגולי החזרה . אנא הודיעו למי שאתם יודעים שלא יגיע לתרגולים אלו . תודה:)
ארכיון
ארכיון 1 - תרגיל 1
ארכיון 2 - תרגיל 2
ארכיון 3 - בוחן + תרגיל 3
ארכיון 4 - תרגיל 3
שאלות
לכל בסיס של V (מ"ו מסוים) יש אותו מספר איברים
בהוכחה של מה שכתבתי בכותרת, לוקחים B1 בסיס של V עם n איברים, ו-B2 בסיס של V ומוכיחים שגם בו n איברים. בהתחלה מוכיחים שיש ב-B2 לכל היותר n איברים.
לאחר מכן אומרים שאם B2 מכיל פחות מ-n איברים אז B1 תלוי לינארית. למה?
תודה מראש!
שאלה בדירוג מטריצה לבדיקת תלות לינארית
כשמדרגים מטריצה לבדיקת תלות לינארית של איברים, אם מגיעים לשורת אפסים זה אומר שהאיברים הם בת"ל או ת"ל? רק כדי להיות בטוח. תודה רבה!
תשובה
ת"ל לינארית כמובן. כי זה אומר שיש צירוף לינארי לא טריוויאלי של השורות שהתאפס (וגם שמימד מרחב השורות קטן ממספר האיברים בקבוצה ולכן בהכרח היא ת"ל).
- תודה על הכל!
דרך הפתרון ל7.9
איך צריכים לפתור את השאלה? האם צריך להגיד ש (x1,x2,x3,x4,x5) = a(1,2,3,4,5) +b(5,4,3,2,1)+... ואז להראות שיש פתרון כללי ולכן הקבוצה הנתונה פורשת את R5? או שיש דרך אחרת יותר קלה? תודה.
תשובה
למדנו שלמטריצות שקולות שורה יש את אותו מרחב שורה. מספיק לשים את הוקטורים בשורות מטריצה ולדרג.
למדנו גם שהשורות השונות מאפס בצורה המדורגת של המטריצה מהוות בסיס למרחב השורות (זה לצורך חישוב מימד במקרה הזה, כי מבקשים בסיס שמוכל בבסיס המקורי, ולא בסיס כלשהו).
- תודה. אבל תמיד מדרגים מטריצה כדי לבדוק תלות לינארית, לא האם קבוצה היא פורשת! הצלחתי בעזרת דירוג לפתור את ב', אך איך אנמק שהחמישיות פורשות את R5 בעזרת דירוג מטריצות? תודה.
- אם שמת את כל הוקטורים בששת שורות מטריצה, ואחרי דירוג הראת שהמטריצה פורשת את
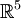 הרי שששת הוקטורים פורסים את המרחב גם. לפי השלישי חינם כל 5 וקטורים בת"ל ב
הרי שששת הוקטורים פורסים את המרחב גם. לפי השלישי חינם כל 5 וקטורים בת"ל ב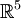 פורשים אותו.
פורשים אותו.
- אה נכון, בעזרת השלישי חינם! תודה וסליחה על בוֹרוּת.
- אם שמת את כל הוקטורים בששת שורות מטריצה, ואחרי דירוג הראת שהמטריצה פורשת את
בקשה
אני מבקש מכל מי ששואל שאלה\עונה תשובה לעשות את הכותרת שלו בדרגה 2, כלומר כך למשל: '==שאלה==' ולא כך: '=שאלה=' אחרת זה משרשר חדש(כי זה בדרגת כותרת של '=שאלות='), וזה נורא מציק לעין, תודה!
שאלה על בסיסים ומ"וים
האם ניתן להגיד (או האם זה נכון בכלל) שאם ל2 מרחבים וקטוריים יש בדיוק את אותו בסיס מסוים, (כלומר מצאתי קבוצה שהיא בסיס לשניהם) אזי המרחבים זהים (הם אותו מרחב וקטורי)? אם כן, האם אפשר לכתוב את זה בלי הוכחה או שצריך לכתוב הוכחה? אם צריך לכתוב הוכחה, איך מוכיחים את זה? תודה רבה.
תשובה
זה טריוויאלי, אבל אם אתה רוצה להוכיח:
B בת"ל בסיס לV אם"ם spanB=V (לפי הגדרה). אם בנוסף B בסיס לU אזי spanB=U מכאן נובע V=U.
- תודה!
שאלה
האם הסקלרים בכל צירוף לינארי כלשהוא חייבים להיות גדולים מאחד? (ובפרט בצירופים הלינאריים שבspan?)
תשובה
בשום צורה לא. הסקלרים הם סקלרים כלשהם מהשדה.
שאלה
האם כל span כולל את אפס?
תשובה
כן כל span הוא תת מרחב וקטורים.
הסבר אחר: span הוא אוסף כל הצירופים הלינאריים, בפרט הצ"ל הטריוויאלי - כלומר כל הסקלרים הם אפסים
7.20
אפשר קצת הסבר על השאלה? אני לא יודע איך להסתכל על זה..מה עוזר לי הנתון שV מ"ו מעל שדה F?ואיך זה בדיוק מתקשר למימד?? אם אפשר קצת רמזים..
תשובה
תמיד חשוב לזכור את ההגדרות - מימד הוא מספר האיברים בבסיס.
אני אתן דוגמא, מקווה שזה יעזור:
ניקח 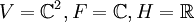 . אפשר לראות שF הוא מרחב וקטורי מעל H עם הבסיס
. אפשר לראות שF הוא מרחב וקטורי מעל H עם הבסיס 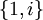 שכן כל מספר מרוכב הוא מהצורה
שכן כל מספר מרוכב הוא מהצורה 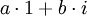 כאשר a,b ממשיים ובוודאי הסכום הזה מתאפס רק אם a=b=0. לכן הקבוצה הנ"ל פורשת ובת"ל ולכן היא בסיס. לכן F הוא ממימד 2 מעל H (כי יש 2 איברים בבסיס).
כאשר a,b ממשיים ובוודאי הסכום הזה מתאפס רק אם a=b=0. לכן הקבוצה הנ"ל פורשת ובת"ל ולכן היא בסיס. לכן F הוא ממימד 2 מעל H (כי יש 2 איברים בבסיס).
V הוא הוא ממימד 2 מעל F (זה ברור). נמצא לו בסיס מעל H: 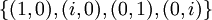 ואכן אנו רואים שV הוא ממימד 4=2x2 מעל H.
ואכן אנו רואים שV הוא ממימד 4=2x2 מעל H.
שאלה
אם אני יודע ש:
v מרחב וקטורי נוצר סופית, ובנוסף:
ובנוסף:
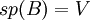
- B בת"ל.
אז אני יכול להגיד ש-B בסיס עבור V?
תשובה
כן. זו ההגדרה של בסיס. Span(B)=V (פורש) ובת"ל
שאלה 7.10
העברתי את המטריצות לעמודות, ודירגתי את המטריצה שהתקבלה. יצאו לי ארבע שורות אפסים, האם זה אומר שהן תלויות לינארית ? איך מנמקים את זה?
תשובה
השאלה היא לא כמה שורות אפסים יש, אלא כמה משתנים חופשיים יש. אם קיים פתרון לא טריוויאלי למערכת Ax=0 אזי עמודות A תלויות לינארית.
שאלה
איך מוכיחים שקבוצה היא פורשת? ואיך מוצאים בסיס לקבוצה?
תשובה
למדנו שמרחבי השורות של מטריצות שקולות שורה הם זהים. לכן על מנת למצוא בסיס לקבוצת וקטורים יש לשים אותם בשורות מטריצה ולדרג את המטריצה. בצורה המדורגת של המטריצה, השורות השונות מאפס מהוות בסיס למרחב השורות.
הspan של הקבוצה הוא כמובן הspan של השורות השונות מאפס בצורה המדורגת. כך ניתן לדעת מה הקבוצה פורשת (קבוצה תמיד פורשת את הspan שלה - זו ההגדרה).
כאשר יש מרחב וקטורי של פולינומים או מטריצות - מעבירים אותו לצורה וקטורית פשוטה כמו בתרגיל לדוגמא שפרסמנו בעמוד הראשי.
שאלה על מימדים
מה המימד של המרחב הוקטורי המכיל רק 0? האם סכום ישר אומר שהחיתוך נותן 0? כי אם כך אז המימד של {(a,b,0,0) סכום ישר (0a,0,d,c)} שווה לסכום המימדים שהוא 4, פחות מימד החיתוך שהוא 1, לא? אזי מימד הסכום שווה ל3 אבל הוא באמת שווה ל-4. מה הולך פה?
תשובה
המימד של מרחב האפס {0} הוא אפס. הבסיס שלו הוא הקבוצה הריקה.
שאלה כללית
האם שורותיה של מטריצה בדורגת הם בהכרח בת"ל?
תשובה
שורותיה השונות מאפס של מטריצה מדורגת הן בהכרח בת"ל. אף שורה איננה צ"ל של קודמותיה, כי יש לה אפסים במקומות בהם יש לשורות הקודמות איברים פותחים.
שאלה
האם אני יכול להגיד את הדבר הבא?
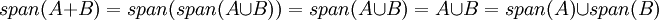 תודה מראש...
תודה מראש...
תשובה
לא. האיחוד של תתי מרחבים לרוב אינו תת מרחב. שאלה זו מופיעה בתרגיל 3, והפרכתה נמצאת בפתרונות.
המעבר הראשון הלא חוקי (משמאל לימין) הוא שאפשר להוריד את הspan ולהשאיר שיוויון. מה פתאום הspan של קבוצה שווה לקבוצה? הרי הקבוצה יכולה להיות סופית, ואוסף כל הצירופים הלינאריים הוא אינו סופי (מעל שדה אינסופי כמובן)
שאלה
1.אם (V1,v2...vn) וקטורים בת"ל וגם (u1,u2,...,un) וקטורים בת"ל ומתקיים ש: v1=a1u1+a2u2...anun,...,vn=b1u1+b2u2+...+bnun , אני יכולה להגיד ש {a1,...,an}..{b1,...,bn הם בת"ל?
2. מטריצת מעבר היא חייבת להיות ריבועית?
תשובה
1. סקלרים לא יכולים לעולם להיות בת"ל. ההגדרה של בת"ל תקפה רק לגבי וקטורים.
2. כן. כי הרי יש בה n עמודות (מספר האיברים בבסיס B) שכל אחת מהן באורך n (מספר האיברים בבסיס C). הרי מספר האיברים זהה בכל הבסיסים.
- לגבי 1. אני לא מבינה! הרי כן אפשר להסתכל על כוקטורי עמודה {a1,..,an},{b1,...,bn ולשאול האם הם תלויים לינארית?
- הסימון עם סוגריים מסולסלים מסמן קבוצה, ולא וקטור עמודה. את מתכוונת ל
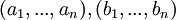 ? (כלומר, 2 וקטורי קואורדינטות) אה.. אני בכלל מבין עכשיו את הטעות בסימון. מהם הסקלרים שבין a ל b?
? (כלומר, 2 וקטורי קואורדינטות) אה.. אני בכלל מבין עכשיו את הטעות בסימון. מהם הסקלרים שבין a ל b?
- הסימון עם סוגריים מסולסלים מסמן קבוצה, ולא וקטור עמודה. את מתכוונת ל
- אני מניח שהתכוונת ל
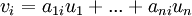 ואז השאלה אם הקבוצה
ואז השאלה אם הקבוצה 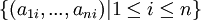 היא בת"ל. אבל זה בדיוק השאלה בשיעורי הבית. צריך להוכיח את זה.
היא בת"ל. אבל זה בדיוק השאלה בשיעורי הבית. צריך להוכיח את זה.
- רמז: ההעתקה מv לקואורדינטות של v לפי בסיס מסוים, הינה העתקה לינארית.
שאלה 2 בדף המצורף
כל מספר מסוים של וקטורים מתוך מרחב מסוים שהם בת"ל הם בהכרח גם בסיס של אותו המרחב?
תשובה
בוודאי שלא. בסיס הוא פורש וגם בת"ל. אחד התנאים בלבד אינו מספיק. מספר הוקטורים היחיד שיכול להיות בבסיס הוא המימד של המרחב.
לדוגמא:
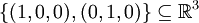 בת"ל אבל לא בסיס.
בת"ל אבל לא בסיס.
אבל (ואולי לזה התכוונת) אם ניקח קבוצה בת"ל עם מספר וקטורים כגודל המימד של המרחב היא אכן תהיה בסיס תודות למשפט השלישי חינם.
שאלה 6.4א
בשאלה מבקשים לוהכיח שאם חיתוך של שני ספאנים שונה מאפס, אבל כל ספאן יוצר צירוף לינארי מתאפס, אז הטענה בכלל לא יכולה להיות נכונה, האם זה בעיה בתרגיל?
תשובה
שאלה על התשובה
את/ה יכול/ה לתת דוגמא ל2 קבוצות שמקיימות את התנאי הזה?
דוגמא
ניקח 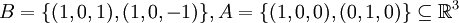
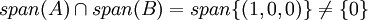
במילים: יש צירוף לינארי של A וצירוף לינארי של B ששניהם שווים זה לזה אבל שונים מאפס.
שאלה 3 ב בבוחן
שלום, לא הבנתי למה הזווית של 1+i היא בדיוק פי חלקי ארבע? מה החישוב שעושים?
תשובה
במישור המרוכב זו הנקודה (1,1) שנמצאת בדיוק על הקו הישר x=y שנמצא בזוית 45 מעלות (כי הוא חוצה את הזוית הישרה בין הצירים). אם זה לא מספיק ברור, גם 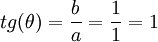 ולכן
ולכן 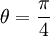
שאלה 1 ב' בבוחן
בפתרונות כתוב שאם נדרג נמצא שורת סתירה עבור a=0ולכן אין פיתרון. דרגתי כמה וכמה פעמים ואני לא מוצאת שום שורת סתירה! אני כן מחלקת בa כחלק מהפעולות אלמנטריות אבל כשאני רוצה להוכיח שבאמת אין פיתרון עבור a=0 אני לא מצליחה! אתה יכול לפרט יותר?
תשובה
אסור לחלק בa כחלק מהפעולות האלמנטריות כאשר בודקים את המקרה a=0 זה מקור הטעות.
תציבי במטריצה המקורית a=0 ותראי לאן את מגיעה. אוקי תודה!