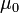השראה אלקטרומגנטית
בתחילה, תופעות חשמליות ותופעות מגנטיות נחשבו בלתי תלויות אלה באלה. הקשר בין חשמל למגנטיות נתגלה ע"י ארסטד (Oersted) בשנת 1820. קיימת אגדה, לפיה הגילוי נעשה במהלך הרצאה, שארסטד ערך כדי להציג לסטודנטים את חוסר התלות בין חשמל למגנטיות. סטודנט מצטיין, שעקב בזהירות אחר הניסויים בהרצאה, שם לב לסטייה קטנה של מחט המצפן, כשמקרבים מצפן לתיל נושא זרם חשמלי. כך נתגלה, כי זרם חשמלי יוצר שדה מגנטי במרחב מסביב. כיום ידוע, כי שדה מגנטי נוצר ע"י זרם חשמלי, אף שזרם זה, לעיתים, אינו ניתן למדידה ישירה (כדוגמת השדה המגנטי של כדור-הארץ או של מגנט קבוע). לאחר גילוי זה, המדענים החלו לחפש אחר אפקט הפוך – יצירת זרם חשמלי באמצעות שדה מגנטי. חיפושים אלה לא הניבו תוצאות במשך שנים רבות. הסיבה לכך פשוטה: רק שינויים בשדה מגנטי גורמים ליצירת שדה חשמלי. תופעה זו, נקראת בשם השראה אלקטרומגנטית, נתגלתה לראשונה ע"י פרדיי (Faraday) בשנת 1831.
מחולל זרם (גנרטור) הוא מתקן ליצירת אנרגיה חשמלית המהווה כיום את אחד מיסודות הציוויליזציה, ויותר מ- 99% מאנרגיה זו מופקים בעזרת חוק ההשראה האלקטרומגנטית. על כן, ניתן להשוות גילוי תופעה זו להמצאת הגלגל או לגילוי אמריקה.
במעבדה זו נחקור את התלות בין התופעות החשמליות למגנטיות ונקבל מתוך המדידות את גודלו של קבוע פיסיקאלי חשוב, מקדם הפרמאביליות של הריק, 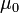 .
.
רקע תיאורטי
חוק ההשראה האלקטרומגנטית (חוק פרדיי) אומר, שהכא"מ המושרה 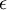 פרופורציוני לקצב השינוי בשטף המגנטי,
פרופורציוני לקצב השינוי בשטף המגנטי, 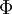 העובר דרך מעגל חשמלי, כלומר:
העובר דרך מעגל חשמלי, כלומר:
 .
.
מערכת הניסוי
במעבדה הנוכחית, שדה מגנטי נוצר באמצעות סליל ארוך – סולנואיד (ציור 1). שדה מגנטי במרכז סליל זה הוא אחיד ושווה ל- 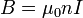 כאשר
כאשר 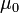 - קבוע הנקרא פרמאביליות הריק,
- קבוע הנקרא פרמאביליות הריק,  - מספר הליפופים בסליל ליח' אורך,
- מספר הליפופים בסליל ליח' אורך, 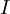 - עוצמת הזרם בסליל. כל הגדלים יוצגו ביחידות של SI (טסלה, מטר, אמפר).
- עוצמת הזרם בסליל. כל הגדלים יוצגו ביחידות של SI (טסלה, מטר, אמפר).
נעביר דרך הסליל זרם חילופין בתדירות 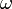
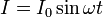 , ממקור משתנה, הנמדד ע"י מולטימטר.
במקרה זה השדה המגנטי בתוך הסליל יהיה
, ממקור משתנה, הנמדד ע"י מולטימטר.
במקרה זה השדה המגנטי בתוך הסליל יהיה
.
כאשר, 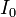 היא האמפליטודה של זרם החילופין בסליל.
בתוך הסולנואיד, סמוך למרכזו, נמקם סליל משני. השטף המגנטי העובר דרך סליל זה הוא:
היא האמפליטודה של זרם החילופין בסליל.
בתוך הסולנואיד, סמוך למרכזו, נמקם סליל משני. השטף המגנטי העובר דרך סליל זה הוא:
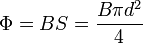 כאשר
כאשר 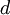 - קוטר הסליל המשני.
- קוטר הסליל המשני.
הכא"מ המושרה בסליל המשני לפי חוק פרדי הוא:
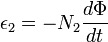 כאשר
כאשר 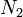 הוא מספר הליפופים בסליל המשני.
את הכא"מ המושרה נמדוד באמצעות מולטימטר או באמצעות סקופ.
כדאי לשים לב לכך שהשדה מגנטי של סולנואיד קטן יותר ליד הקצוות שלו.
הוא מספר הליפופים בסליל המשני.
את הכא"מ המושרה נמדוד באמצעות מולטימטר או באמצעות סקופ.
כדאי לשים לב לכך שהשדה מגנטי של סולנואיד קטן יותר ליד הקצוות שלו.
הערה: מכשירים, המודדים זרם או מתח חילופין, מראים את הערכים האפקטיביים  ו-
ו- 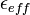 , והם קטנים עבור זרם סינוס פי
, והם קטנים עבור זרם סינוס פי 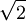 ביחס לאמפליטודה.
ביחס לאמפליטודה.
מערכת הניסוי מוצגת באיור 1, כאשר לסליל הפנימי קוטר של  ו - 300 ליפופים. לסולנואיד:
ו - 300 ליפופים. לסולנואיד: 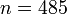 (מספר ליפופים למטר).
(מספר ליפופים למטר).
הסליל הארוך (סולנואיד) מחובר למחולל האותות שמופעל דרך המחשב, כאשר זרם החילופין שעובר דרך הסולנואיד נמדד ע"י האופציה במחשב - Output current. נגד מחובר בטור לסולנואיד, ולכן הזרם הוא כמעט בלתי תלוי בתדירות. Voltage sensor ימדוד את הכא"מ המושרה (מתח AC) בסליל הקטן.
מהלך הניסוי
- הרכיבו את מערכת הניסוי שבאיור 1. כמקור מתח חילופין ישמש מחולל האותות מהממשק.
- מדדו את המתח בסליל המשני כפונקציה של תדר המחולל, כאשר הזרם הוא חילופין באמפליטודה
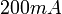 . בצעו מדידות בטווח של
. בצעו מדידות בטווח של 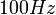 עד
עד 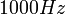 בקפיצות של
בקפיצות של 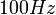 .
.
- בתדר של
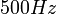 שנו את אמפליטודת המחולל בין ערך מינימום למקסימום ומדדו את המתח בסליל המשני כפונקציה של הזרם בסליל הראשי.
שנו את אמפליטודת המחולל בין ערך מינימום למקסימום ומדדו את המתח בסליל המשני כפונקציה של הזרם בסליל הראשי.
- שרטטו את התוצאות בגרפים.
- מצאו את הקבוע