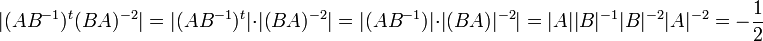88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/11
דטרמיננטות
הגדרה הדטרמיננטה של מטריצה ריבועית 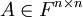 היא סקלר
היא סקלר 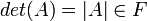 המחושב מסכומים של מכפלות של אברי המטריצה.
המחושב מסכומים של מכפלות של אברי המטריצה.
חישוב דטרמיננטה של מטריצות קטנות
- הדטרמיננטה של מטריצה מסדר 1
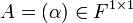 היא הערך היחיד במטריצה
היא הערך היחיד במטריצה 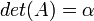 .
.
- הדטרמיננטה של מטריצה עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): A=\pmatrix{a&b\\ c&d} \in F^{2\times 2}
היא.
למשל: עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): det\pmatrix{1&2\\ 3&4} = 1\cdot 4-2\cdot 3=-2 .
חישוב לפי נוסחת לפלס (מינורים)
סימון עבור מטריצה 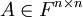 נסמן ב
נסמן ב 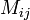 את המטריצה מגודל
את המטריצה מגודל 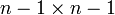 המתקבלת מ
המתקבלת מ ע"י מחיקת השורה ה
ע"י מחיקת השורה ה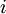 והעמודה ה
והעמודה ה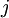 . זה נקרא המינור ה
. זה נקרא המינור ה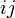 של המטריצה.
של המטריצה.
דוגמא: עבור עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): A=\pmatrix{1&2&3\\ 4&5&6\\ 7&8&9}
למשל
עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): M_{12}=\pmatrix{4&6\\ 7&9}
עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): M_{23}=\pmatrix{1&2\\ 7&8}
אפשר למצוא את הדטרמיננטה בעזרת הדטרמיננטות של המינורים (לפי שורה או לפי עמודה), וכך באינדוקציה למצוא דטורמיננטה של כל מטריצה.
מציאת הדטרמיננטה ע"י מינורים עם פיתוח לפי השורה ה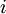 :
:
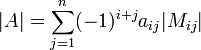
מציאת הדטרמיננטה ע"י מינורים עם פיתוח לפי העמודה ה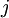 :
:
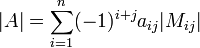
לדוגמא: עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): A=\pmatrix{1&2&3\\ 4&5&6\\ 7&8&9}
נפתח לפי השורה הראשונה:
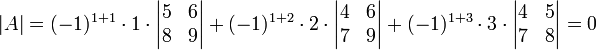
נפתח גם לפי העמודה השנייה:
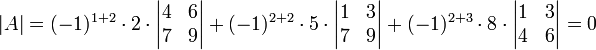
תכונות של הדטרמיננטה
1. כפליות 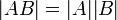 .
.
2. בפרט 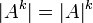 .
.
3. 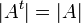 .
.
4. אם המטריצה משולשית אז הדטרמיננטה= מכפלת אברי האלכסון (להדגים?).
5. אם  הפיכה אז
הפיכה אז 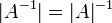 .
.
6.  הפיכה אם"ם
הפיכה אם"ם 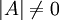 .
.
למשל המטריצה עיבוד הנוסחה נכשל (פונקציה \pmatrix לא מוכרת): A=\pmatrix{1&2&3\\ 4&5&6\\ 7&8&9}
איננה הפיכה כי חישבנו שהדטרמיננטה היא אפס.
שימו לב שאין בהכרח קשר בין 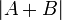 לבין
לבין 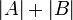 . (דוגמא?)
. (דוגמא?)
תרגיל
נתונות מטריצות 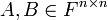 כך ש
כך ש 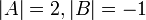 . חשבו את
. חשבו את 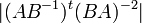 .
.
פתרון