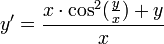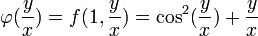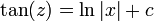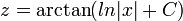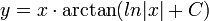מד"ר - משוואות דיפרנציאליות רגילות - ארז שיינר
מתוך Math-Wiki
תוכן עניינים
הרצאה 1 הקדמה ומשוואה פרידה
- משוואה דיפרנציאלית מכילה את המשתנה, הפונקציה ונגזרותיה.
- בחקירת פונקציות, במציאת תחומי עלייה וירידה, אנו פותרים את המשוואה
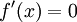 . האם זו משוואה דיפרנציאלית?
. האם זו משוואה דיפרנציאלית? - לא, כיוון שבמשוואות דיפרנציאלית אנו מחפשים פונקציה שמקיימת את המשוואה לכל ערך של המשתנה.
- כאן הפונקציה נתונה, ואנו מחפשים ערך של המשתנה שמקיים את המשוואה.
נפילה חופשית
- גוף הנופל חופשית נופל בתאוצה שבקירוב היא קבועה
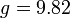 .
. - נסמן ב
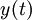 את הגובה של הגוף (כאשר הכיוון החיובי הוא לכיוון כדור הארץ)
את הגובה של הגוף (כאשר הכיוון החיובי הוא לכיוון כדור הארץ) 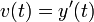 היא המהירות
היא המהירות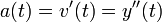 היא התאוצה.
היא התאוצה.- לכן על מנת לדעת את מיקומו של הגוף בכל נקודה בזמן, עלינו לפתור את המשוואה
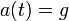 , הרי התאוצה קבועה.
, הרי התאוצה קבועה.
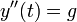
- לכן
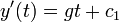
- לכן
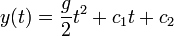
- כיצד נחשב את הקבועים? לפי תנאי ההתחלה.
- נסמן את הגובה ההתחלתי בתור 0 (נזכור כי הכיוון החיובי הוא לכיוון כדור הארץ). ולכן
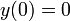 ולכן
ולכן 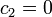
- נניח כי המהירות ההתחלתית גם היא הייתה 0 ולכן
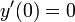 ולכן גם
ולכן גם 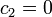 .
.
ריבית דריבית
- נניח שסכום הכסף בבנק לאורך זמן מתואר על ידי הפונקציה
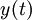 .
. - נניח שאנו מרוויחים תשואה של 2 אחוז בשנה, לכן לאחר שנה יתקיים כי
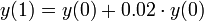 .
. - אבל מה היה קורה אילו הבנק היה משלם את הריבית פעם בחצי שנה?
- בחצי השנה הראשונה נקבל מחצית מהריבית
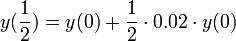
- ובחצי השנה השנייה נקבל מחצית מהריבית, אך סכום הקרן שלנו כבר גדל
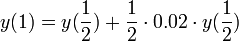
- סה"כ
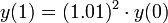
- בחצי השנה הראשונה נקבל מחצית מהריבית
- זה גדול יותר מהריבית השנתית, כיוון שצברנו ריבית על הקרן וגם על הריבית החצי שנתית.
- האם יש דרך להפוך את התהליך לרציף?
- כלומר, בהנתן שתי נקודות זמן קרובות אנו מעוניינים לקבל את הריבית היחסית על הזמן שעבר:
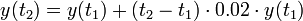
- נעביר אגף ונחלק
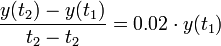
- אם נשאיף
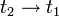 נקבל כי
נקבל כי 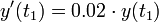
- כלומר אנו מעוניינים בפונקציה שמקיימת את המשוואה הדיפרנציאלית
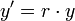 כאשר
כאשר 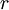 היא הריבית השנתית.
היא הריבית השנתית.
המשוואה 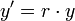
- בהמשך הקורס נעסוק בשאלה האם למשוואה דיפרנציאלית יש פתרון, וכמה פתרונות יש למשוואה.
- מידי פעם נחזור ונפתור את המשוואה הזו בכלים שונים.
- כעת נשים לב כי:
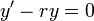
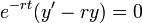
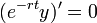
- כיוון שהנגזרת שווה אפס הפונקציה קבועה
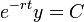
- סה"כ
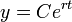
- על מנת לחשב את הקבוע C עבור המקרה של ריבית דריבית, עלינו לדעת כמה כסף היה בחשבון בזמן t=0.
- שימו לב שלכל תנאי התחלה קיבלנו פתרון יחיד.
סדר ומעלה
- משוואה דיפרנציאלית נקראת מסדר n אם הנגזרת הגבוהה ביותר היא מסדר n.
- המשוואה
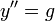 היא משוואה מסדר שני.
היא משוואה מסדר שני. - המשוואה
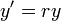 היא משוואה מסדר ראשון.
היא משוואה מסדר ראשון.
- המשוואה
- משוואה דיפרנציאלית נקראת ממעלה n אם הנגזרת מהסדר הגבוה ביותר היא ממעלה n.
- המשוואה
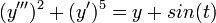 היא מסדר 3 ומעלה 2.
היא מסדר 3 ומעלה 2.
- המשוואה
משוואות פרידות
- משוואה דיפרנציאלית נקראת פרידה אם היא מהצורה
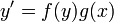 .
. - נהוג גם להחליף
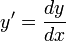 ולכן המשוואה תרשם כך
ולכן המשוואה תרשם כך 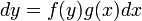 .
. - לבסוף, אם נזהר עם חלוקה באפס, משוואה פרידה באופן כללי יכולה להיות מהצורה
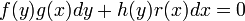 , כלומר
, כלומר 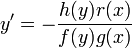 .
.
- משוואות פרידות אנו יכולים לפתור באמצעות אינטגרלים באופן הבא:
- ראשית נפריד (ומכאן השם) את המשתנים לשני צידי המשוואה:
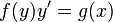
- הקדומות של שני הצדדים שוות עד כדי קבוע.

- במקום t נשאר עם המשתנה y ובעצם אנו מחשבים אינטגרלים לשני הצדדים
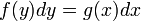 , כל אחד לפי המשתנה שלו!
, כל אחד לפי המשתנה שלו!
- לדוגמא נפתור את המשוואה
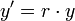 כמשוואה פרידה.
כמשוואה פרידה. - ראשית נפריד את המשתנים ונקבל כי
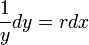 .
. - נשים לב כי הנחנו כאן כי
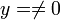 .
. - כעת
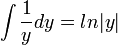 .
. 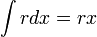 .
.- וביחד
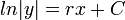 .
. - לכן
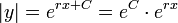 .
. - לכן
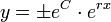 .
. - כעת, קל לראות מהצבה במשוואה כי y=0 גם פותר את המשוואה.
- בסה"כ הפתרון הכללי הוא (שוב)
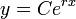 .
.
- שימו לב - חלקנו למקרים בהם הפונקציה שונה מאפס או קבועה אפס, אך לא טיפלנו במקרים בהם הפונקציה מידי פעם שווה אפס.
- בתרגיל זה איננו צריכים, כי מצאנו את הפתרון הכללי בדרך פשוטה יותר למעלה.
- בהמשך, משפט הקיום והיחידות יעזור לנו להתמודד עם השאלה הזו, אך באופן כללי לא נעסוק הרבה במקרי קצה בקורס זה.
הפיכת משוואה לפרידה
- נביט במשוואה
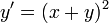 שאינה משוואה פרידה.
שאינה משוואה פרידה. - נדגים עכשיו טריק שיהפוך את המשוואה לפרידה.
- נגדיר את הפונקציה
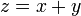 .
. - מתקיים כי
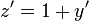 וביחד המשוואה המקורית מקבלת את הצורה
וביחד המשוואה המקורית מקבלת את הצורה 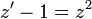 .
. - זוהי משוואה פרידה
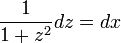 .
. - נפעיל אינטגרל על שני הצדדים ונקבל כי
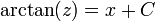
- ולכן
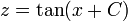
- ולכן

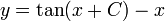
- שימו לב לדוגמא, כאן לא התייחסנו למקרה הקצה בו
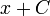 מחוץ לתחום
מחוץ לתחום 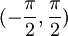 .
. - שיטה אחת לוודא שהפתרון שלנו אכן נכון היא להציב את התוצאה שקיבלנו ישירות במשוואה.
- על מנת לדעת אם לא פספסנו פתרונות אחרים, נעזר בהמשך במשפט הקיום והיחידות.
- אבל כאמור - אנחנו לא נתייחס באופן כזה לכל מקרה קצה בהמשך הקורס.
הרצאה 2 מד"ר הומוגנית ומד"ר לינאריות מסדר ראשון
מד"ר הומוגנית
- פונקציה
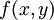 נקראת הומוגנית מסדר k אם לכל
נקראת הומוגנית מסדר k אם לכל 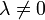 מתקיים כי
מתקיים כי 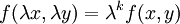 .
. - לדוגמא
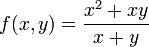 הומוגנית מסדר 1.
הומוגנית מסדר 1.
- טענה: פונקציה
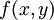 היא מהצורה
היא מהצורה  לכל
לכל 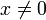 אם"ם היא הומוגנית מסדר
אם"ם היא הומוגנית מסדר 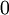 לכל
לכל 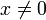 .
. - הוכחה:
- אם
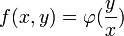 אזי לכל
אזי לכל 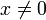 מתקיים
מתקיים  .
. - אם
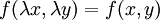 , נציב
, נציב 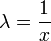 ונקבל כי
ונקבל כי 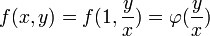 .
.
- אם
- מד"ר הומוגנית (בניגוד למד"ר לינארית הומוגנית שנראה בהמשך) היא משוואה מהצורה
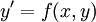 כאשר
כאשר 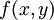 הומוגנית מסדר
הומוגנית מסדר  .
. - נפתור מד"ר הומוגנית באמצעות ההצבה
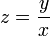 באופן הבא:
באופן הבא:
- ראשית נסמן
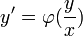 .
. - כעת נגזור את שני צידי המשוואה
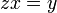 , ונקבל כי
, ונקבל כי 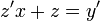 .
. - לכן לאחר החלפת המשתנה קיבלנו משוואה פרידה
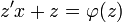 .
. - נפריד את המשתנים
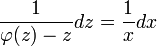 .
. - ולכן
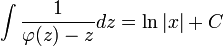 .
. - נמצא את
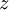 ונציב בחזרה
ונציב בחזרה 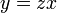 .
.
- ראשית נסמן
- דוגמא - נפתור את המשוואה
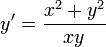
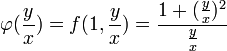

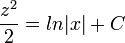
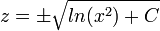
- ולבסוף
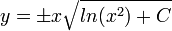
- דוגמא - נפתור את המשוואה
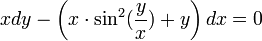
מד"ר לינארית מסדר ראשון
- הגדרה: משוואה מסדר ראשון נקראת לינארית אם היא מהצורה
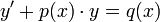 .
. - מד"ר לינארית הומוגנית (בניגוד למד"ר הומוגנית שראינו לעיל) היא מהצורה
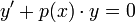 .
. - נחשב נוסחא לפתרון מד"ר לינארית כללית ע"י מציאת פתרון למשוואה לינארית הומוגנית ובאמצעות שיטת וריאצית המקדמים.