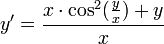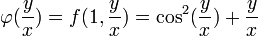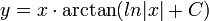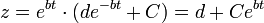מד"ר - משוואות דיפרנציאליות רגילות - ארז שיינר
מתוך Math-Wiki
תוכן עניינים
הרצאה 1 הקדמה ומשוואה פרידה
- משוואה דיפרנציאלית מכילה את המשתנה, הפונקציה ונגזרותיה.
- בחקירת פונקציות, במציאת תחומי עלייה וירידה, אנו פותרים את המשוואה
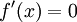 . האם זו משוואה דיפרנציאלית?
. האם זו משוואה דיפרנציאלית? - לא, כיוון שבמשוואות דיפרנציאלית אנו מחפשים פונקציה שמקיימת את המשוואה לכל ערך של המשתנה.
- כאן הפונקציה נתונה, ואנו מחפשים ערך של המשתנה שמקיים את המשוואה.
נפילה חופשית
- גוף הנופל חופשית נופל בתאוצה שבקירוב היא קבועה
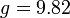 .
. - נסמן ב
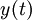 את הגובה של הגוף (כאשר הכיוון החיובי הוא לכיוון כדור הארץ)
את הגובה של הגוף (כאשר הכיוון החיובי הוא לכיוון כדור הארץ) 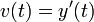 היא המהירות
היא המהירות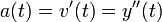 היא התאוצה.
היא התאוצה.- לכן על מנת לדעת את מיקומו של הגוף בכל נקודה בזמן, עלינו לפתור את המשוואה
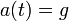 , הרי התאוצה קבועה.
, הרי התאוצה קבועה.
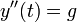
- לכן
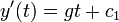
- לכן
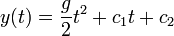
- כיצד נחשב את הקבועים? לפי תנאי ההתחלה.
- נסמן את הגובה ההתחלתי בתור 0 (נזכור כי הכיוון החיובי הוא לכיוון כדור הארץ). ולכן
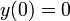 ולכן
ולכן 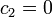
- נניח כי המהירות ההתחלתית גם היא הייתה 0 ולכן
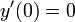 ולכן גם
ולכן גם 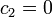 .
.
ריבית דריבית
- נניח שסכום הכסף בבנק לאורך זמן מתואר על ידי הפונקציה
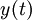 .
. - נניח שאנו מרוויחים תשואה של 2 אחוז בשנה, לכן לאחר שנה יתקיים כי
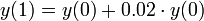 .
. - אבל מה היה קורה אילו הבנק היה משלם את הריבית פעם בחצי שנה?
- בחצי השנה הראשונה נקבל מחצית מהריבית
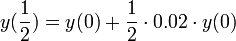
- ובחצי השנה השנייה נקבל מחצית מהריבית, אך סכום הקרן שלנו כבר גדל
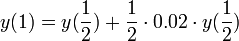
- סה"כ
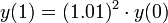
- בחצי השנה הראשונה נקבל מחצית מהריבית
- זה גדול יותר מהריבית השנתית, כיוון שצברנו ריבית על הקרן וגם על הריבית החצי שנתית.
- האם יש דרך להפוך את התהליך לרציף?
- כלומר, בהנתן שתי נקודות זמן קרובות אנו מעוניינים לקבל את הריבית היחסית על הזמן שעבר:
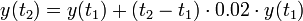
- נעביר אגף ונחלק
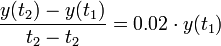
- אם נשאיף
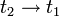 נקבל כי
נקבל כי 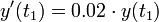
- כלומר אנו מעוניינים בפונקציה שמקיימת את המשוואה הדיפרנציאלית
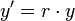 כאשר
כאשר 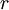 היא הריבית השנתית.
היא הריבית השנתית.
המשוואה 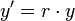
- בהמשך הקורס נעסוק בשאלה האם למשוואה דיפרנציאלית יש פתרון, וכמה פתרונות יש למשוואה.
- מידי פעם נחזור ונפתור את המשוואה הזו בכלים שונים.
- כעת נשים לב כי:
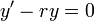
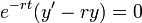
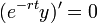
- כיוון שהנגזרת שווה אפס הפונקציה קבועה
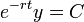
- סה"כ
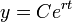
- על מנת לחשב את הקבוע C עבור המקרה של ריבית דריבית, עלינו לדעת כמה כסף היה בחשבון בזמן t=0.
- שימו לב שלכל תנאי התחלה קיבלנו פתרון יחיד.
סדר ומעלה
- משוואה דיפרנציאלית נקראת מסדר n אם הנגזרת הגבוהה ביותר היא מסדר n.
- המשוואה
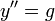 היא משוואה מסדר שני.
היא משוואה מסדר שני. - המשוואה
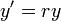 היא משוואה מסדר ראשון.
היא משוואה מסדר ראשון.
- המשוואה
- משוואה דיפרנציאלית נקראת ממעלה n אם הנגזרת מהסדר הגבוה ביותר היא ממעלה n.
- המשוואה
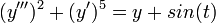 היא מסדר 3 ומעלה 2.
היא מסדר 3 ומעלה 2.
- המשוואה
משוואות פרידות
- משוואה דיפרנציאלית נקראת פרידה אם היא מהצורה
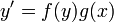 .
. - נהוג גם להחליף
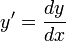 ולכן המשוואה תרשם כך
ולכן המשוואה תרשם כך 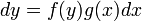 .
. - לבסוף, אם נזהר עם חלוקה באפס, משוואה פרידה באופן כללי יכולה להיות מהצורה
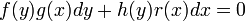 , כלומר
, כלומר 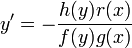 .
.
- משוואות פרידות אנו יכולים לפתור באמצעות אינטגרלים באופן הבא:
- ראשית נפריד (ומכאן השם) את המשתנים לשני צידי המשוואה:
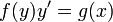
- הקדומות של שני הצדדים שוות עד כדי קבוע.

- במקום t נשאר עם המשתנה y ובעצם אנו מחשבים אינטגרלים לשני הצדדים
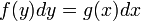 , כל אחד לפי המשתנה שלו!
, כל אחד לפי המשתנה שלו!
- לדוגמא נפתור את המשוואה
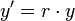 כמשוואה פרידה.
כמשוואה פרידה. - ראשית נפריד את המשתנים ונקבל כי
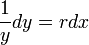 .
. - נשים לב כי הנחנו כאן כי
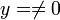 .
. - כעת
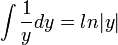 .
. 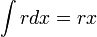 .
.- וביחד
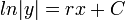 .
. - לכן
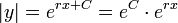 .
. - לכן
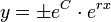 .
. - כעת, קל לראות מהצבה במשוואה כי y=0 גם פותר את המשוואה.
- בסה"כ הפתרון הכללי הוא (שוב)
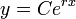 .
.
- שימו לב - חלקנו למקרים בהם הפונקציה שונה מאפס או קבועה אפס, אך לא טיפלנו במקרים בהם הפונקציה מידי פעם שווה אפס.
- בתרגיל זה איננו צריכים, כי מצאנו את הפתרון הכללי בדרך פשוטה יותר למעלה.
- בהמשך, משפט הקיום והיחידות יעזור לנו להתמודד עם השאלה הזו, אך באופן כללי לא נעסוק הרבה במקרי קצה בקורס זה.
הפיכת משוואה לפרידה
- נביט במשוואה
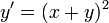 שאינה משוואה פרידה.
שאינה משוואה פרידה. - נדגים עכשיו טריק שיהפוך את המשוואה לפרידה.
- נגדיר את הפונקציה
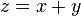 .
. - מתקיים כי
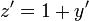 וביחד המשוואה המקורית מקבלת את הצורה
וביחד המשוואה המקורית מקבלת את הצורה 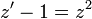 .
. - זוהי משוואה פרידה
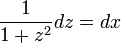 .
. - נפעיל אינטגרל על שני הצדדים ונקבל כי
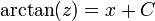
- ולכן
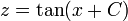
- ולכן

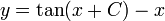
- שימו לב לדוגמא, כאן לא התייחסנו למקרה הקצה בו
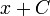 מחוץ לתחום
מחוץ לתחום 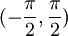 .
. - שיטה אחת לוודא שהפתרון שלנו אכן נכון היא להציב את התוצאה שקיבלנו ישירות במשוואה.
- על מנת לדעת אם לא פספסנו פתרונות אחרים, נעזר בהמשך במשפט הקיום והיחידות.
- אבל כאמור - אנחנו לא נתייחס באופן כזה לכל מקרה קצה בהמשך הקורס.
הרצאה 2 מד"ר הומוגנית, מד"ר לינאריות מסדר ראשון ומשוואת ברנולי
מד"ר הומוגנית
- פונקציה
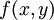 נקראת הומוגנית מסדר k אם לכל
נקראת הומוגנית מסדר k אם לכל 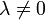 מתקיים כי
מתקיים כי 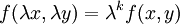 .
. - לדוגמא
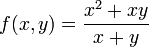 הומוגנית מסדר 1.
הומוגנית מסדר 1.
- טענה: פונקציה
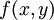 היא מהצורה
היא מהצורה  לכל
לכל 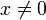 אם"ם היא הומוגנית מסדר
אם"ם היא הומוגנית מסדר 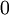 לכל
לכל 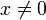 .
. - הוכחה:
- אם
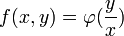 אזי לכל
אזי לכל 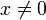 מתקיים
מתקיים  .
. - אם
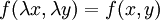 , נציב
, נציב 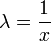 ונקבל כי
ונקבל כי 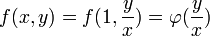 .
.
- אם
- מד"ר הומוגנית (בניגוד למד"ר לינארית הומוגנית שנראה בהמשך) היא משוואה מהצורה
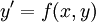 כאשר
כאשר  הומוגנית מסדר
הומוגנית מסדר 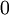 .
. - נפתור מד"ר הומוגנית באמצעות ההצבה
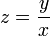 באופן הבא:
באופן הבא:
- ראשית נסמן
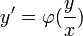 .
. - כעת נגזור את שני צידי המשוואה
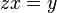 , ונקבל כי
, ונקבל כי 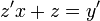 .
. - לכן לאחר החלפת המשתנה קיבלנו משוואה פרידה
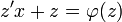 .
. - נפריד את המשתנים
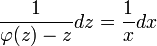 .
. - ולכן
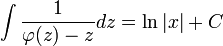 .
. - נמצא את
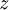 ונציב בחזרה
ונציב בחזרה 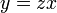 .
.
- ראשית נסמן
- דוגמא - נפתור את המשוואה
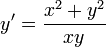
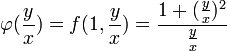

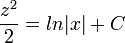
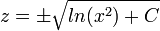
- ולבסוף
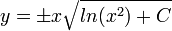
- דוגמא - נפתור את המשוואה
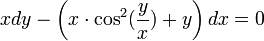
מד"ר לינארית מסדר ראשון
- הגדרה: משוואה מסדר ראשון נקראת לינארית אם היא מהצורה
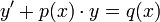 .
. - מד"ר לינארית הומוגנית (בניגוד למד"ר הומוגנית שראינו לעיל) היא מהצורה
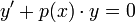 .
. - נחשב נוסחא לפתרון מד"ר לינארית כללית ע"י מציאת פתרון למשוואה לינארית הומוגנית ובאמצעות שיטת וריאצית המקדמים.
- נשים לב כי המשוואה הלינארית ההומוגנית
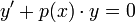 היא פרידה.
היא פרידה. - נפריד את המשתנים ונקבל
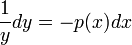 .
. - נבצע אינטגרציה ונקבל כי
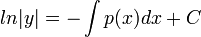 .
. - ולכן
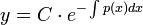
- כעת נשתמש בשיטת וריאצית המקדמים על מנת לפתור את המד"ר הלא הומוגנית.
- נציב במקום המקדם הקבוע
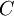 פונקציה
פונקציה  , וננחש שזה פתרון של המד"ר.
, וננחש שזה פתרון של המד"ר. - כיוון שאנו מנחשים שזה פתרון של המד"ר, נציב אותו בתוך המשוואה ונמצא (בתקווה) פונקציה
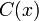 כך שהמשוואה תתקיים.
כך שהמשוואה תתקיים.
- כלומר, נציב
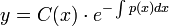 במשוואה
במשוואה 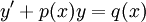 .
. - נקבל
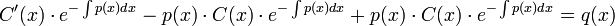
- משוואה זו מתקיימת אם"ם
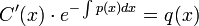 .
. - כלומר
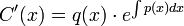 .
. - לכן נבחר
![C(x)=\int \left[q(x)\cdot e^{\int p(x)dx}\right]dx+C](/images/math/6/c/f/6cf87e99cd8a2a5177febbf421fd76f7.png)
- סה"כ הפתרון הכללי למד"ר הלינארית
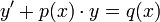 הוא:
הוא:
- דוגמא - המשוואה החביבה עלינו
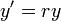 :
:
- ראשית, נשים לב כי
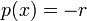 ו
ו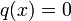 .
. - כלומר זו מד"ר לינארית הומוגנית, והפתרון הכללי הוא
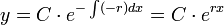
- ראשית, נשים לב כי
נפילה חופשית כולל התנגדות אוויר
- גוף בעל מסה
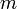 נמצא בנפילה חופשית, מצד אחד הוא מושפע מכוח הכבידה שנחשב קבוע
נמצא בנפילה חופשית, מצד אחד הוא מושפע מכוח הכבידה שנחשב קבוע 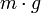 ומצד שני מכוח התנגדות האוויר.
ומצד שני מכוח התנגדות האוויר. - במהירויות גבוהות נניח שהוא פרופורציונלי למהירות הנפילה בריבוע
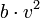 , ובמהירויות נמוכות נניח שהוא פרופורציונלי למהירות הנפילה
, ובמהירויות נמוכות נניח שהוא פרופורציונלי למהירות הנפילה 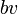 .
.
במהירות גבוהה
- לפי החוק השני של ניוטון
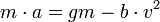 .
. - כלומר
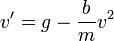
- נבצע הפרדת משתנים
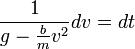
- נבצע פירוק לשברים חלקיים:
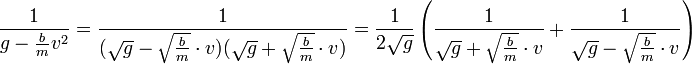
- ולכן

- מצד שני
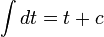
- לכן
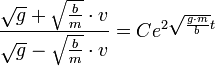
- נסדר קצת
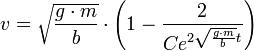
- נשים לב שכאשר
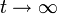 אנו מתכנסים למהירות הסופית
אנו מתכנסים למהירות הסופית 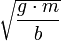 .
. - אם זו הייתה המהירות ההתחלתית היינו מקבלים פונקצית מהירות קבועה.
במהירות נמוכה
- לפי החוק השני של ניוטון
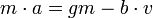 .
. - כלומר קיבלנו את המד"ר הלינארית
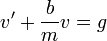 .
. - ולכן הפתרון הוא
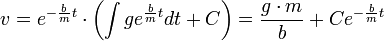 .
. - וכאשר
 המהירות שואפת למהירות הסופית
המהירות שואפת למהירות הסופית 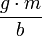 .
.
משוואת ברנולי
- משוואת ברנולי היא משוואה מהצורה
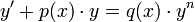 עבור
עבור 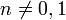 .
. - נפתור את המשוואה על ידי הצבה שתהפוך אותה למשוואה לינארית, אותה כבר למדנו לפתור.
- נניח כי
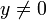 , ונחלק ב
, ונחלק ב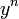 .
. - נקבל את המשוואה
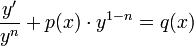 .
. - נציב
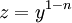 .
. - נגזור
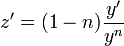 .
. - נקבל משוואה לינארית
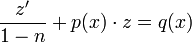 .
. - נפתור עבור
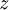 ונציב חזרה לקבל
ונציב חזרה לקבל 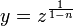 .
.
- דוגמא - נפתור את המשוואה
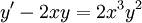 .
.
- נציב
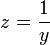 .
. - נקבל
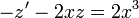 ולכן
ולכן 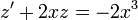 .
. - לכן
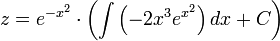
- לכן
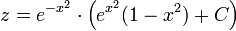
- לכן
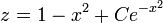
- ולבסוף
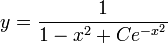
- נציב
- דוגמא - גוף בתנועה עם כוח גרר לא לינארי ביחס למהירות
- נתון גוף הנע חצי באוויר וחצי בתוך נוזל כלשהו. נניח כי החיכוך עם הנוזל פרופורציונלי למהירות, והחיכוך עם האוויר פרופורציונלי למהירות בריבוע.
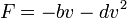 ולכן
ולכן 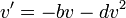 (לצורך הפשטות הכנסנו את המסה לתוך הקבועים).
(לצורך הפשטות הכנסנו את המסה לתוך הקבועים).- זוהי משוואת ברנולי, נציב
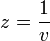 .
. - לכן
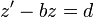
- נפתור את המשוואה הדיפרנציאלית:
- ולכן
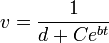
- כמובן שכאשר
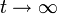 המהירות מתכנסת מהר מאד לאפס.
המהירות מתכנסת מהר מאד לאפס.
הרצאה 3 משוואות מדוייקות ומשפט הקיום והיחידות
הקדמה - פונקציות בשני משתנים
- נגזרות חלקיות
- דוגמא עבור
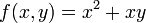 מתקיים
מתקיים 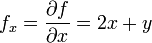 ו
ו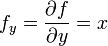
- דוגמא עבור
- עבור פונקציות דיפרנציאביליות (כמו הפונקציות האלמנטריות), מתקיים כי
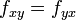 (כלומר סדר הנגזרות לא משנה).
(כלומר סדר הנגזרות לא משנה). - כלל השרשרת: אם
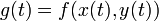 אזי
אזי 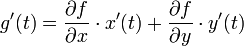
- בפרט, עבור
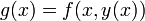 מתקיים
מתקיים 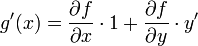
מד"ר מדוייקת
- מד"ר נקראת מדוייקת אם היא מהצורה
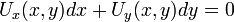 , עבור
, עבור 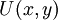 דיפרנציאבילית.
דיפרנציאבילית. - פתרון המד"ר ניתן בצורה סתומה על ידי המשוואה
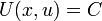 , כאשר C קבוע כלשהו.
, כאשר C קבוע כלשהו. - מד"ר מהצורה
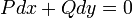 היא מדוייקת אם"ם
היא מדוייקת אם"ם 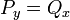 ו
ו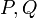 בעלות נגזרות רציפות.
בעלות נגזרות רציפות.
- הוכחה לפתרון המד"ר המדויקת:
- נגזור את הפונקציה
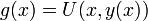 לפי המשתנה
לפי המשתנה 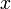 באמצעות כלל השרשרת ונקבל כי
באמצעות כלל השרשרת ונקבל כי 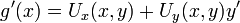
- לפי הנתון
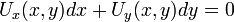 נובע כי
נובע כי 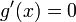 ולכן
ולכן 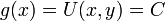 פונקציה קבועה.
פונקציה קבועה.
- נגזור את הפונקציה
- הוכחה לתנאי השקול למד"ר מדויקת:
- כיוון ראשון, נניח
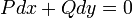 מדוייקת.
מדוייקת.
- לכן קיימת
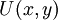 דיפרנציאבילית כך ש
דיפרנציאבילית כך ש 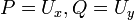 .
. - לכן
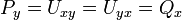 .
.
- לכן קיימת
- כיוון שני, נניח כי
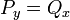 .
.
- אנו מחפשים
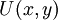 עבורה
עבורה 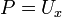 .
. - נעשה אינטגרציה לפי
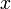 ונקבל כי
ונקבל כי 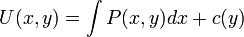 .
. - לכן ברור כי
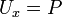 , השאלה היא אם ניתן לבחור
, השאלה היא אם ניתן לבחור 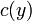 עבורו
עבורו 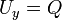 .
. - כלומר אנו רוצים
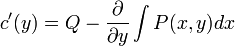
- משוואה זו תהיה פתירה, אם הצד הימני הוא פונקציה שאינה תלוייה בx.
- אכן
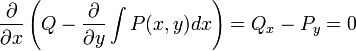 .
.
- אנו מחפשים
- כיוון ראשון, נניח
- דוגמא: נפתור את המשוואה
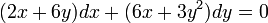 .
. - ראשית נוודא שמדובר במשוואה מדוייקת:
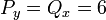 .
. - נבצע אינטגרציה
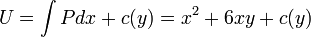 .
. - נגזור לפי y ונקבל כי
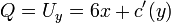 .
. - לכן
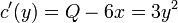 .
. - לכן
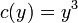 וסה"כ
וסה"כ 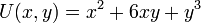 .
. - לכן הפתרון למד"ר הוא
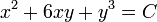 .
.