שיחה:88-132 סמסטר א' תשעא

חזרה לדף הקורס

גלול לתחתית העמוד

הוספת שאלה חדשה

הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).

-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן

אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.

ארכיון

• ארכיון 1
• ארכיון 2
• ארכיון 3
• ארכיון 4
• ארכיון 5
• ארכיון 6
• ארכיון 7
• ארכיון 8
• ארכיון 9

שאלות

תרגול עם אפי

מישהו יודע איפה התירגול מחר בבוקר עם אפי כהן?

מבנה 216, חדר 201.

לגבי הבוחן.

צריך לדעת לבוחן את התהליך וביצועו של שינוי איברים בטור בכדי שיתכנס? או שמספיק לדעת לבוחן אם ניתן לעשות את השינוי/ מתכנסת בהחלט וכו... [ידוע שצריך לדעת את החומר הזה בגדול והן למבחן הסופי, השאלה אם זה גם נכלל בהיקף המידע והביצוע של הבוחן....] תודה.

לא צריך את זה לבוחן. --ארז שיינר 20:43, 5 בדצמבר 2010 (IST)

הגשת תרגיל 8

אם אפשר לדעת מתי תאריך הגשת תרגיל 8

תלוי מי. אצלי (ארז) ההגשה היא לשבוע הקרוב, כלומר יום ראשון --ארז שיינר 20:18, 6 בדצמבר 2010 (IST)

אם אתה אצל אפי, ההגשה גם ביום א (הבהרה: הודעה זו נשלחה על ידי תלמיד של אפי ולא על ידי אפי עצמו...)

ומי שאצל אדוארד?

בוחן

שלום רב,

האם תעלו בהמשך את הבוחן ואת התשובות לו (אני מדבר גם על הוחן שנערך לתיכוניסטים וגם לבוחן שנערך לסטודנטים הרגילים)?

תודה רבה מראש!

לגבי התיכוניסטים אני לא יודע, לרגילים נעלה בימים הקרובים

תרגיל 7 שאלה 3

ארז, לא הבנתי את הפתרון שלך לשאלה 3 בתרגיל 7 (הבנתי את מה שאמרת בהתחלה, ואז כשפירקת את הסכום ל2 שברים, לא הבנתי בכלל מאיפה הגעת אליהם). אפשר קצת הסבר? תודה!

תשובה

תציב שם a=0,1,...5 ותראה שסה"כ מקבלים את כל האינדקסים האפשריים. למה הדבר דומה? נסתכל על מספרים קטנים יותר, במקום 12 ניקח 4. נראה לחלק את הטוב 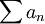$\sum a_n$ לשני טורים: 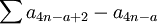$\sum a_{4n-a+2}-a_{4n-a}$ עבור a=0,1.

מה נקבל? 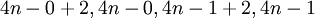$4n-0+2,4n-0,4n-1+2,4n-1$ שזה סה"כ 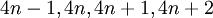$4n-1,4n,4n+1,4n+2$ וזה בדיוק לחלק את הסדרה ל4 תתי סדרות שבהן לוקחים כל איבר רביעי..

אחרי שמבינים שלקחנו 12 תתי סדרות, שאר הפתרון הוא אלגברי/טריגונומטרי/אינפיניטיסימלי :) --ארז שיינר 18:36, 8 בדצמבר 2010 (IST)

אבל לא הבנתי גם את הרעיון שמאחורי ההוכחה.. הרי חילוק לתתי סדרות הוא כמו השמת סוגריים (נראה לי), ולמדנו שאם הטור שהתקבל מטור אחר ע"י השמת סוגריים והטור המקורי לא מתכנסים ומתבדרים יחד..

זה לא כמו השמת סוגריים, בכיתה שלי הראתי כיצד אפשר לחלק טורים באופן חוקי. נניח אתה רוצה לחלק טור לשניים, אתה פשוט מאפס פעם את האיברים הזוגיים ופעם את האי זוגיים. בינתיים ברור שסכום שני הטורים הללו שווה למקורי. עכשיו יש משפט שאם אתה מעלים את האפסים האלה, סכום הטור נשאר זהה. והנה חלקנו טור לסכום טור האיבריים הזוגיים וטור האיברים האי זוגיים. (בתרגיל אנחנו מחלקים ל6 טורים בעלי סימנים מתחלפים). --ארז שיינר 13:18, 10 בדצמבר 2010 (IST)

אה, הבנתי, אבל לא עשינו את זה בכיתת התרגול שלי (אדוארד)...

אפשר להראות את זה גם בעזרת סכומים חלקיים. כל סכום חלקי של הטור ניתן לפרק לסכום של שישה סכומים חלקיים אחרים, כאשר אלה מתכנסים, ואז להשתמש באריתמטיקה של גבולות של סדרות. --ארז שיינר 13:46, 10 בדצמבר 2010 (IST)

לא הבנתי את שאלה 7 (תרגיל 7)..

איך בסעיף א' זה מתבדר וב-ב' זה מתכנס?? שני התנאים בסעיפים א' ו-ב' הם אותו התנאי!!

התנאי איננו אותו התנאי בשני הסעיפים, התנאי בסעיף ב' חזק יותר. בסעיף ב' לא רק שהמנה בערך מוחלט קטנה מ1, אלא גם קיים איזשהו מספר קטן מ1 שהמנה בערך מוחלט תהיה תמיד קטנה שווה לו, כלומר היא לא שואפת ל1, מה שיכול להיות בסעיף א'. לראיה קח את הסדרה 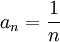${a_n} = \frac{1}{n}$, המקיימת את התנאי שבסעיף א' ואינה מקיימת את התנאי שבסעיף ב'. -לידור.א.- 12:20, 10 בדצמבר 2010 (IST)

אבל התנאי בסעיף א' גורר את ב', כי אם נסמן את הביטוי הזה שקטן מאלפא xn, אז נניח בשלילה שxn<1 לכל n אבל לא מתקיים ש xn<=a<1 לכל n, ולכן קיים n שבשבילו xn>a, לכל a שקטן מאחד, או במילים אחרות xn הוא חסם מלעיל של הקבוצה 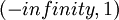$(-infinity, 1)$ ולכן xn הנ"ל בהכרח גדול שווה ל1 בסתירה לכך שהוא קטן מאחד. לא ככה?

תנאי ב' גורר את תנאי א'. אתה ניסית להוכיח ההפך, אבל בחוסר הצלחה. x_n אינו מספר מסויים שגדול מכל a. זו סדרה שיש בה איברים שגדולים מכל a. דוגמא פשוטה: 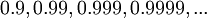$0.9,0.99,0.999,0.9999,...$. ברור שאין a קטן מאחד שגדול יותר מכל איברי הסדרה כיוון שהיא שואפת לאחד. --ארז שיינר 13:20, 10 בדצמבר 2010 (IST)

לא הבנתי...... x_n עבור n מסוים הוא מספר, לא סדרה...

רשמת "ולכן קיים n שבשבילו xn>a, לכל a שקטן מאחד" זה לא נכון. לכל a יהיה x_n אחר כמו בדוגמא לעיל, כמו בחסמים.--ארז שיינר 13:20, 10 בדצמבר 2010 (IST)

עכשיו אני מבין בערך את הכוונה של מה שאתם אומרים, אבל זה עדיין לא מסתדר עם העובדה, שהשלילה של המשפט, "לכל n מתקיים x_n (הביטויים התהפכו) קטן מכל a שקטן מאחד" (המשפט הנתון), היא "קיים x_n שגדול מכל a שקטן מאחד".

לא נסחת את המשפט כמו שצריך ולכן השלילה שגוייה. המשפט הינו "קיים a כך שלכל n מתקיים x_n<a", והשלילה שלו הינה "לכל a קיים n כך ש x_n>=a" --ארז שיינר 13:49, 10 בדצמבר 2010 (IST)

משפט ליפשיץ ומשפט לייבניץ

בתרגול, כתבנו שמשפט לייבניץ, הוא מה שכתבנו בהרצאה שהוא משפט ליפשיץ. (על התכנסות טור מתחלף). מישהו שיודע בוודאות, יכול להגיד מהו משפט ליפשיץ ומהו משפט לייבניץ? תודה!

משפט לייבניץ - תהי an סדרה לא עולה חיובית מתכנסת לאפס, אזי הטור 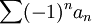$\sum (-1)^na_n$מתכנס.

אז מה זה משפט ליפשיץ?

לא יודע.