מתמטיקה בדידה - ארז שיינר
מתוך Math-Wiki
תוכן עניינים
חומר עזר
סרטוני ותקציר הרצאות
פרק 1 - מבוא ללוגיקה מתמטית
פסוקים, קשרים, כמתים, פרדיקטים
תרגול
אינדוקציה
תרגול
פרק 2 - מבוא לתורת הקבוצות
קבוצות ופעולות על קבוצות
שיטות הוכחה בסיסיות
איחוד וחיתוך כלליים
קבוצת החזקה
תרגול
פרק 3 - יחסים
מכפלה קרטזית ויחסים
יחסי שקילות
תרגול
יחסי סדר
איברים מינימליים ומקסימליים, וחסמים
תרגול
פרק 4 - פונקציות
הגדרת פונקציות
חח"ע ועל, תמונה ותמונה הפוכה
הרכבת פונקציות, פונקציות הפיכות
פונקציה מוגדרת היטב
תרגול
פרק 5 - עוצמות
מבוא
השוואת עוצמות
משפט קנטור
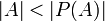
משפט קנטור-שרדר-שרנשטיין
- אם
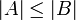 וגם
וגם 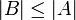 אזי
אזי 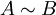
למת נקודת השבת
- תהי פונקציה עולה
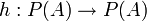 כלומר המקיימת לכל
כלומר המקיימת לכל 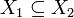 כי
כי 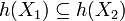
- אזי קיימת נק' שבת
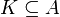 כך ש
כך ש 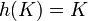 .
.
הוכחת המשפט
נושאים שעוד לא נערכו
- משפט ק.ש.ב
- משפט קנטור
- קבוצות בנות מנייה, עוצמת תתי קבוצות של הטבעיים.
- עקרון המקסימום של האוסדורף
- אקסיומת הבחירה
- קשר בין פונקציה על להשוואת עוצמות
- כל קבוצה אינסופית גדולה שווה מאלף אפס
- אריתמטיקה של עוצמות
- סכום עוצמות
- כפל עוצמות
- חזקת עוצמות
- הקשר בין השוואת הקבוצות לפני הפעולה, להשוואתן אחרי הפעולה
- הקשר בין אלף אפס לאלף
- סכום וכפל עוצמות הוא המקסימום
- תמיד ניתן להשוות עוצמות