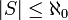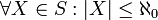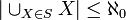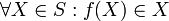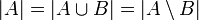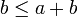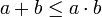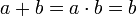מתמטיקה בדידה - ארז שיינר
מתוך Math-Wiki
תוכן עניינים
- 1 חומר עזר
- 2 סרטוני ותקציר הרצאות
- 2.1 פרק 1 - מבוא ללוגיקה מתמטית
- 2.2 פרק 2 - מבוא לתורת הקבוצות
- 2.3 פרק 3 - יחסים
- 2.4 פרק 4 - פונקציות
- 2.5 פרק 5 - עוצמות
- 2.5.1 מבוא
- 2.5.2 השוואת עוצמות
- 2.5.3 משפט קנטור
- 2.5.4 קבוצות בנות מנייה
- 2.5.5 חשבון עוצמות (אריתמטיקה של עוצמות)
- 2.5.6 משפט קנטור-שרדר-ברנשטיין
- 2.5.7 איחוד בן מנייה של קבוצות בנות מנייה
- 2.5.8 אקסיומת הבחירה ועקרון המקסימום של האוסדורף
- 2.5.9 השוואת עוצמות
- 2.5.10 סכום ומכפלה של עוצמות אינסופיות שווה לגדולה מבין העוצמות
- 2.5.11 הקשר בין עוצמת הטבעיים לעוצמת הממשיים
- 2.5.12 תרגול
חומר עזר
סרטוני ותקציר הרצאות
פרק 1 - מבוא ללוגיקה מתמטית
פסוקים, קשרים, כמתים, פרדיקטים
תרגול
אינדוקציה
תרגול
פרק 2 - מבוא לתורת הקבוצות
קבוצות ופעולות על קבוצות
- איבר שייך לקבוצה
 אם הוא אחד האיברים בקבוצה.
אם הוא אחד האיברים בקבוצה. - קבוצה מוכלת בקבוצה אחרת
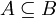 אם
אם 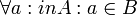
- תהי קבוצה
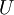 ותהיינה
ותהיינה 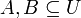 . נגדיר את:
. נגדיר את:
- קבוצת האיחוד
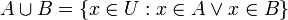
- קבוצת החיתוך
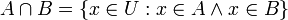
- קבוצת ההפרש
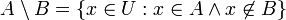
- קבוצת המשלים
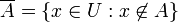
- קבוצת האיחוד
שיטות הוכחה בסיסיות
איחוד וחיתוך כלליים
- תהי S קבוצה של קבוצות, נגדיר:
קבוצת החזקה
תרגול
פרק 3 - יחסים
מכפלה קרטזית ויחסים
תכונות של יחסים
- יהי R יחס על A (כלומר
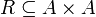 ) אזי:
) אזי:
- R נקרא רפקסיבי אם לכל
 מתקיים
מתקיים 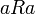 .
. - R נקרא סימטרי אם לכל
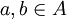 המקיימים
המקיימים 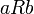 מתקיים
מתקיים 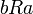
- R נקרא אנטי-סימטרי אם לכל
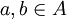 המקיימים
המקיימים 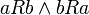 מתקיים
מתקיים 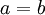
- R נקרא רפלקסיבי אם לכל
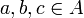 המקיימים
המקיימים 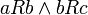 מתקיים
מתקיים 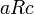
- R נקרא מלא אם לכל
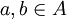 מתקיים כי
מתקיים כי 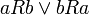
- R נקרא רפקסיבי אם לכל
- יהי R יחס מA לB (כלומר
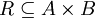 ) אזי:
) אזי:
- R נקרא חד-ערכי (ח"ע) אם לכל
 ולכל
ולכל 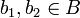 המקיימים
המקיימים 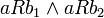 מתקיים
מתקיים 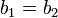
- R נקרא שלם אם לכל
 קיים
קיים 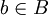 כך ש
כך ש 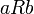
- R נקרא חד-חד-ערכי (חח"ע) אם לכל
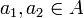 ולכל
ולכל 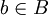 המקיימים
המקיימים 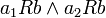 מתקיים
מתקיים 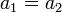
- R נקרא על אם לכל
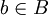 קיים
קיים  כך ש
כך ש 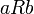
- R נקרא חד-ערכי (ח"ע) אם לכל
יחסי שקילות
תרגול
יחסי סדר
איברים מינימליים ומקסימליים, וחסמים
תרגול
פרק 4 - פונקציות
הגדרת פונקציות
חח"ע ועל, תמונה ותמונה הפוכה
הרכבת פונקציות, פונקציות הפיכות
פונקציה מוגדרת היטב
תרגול
פרק 5 - עוצמות
מבוא
השוואת עוצמות
- A שקולת עוצמה לB או עוצמתה של A שווה לB, אם קיימת פונקציה הפיכה (חח"ע ועל)
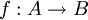 .
. - במקרה זה מסמנים
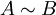 או
או 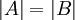 .
.
- כל קבוצה שקולת עוצמה לעצמה
- אם A שקולת עוצמה לB, גם B שקולת עוצמה לA
- אם A שקולת עוצמה לB וB שקולת עוצמה לC אזי A שקולת עוצמה לC
- עוצמתה של A קטנה או שווה לזו של B, אם קיימת פונקציה חח"ע
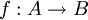 .
. - במקרה זה מסמנים
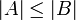
- כל קבוצה A השקולת עוצמה לקבוצת הטבעיים מסומנת
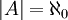
- כל קבוצה A השקולת עוצמה לקבוצת הממשיים מסומנת
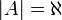
משפט קנטור
קבוצות בנות מנייה
- קבוצה A נקראת בת מנייה אם
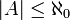
- כל קבוצה A בת מנייה אינסופית מקיימת
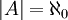
חשבון עוצמות (אריתמטיקה של עוצמות)
חיבור עוצמות
- תהיינה שתי עוצמות a,b ותהיינה שתי נציגות זרות לעוצמות A,B.
- נגדיר
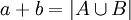 , הגדרה זו אינה תלוייה בבחירת הנציגות.
, הגדרה זו אינה תלוייה בבחירת הנציגות.
כפל עוצמות
- תהיינה שתי עוצמות a,b ותהיינה שתי נציגות לעוצמות A,B.
- נגדיר
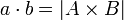 , הגדרה זו אינה תלוייה בבחירת הנציגות.
, הגדרה זו אינה תלוייה בבחירת הנציגות.
חזקת עוצמות
- תהיינה שתי עוצמות a,b ותהיינה שתי נציגות לעוצמות A,B.
- נגדיר את
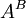 להיות אוסף כל הפונקציות מB לA (מהמעריך לבסיס).
להיות אוסף כל הפונקציות מB לA (מהמעריך לבסיס). - נגדיר
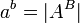 , הגדרה זו אינה תלוייה בבחירת הנציגות.
, הגדרה זו אינה תלוייה בבחירת הנציגות.
- חוקי חזקות
- תהיינה עוצמות a,b,c אזי
עוצמת קבוצת החזקה
השוואת חשבון עוצמות
- תהיינה עוצמות a,b,c,d כך ש
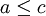 וכן
וכן 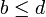 אזי:
אזי:
- אם בנוסף נתון כי
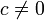 אזי
אזי
משפט קנטור-שרדר-ברנשטיין
- אם
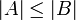 וגם
וגם 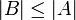 אזי
אזי 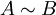
למת נקודת השבת
- תהי פונקציה עולה
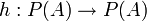 כלומר המקיימת לכל
כלומר המקיימת לכל 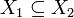 כי
כי 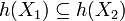
- אזי קיימת נק' שבת
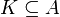 כך ש
כך ש 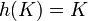 .
.
הוכחת המשפט
עוצמות קטעים ממשיים
איחוד בן מנייה של קבוצות בנות מנייה
- תהי S קבוצה בת מנייה של קבוצות בנות מנייה, כלומר:
- אזי גם האיחוד הכללי הוא בן מנייה:
- מסקנה: אוסף תתי הקבוצות הסופיות של המספרים הטבעיים הוא בן מנייה.
אקסיומת הבחירה ועקרון המקסימום של האוסדורף
אקסיומת הבחירה
- תהי S קבוצת קבוצת לא ריקות, ונסמן את האיחוד הכללי ב
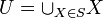 .
. - אזי קיימת פונקצית בחירה
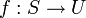 הבוחרת איבר מתוך כל קבוצה, כלומר:
הבוחרת איבר מתוך כל קבוצה, כלומר:
- דוגמא:
- תהי פונקציה על
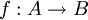 אזי קיימת תת קבוצה
אזי קיימת תת קבוצה 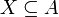 כך ש
כך ש 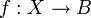 חח"ע ועל.
חח"ע ועל.
- תהי פונקציה על
- תהיינה
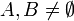 אזי
אזי 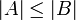 אם ורק אם קיימת
אם ורק אם קיימת 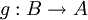 על.
על.
עקרון המקסימום של האוסדורף
- תהי קבוצה A עם יחס סדר חלקי, תת קבוצה
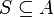 נקראת שרשרת אם היחס מלא עליה (ניתן להשוות בין כל שני איברים בS).
נקראת שרשרת אם היחס מלא עליה (ניתן להשוות בין כל שני איברים בS). - שרשרת נקראת מקסימלית בA אם היא אינה מוכלת באף שרשרת אחרת.
- עקרון המקסימום של האוסדורף אומר שכל שרשרת מוכלת בשרשרת מקסימלית.
- דוגמא - אוסף עיגולים במישור שאינם חותכים זה את זה, ולא ניתן להוסיף אפילו עיגול אחד נוסף.
אלף אפס היא העוצמה האינסופית הקטנה ביותר
(בהנחת עקרון המקסימום של האוסדורף)
- תהי A קבוצה אינסופית, אזי
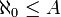
- תהי A קבוצה אינסופית, ותהי B קבוצה סופית, אזי:
השוואת עוצמות
(בהנחת עיקרון המקסימום של האוסדורף)
- תהיינה שתי קבוצות A,B אזי
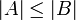 או
או 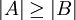
סכום ומכפלה של עוצמות אינסופיות שווה לגדולה מבין העוצמות
- תהיינה עוצמות
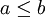 אזי:
אזי:
- נניח בנוסף כי
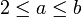 אזי:
אזי:
- נניח בנוסף כי b אינסופית, ונקבל ביחד
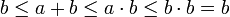 (המעבר
(המעבר 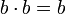 מוכח בסרטון השני).
מוכח בסרטון השני).
- ולכן לפי משפט ק.ש.ב נקבל כי
- תהי עוצמה אינסופית b אזי
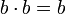
הקשר בין עוצמת הטבעיים לעוצמת הממשיים
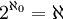 כלומר
כלומר 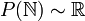
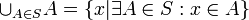
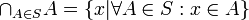
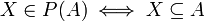
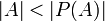
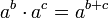
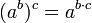
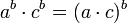
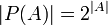
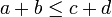
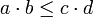
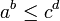
![|\mathbb{R}|=|[a,\infty)|=|[a,b]|=|(a,b)|=\aleph](/images/math/e/2/8/e28f470d9989f90392ac879da050605e.png)