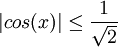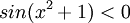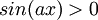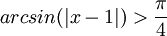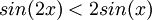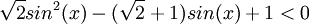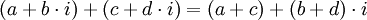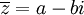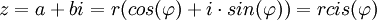מכינה למחלקת מתמטיקה/מערכי שיעור/4
פונקציות טריגונומטריות הופכיות
ניתן להגדיר פונקציה הופכית רק כאשר לכל איבר בתמונה קיים מקור יחיד. לכל פונקציה טריגונומטרית נבחר את התחום המתאים.
תרגיל: הוכח כי 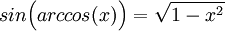
תרגילים
מצא לאילו ערכי x מתקיימים אי השיוויונים הבאים:
מספרים מרוכבים
נביט באוסף האיברים מהצורה
כאשר 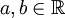 והאות i הינה לצורך סימון בלבד. נקרא לאוסף זה מספרים מרוכבים.
והאות i הינה לצורך סימון בלבד. נקרא לאוסף זה מספרים מרוכבים.
נגדיר פעולות חיבור וכפל בין מספרים מרוכבים:
שימו לב כי 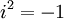
בנוסף לכל מספר מרוכב 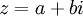 נגדיר את הצמוד המרוכב:
נגדיר את הצמוד המרוכב:
תרגיל חשב את 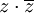
פתרון 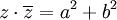
- הערה: נסמן
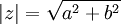
- הערה: נסמן
תרגיל הוכח שלכל מספר מרוכב 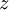 קיים מספר מרוכב
קיים מספר מרוכב 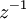 כך ש
כך ש 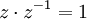 .
.
פתרון: 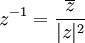
- הערה: באופן כללי נסמן
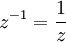
- הערה: באופן כללי נסמן
תרגיל חשב את הביטוי 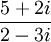
הגדרה: עבור מספר מרוכב 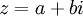
- החלק הממשי
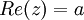
- החלק הממשי
- החלק המדומה
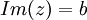
- החלק המדומה
לדוגמא:
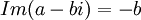
תרגיל: הוכח כי 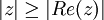
תרגיל: הוכח את אי-שיוויון המשולש 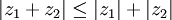
המישור המרוכב
כל מספר מרוכב 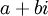 מתאים לנקודה
מתאים לנקודה 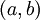 במישור המרוכב.
במישור המרוכב.
ניתן לתאר את המספר המרוכב באופן יחיד באמצעות המרחק מראשית הצירים וזוית כלפי ציר האיקס.
מתקיים:
- אם
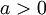 אזי
אזי 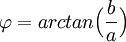
- אם
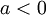 אזי
אזי 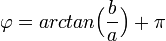
- אם
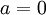 וגם
וגם 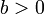 אזי
אזי 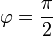
- אם
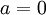 וגם
וגם 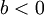 אזי
אזי 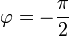
- אם
הצורה 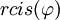 נקראת הצורה הפולארית של המספר המרוכב, ואילו
נקראת הצורה הפולארית של המספר המרוכב, ואילו 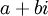 היא הצורה הקרטזית.
היא הצורה הקרטזית.
![arcsin(x):[-1,1]\rightarrow [-\frac{\pi}{2},\frac{\pi}{2}]](/images/math/a/d/8/ad87e9d8d48f94ca443b202a6ac1c6d9.png)
![arccos(x):[-1,1]\rightarrow [0,\pi]](/images/math/4/4/5/445e4a4ac23bf5bc584557717c908d37.png)
![arctan(x):(-\infty,\infty)\rightarrow [-\frac{\pi}{2},\frac{\pi}{2}]](/images/math/d/0/0/d000c19ff4d1baafa10401c931e511b8.png)