שיחה:88-132 סמסטר א' תשעא
תוכן עניינים
הוספת שאלה חדשה
הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).
-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן
אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.
ארכיון
שאלות
תרגיל 8 שאלות 6 ו-2
ב-6: למה הכוונה כשאומרים שהפונקציה חסומה בקטע? זאת אומרת שהפונקציה חסומה ע"י מספר כלשהו? (לא נראה לי שלמדנו את ההגדרה לכך) ב-2: אני הבנתי את הראציונאל אבל אני כבר שעה יושב על התרגיל ולא מצליח להגיע לביטוי שגדול מ-הדרוש אך רק תלוי דלתא... אפשר רמז?
שלילת הגבול של פונקציה
אפשר את ההגדרה של שלילת גבול של פונקציה תודה
תשובה
שלילת הגבול לפי קושי:
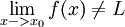 אם קיים
אם קיים 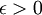 כך שלכל
כך שלכל 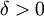 קיים x כך ש
קיים x כך ש 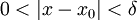 עבורו מתקיים
עבורו מתקיים 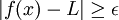
שלילות הגבול לפי היינה:
1. 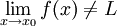 אם קיימת סדרה
אם קיימת סדרה 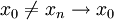 כך ש
כך ש 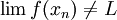 .
.
2. אם קיימות שתי סדרות 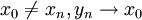 כך שמתקיים
כך שמתקיים 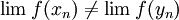 אזי אין גבול לf בנקודה x_0
אזי אין גבול לf בנקודה x_0
3. אם קיימת סדרה 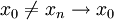 כך ש
כך ש 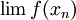 לא קיים, אזי אין גבול לf בנקודה x_0
לא קיים, אזי אין גבול לf בנקודה x_0
תרגיל 8, שאלה 3.
לא הבנתי איך אמורים להוכיח בעזרת היינה את הגבול של הפונקציה הנתונה, הרי המרצה גם אמר לנו במפורש שאי אפשר להוכיח גבולות בעזרת היינה, מכיוון שאי אפשר להוכיח משהו על כל הסדרות בעולם, ושתמיד צריך להוכיח אם קושי. ? אם אי אפשר להוכיח על כל הסדרות בעולם אז אי אפשר להוכיח לפי היינה.... אבל בשאלה הזאת אתה כן מוכיח לכל הסדרות בעולם... (שמתכנסות לאפס מין הסתם)
תשובה
אפשר להוכיח דברים על כל הסדרות בעולם שמתכנסות לאפס, יש לנו משפטים כאלה. זה לא שאי אפשר אלא שבדר"כ זה קשה יותר. כאן זה לא... --ארז שיינר 01:27, 17 בדצמבר 2010 (IST)
- הצלחתי- והאמת שבקלות! תודה רבה!
תרגול 9, שאלה 3
הגבול של  הוא ממשי או שגם יכול להיות אינסוף? תודה, גל.
הוא ממשי או שגם יכול להיות אינסוף? תודה, גל.
- ממשי --ארז שיינר 01:29, 17 בדצמבר 2010 (IST)
תרגיל 9 שאלה 5
האם נכון להוכיח באופן הבא? נסמן את הפונקציה F ב Y ואז הגבול של G כאשר X שואף לX אפס שווה לגבול של G של Y כאשר Y שואף לA . וז מכיון ש G רציפה ב A גבולה בA שווה לערכה בA
- לא, זו לא הוכחה, זה מה שצריך להוכיח. צריך באמצעות אפסילון ודלתא... --ארז שיינר 23:47, 17 בדצמבר 2010 (IST)
- הוכחתי באמצעות היינה, האם זה יתקבל?
שאלה, האם מותר להשתמש בזהות בטריגונומטרית
מותר להשתמש בזהות הטריגונומטרית שעבור זויות  קטנות
קטנות 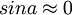 ?
(שמדובר בקטנות הכוונה היא ששואפים ל-0)
תודה, שקד רטר 21:58, 17 בדצמבר 2010 (IST)
?
(שמדובר בקטנות הכוונה היא ששואפים ל-0)
תודה, שקד רטר 21:58, 17 בדצמבר 2010 (IST)
- לא יודע מה אומר הסימון הזה. אפשר להשתמש בכך ש
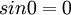 כמובן, וכמו כן מותר להשתמש בעובדה ש
כמובן, וכמו כן מותר להשתמש בעובדה ש 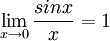 וגם
וגם 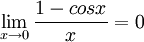 --ארז שיינר 00:36, 18 בדצמבר 2010 (IST)
--ארז שיינר 00:36, 18 בדצמבר 2010 (IST)
- התבלבלתי בכתיבה התכוונתי ש-
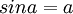 , והסימון מתכוון שכמעט מתקיים שוויון
, והסימון מתכוון שכמעט מתקיים שוויון
- מה זה כמעט שיוויון? אני מניח שאתה מתכוון לגבול המצויין לעיל. --ארז שיינר 12:38, 18 בדצמבר 2010 (IST)
- אני מתכוון ש< math>sina</math> שואף ל-0 וגם
 שואף ל-0 אז אפשר להגיד ש-
שואף ל-0 אז אפשר להגיד ש- 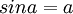 ? סליחה אם לא הייתי מובן זה פשוט תכונה שלמדתי בפיזיקה פעם,השאלה היא פשוט האם מותר להיעזר בזה...תודה
? סליחה אם לא הייתי מובן זה פשוט תכונה שלמדתי בפיזיקה פעם,השאלה היא פשוט האם מותר להיעזר בזה...תודה
- אני מתכוון ש< math>sina</math> שואף ל-0 וגם
- מה זה כמעט שיוויון? אני מניח שאתה מתכוון לגבול המצויין לעיל. --ארז שיינר 12:38, 18 בדצמבר 2010 (IST)
- התבלבלתי בכתיבה התכוונתי ש-
תרגיל 9 - שאלה 4א'
שלום,
רציתי לדעת אם הדרך שלי היא נכונה.
אני רוצה להוכיח שהגבולות החד צדדיים של  שווים ושווים ל-0 וביחד עם הנתון ש-f רציפה ב-0 לקבוע ש
שווים ושווים ל-0 וביחד עם הנתון ש-f רציפה ב-0 לקבוע ש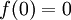 .
בעיקרון אני אומר ככה:
.
בעיקרון אני אומר ככה:
1) לכל 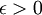 קיים
קיים 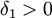 כך שאם
כך שאם 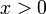 ומתקיים
ומתקיים 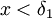 אז מתקיים
אז מתקיים 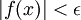
2) לכל 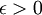 קיים
קיים 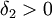 כך שאם
כך שאם 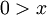 ומתקיים
ומתקיים 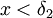 אז מתקיים
אז מתקיים 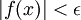
נקח 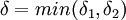 ולכן
לפי הנתון ש-
ולכן
לפי הנתון ש-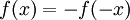 אם
אם 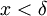 וזה גורר ש
וזה גורר ש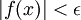 ולכן
ולכן
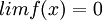 ומכיוון ש-
ומכיוון ש- רציפה ב-x=0 אזי
רציפה ב-x=0 אזי 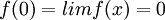
האם זה בסדר?
- (לא מתרגל) אני מניח שהתבלבלת בכתיבת טענותיך, שכן חלק מהתנאים שלך לא הגיוניים. לדוגמה בטענה השנייה שלך כתבת "קיים
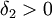 כך שאם
כך שאם 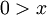 ומתקיים
ומתקיים 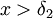 ", דבר שהוא בלתי אפשרי שכן x לא יכול להיות גם קטן מ0 וגם גדול מדלתא 2 שגדול מ0. -לידור.א.- 15:27, 18 בדצמבר 2010 (IST)
", דבר שהוא בלתי אפשרי שכן x לא יכול להיות גם קטן מ0 וגם גדול מדלתא 2 שגדול מ0. -לידור.א.- 15:27, 18 בדצמבר 2010 (IST)
- נכון, טעיתי בכתיבת הטענות ועכשיו תיקנתי. אשמח אם תוכל שוב לבחון את המקרה לאחר תיקון הטעויות. תודה רבה
- אני לא מבין מאיפה הגיעו טענות 1 ו2, הן לא נובעות ישירות מהנתון. כמו כן, בטענה 2 הייתי מצפה לראות
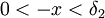 ולא
ולא 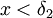 כי זה חסר משמעות למספר שלילי --ארז שיינר 16:22, 18 בדצמבר 2010 (IST)
כי זה חסר משמעות למספר שלילי --ארז שיינר 16:22, 18 בדצמבר 2010 (IST)
- בטענה 2 הגדרתי את X להיות קטן מאפס אבל אפשר שX יהיה גדול מאפס ואז באמת
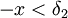 .
.
טענות 1,2 הם עבור הגבולות החד צדדיים. אני מנסה להראות שהגבולות החד צדדיים קיימים ושווים ל-0. הקטע הוא שהנתון שמאפשר לי לטעון את זה, זה בעצם ש-f רציפה באפס ולכן זה אומר ש- מכך אני יודע שהגבול של f, כש-x שואף ל-0, קיים ולכן הגבולות החד צדדים של f קיימים. מפה אני טוען שהגבול הוא בעצם שווה ל-0 וזה רק לפתח הגדרתית את הגבולות החד צדדים ולהשתמש בנתון ש-
מכך אני יודע שהגבול של f, כש-x שואף ל-0, קיים ולכן הגבולות החד צדדים של f קיימים. מפה אני טוען שהגבול הוא בעצם שווה ל-0 וזה רק לפתח הגדרתית את הגבולות החד צדדים ולהשתמש בנתון ש-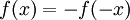 ובכך להראות שהטענה שהגבול שווה ל-0 נכונה. כלומר זה מה שחשבתי לעשות.
ובכך להראות שהטענה שהגבול שווה ל-0 נכונה. כלומר זה מה שחשבתי לעשות.
- בטענה 2 הגדרתי את X להיות קטן מאפס אבל אפשר שX יהיה גדול מאפס ואז באמת
תרגיל 8 שאלה 5
האם נתון ש-x>=0 ? תודה.
- (לא מתרגל) אין בתרגיל איזשהו X ספציפי. מה שכן אתה יכול די בקלות לדאוג לכך שהסביבה המנוקבת של 1 איתה תתעסק תהיה כך שכל x בה יהיה חיובי, ואם השאלה היא בנוגע להיות השורש מוגדר בסביבה אז עבור סביבה כנ"ל הפונקציה תהיה מוגדרת לכל x בסביבה המנוקבת. -לידור.א.- 16:34, 18 בדצמבר 2010 (IST)
- תודה, רק מה זה סביבה מנוקבת?
- סביבה מנוקבת של
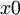 היא סביבה של
היא סביבה של 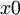 ללא
ללא 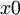 שקד רטר 18:23, 18 בדצמבר 2010 (IST)
שקד רטר 18:23, 18 בדצמבר 2010 (IST)
- סביבה מנוקבת של
- תודה, רק מה זה סביבה מנוקבת?
תרגיל 8 שאלה 6
נתון שהפונקציה מוגדרת וחסומה בקטע [0,1]. מה זה בדיוק אומר? האם זה אומר ש:
לכל x קיים  והוא שייך לקטע הזה?
והוא שייך לקטע הזה?