שיחה:88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/פונקציות/ערך הביניים
מתוך Math-Wiki
איך פותרים את תרגיל 4 ??
פתרון:
נגדיר לכל n את הפוקנציה הבאה ונרצה למצוא להן שורש:
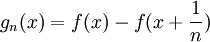
נשים לב שהפונקציה רציפה בתחחום ![[0,\frac{n-1}{n}]](/images/math/5/6/5/56553dbc6f303d109efdce12f333404b.png) , ולכן מקיימת את משפט ערך הביניים.
, ולכן מקיימת את משפט ערך הביניים.
נביט בערכים הבאים (אם אחד מהם שווה ל0, סיימנו):

נרצה למצוא שני איברים בתחום ההגדרה של הפונקציה 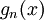 עם סימנים מנוגדים.
עם סימנים מנוגדים.
נבחין כי:
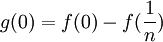
וכן כי מתקיים: 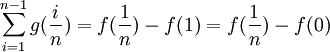
לפי משפט ערך הביניים קיים ![c\in [0,\frac{n-1}{n}]](/images/math/e/a/f/eaf8945dddfa4fe2985c08a963b8c7ad.png) כך שמתקיים:
כך שמתקיים:
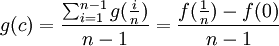
בבירור ניתן להבחין כי הסימנים של 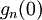 ושל
ושל 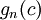 שונים, ולכן קיימת לפונקציה g שורש וסיימנו.
שונים, ולכן קיימת לפונקציה g שורש וסיימנו.
תודה, אכזרי ביותר.