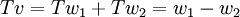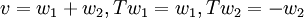אלגברה לינארית 1/מבחנים/פתרון מבחן דמה תשעא
תוכן עניינים
שאלה 1
שאלה 2
התרגיל בסוף מערך תרגול 7
שאלה 3
הפתרון נכון כל עוד המאפיין שונה מ-2
סעיף א
נניח כי v ניתן להצגה בצורה הנ"ל, וכך נחשב את w1,w2. לאחר שנחשב אותם, נוכיח שהם אכן מקיימים את התכונות הדרושות.
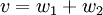 , נפעיל את T על שני האגפים לקבל
, נפעיל את T על שני האגפים לקבל
אם כן קיבלנו 2 משוואות בשני נעלמים, ואנו מחלצים מתוכן:
אם כן, לכל 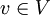 נגדיר
נגדיר 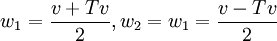 . קל לוודא שאכן מתקיים
. קל לוודא שאכן מתקיים
סעיף ב
נגדיר 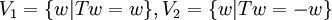 . נובע בקלות מסעיף א כי
. נובע בקלות מסעיף א כי 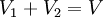 . אם נוכיח כי החיתוך בינהם הוא אפס, נקבל בקלות ממשפט המימדים כי
. אם נוכיח כי החיתוך בינהם הוא אפס, נקבל בקלות ממשפט המימדים כי 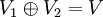 . אז איחוד הבסיסים בינהם יהווה בסיס העונה על דרישות התרגיל.
. אז איחוד הבסיסים בינהם יהווה בסיס העונה על דרישות התרגיל.
אבל אם וקטור w נמצא בחיתוך הוא מקיים w=-w ולכן w=0. משל.
שאלה 4
סעיף א
הפרכה:
סעיף ב
נניח כי 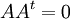 . נובע בקלות מהתרגיל שפתרנו במערך תרגול 2 כי A=0. כעת, נניח כי
. נובע בקלות מהתרגיל שפתרנו במערך תרגול 2 כי A=0. כעת, נניח כי 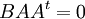 נכפול במשוחלפת של B ונקבל
נכפול במשוחלפת של B ונקבל 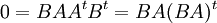 ואז שוב BA=0
ואז שוב BA=0
סעיף ג
הוכחה:
נובע ממשפט המימדים כי  לכן בלי הגבלת הכלליות ניתן להניח כי
לכן בלי הגבלת הכלליות ניתן להניח כי 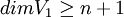 . באופן דומה
. באופן דומה 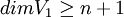 ומכיוון ש
ומכיוון ש 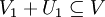 מתקיים לפי משפט המימדים כי
מתקיים לפי משפט המימדים כי 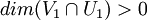 .
.
מכיוון שהסכום מכיל את כל החיתוכים האפשריים, זוג אחד מבינהם חייב להיות חיתוך לא אפס, ולכן הסכום אינו אפס.