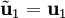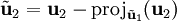אנליזת פורייה ויישומים קיץ תשעב/סיכומים/הרצאות/31.7.12
את נושא הקירוב לווקטורים לא סיימנו בשיעור הקודם ולכן השלמנו זאת ב־אנליזת פורייה ויישומים קיץ תשעב/סיכומים/הרצאות/31.7.12. חלק זה מופיע בסיכום השיעור הקודם ולא בדף הנוכחי.
תוכן עניינים
תהליך גרם־שמידט (Gram-Schmidt)
התהליך מייצר קבוצה אורתוגונלית/אורתונורמלית מקבוצה בת״ל כך שהן פורסות את אותו המרחב.
השלבים, ללא נרמול:
...
דוגמה
נתון בסיס 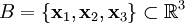 כאשר
כאשר 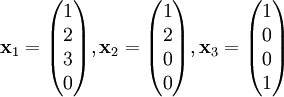 . ניצור באמצעותם בסיס אורתוגונלי:{{left|
. ניצור באמצעותם בסיס אורתוגונלי:{{left|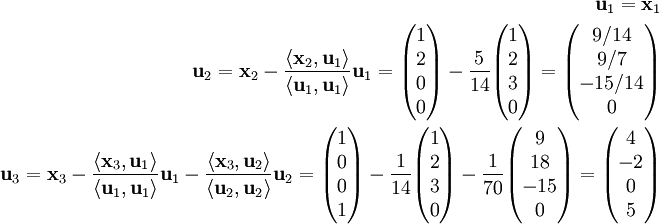 . נסים לב שהכפלנו כמה מהווקטורים בסקלר (14,5), מה שכמובן לא פגע באורתונורמליות.
. נסים לב שהכפלנו כמה מהווקטורים בסקלר (14,5), מה שכמובן לא פגע באורתונורמליות.
קיבלנו מערכת אורתונורמלית 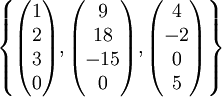 .
.
דוגמה נוספת
נתון מרחב פולינומים![P_n[x]](/images/math/9/6/7/967b23d5681e09247109d9acce668c46.png) הנפרש ע״י
הנפרש ע״י 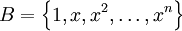 . נגדיר כפלה פנימית באופן הבא:
. נגדיר כפלה פנימית באופן הבא: 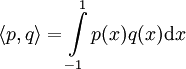 . נעזר בתהליך גרם־שמידט ונמצא מערכת אורתוגונילית:
. נעזר בתהליך גרם־שמידט ונמצא מערכת אורתוגונילית: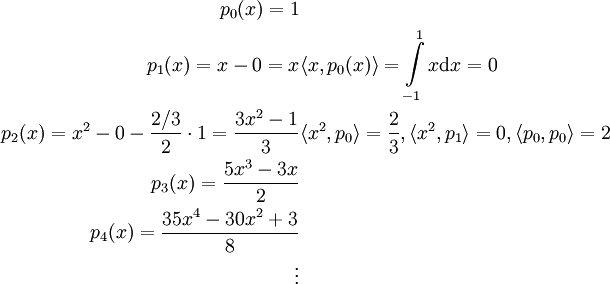
הערה: בסופו של התהליך מתקבלת סדרה של פולינומים אורתוגונליים הנקראים פולינומי לג׳נדר.
מתקיים 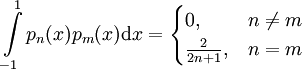 . בנוסף, קיימת נוסחה רקורסיבית
. בנוסף, קיימת נוסחה רקורסיבית 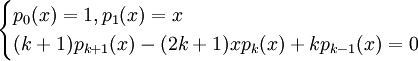 .
.
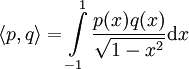 :
: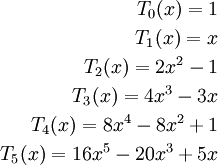
קיימת נוסחת רודריגז: 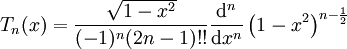 . נוסחה רקורסיבית:
. נוסחה רקורסיבית: 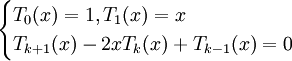 . מתקיים
. מתקיים 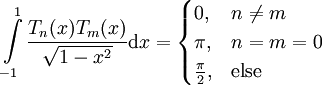 .
.
פולינומי לגר (Laguerre) נוצרים מ־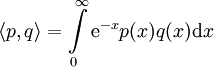 . נוסחתם הרקורסיבית:
. נוסחתם הרקורסיבית: 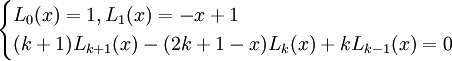
פולינומי הרמיט (Hermite): 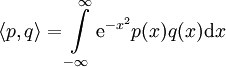 ו־
ו־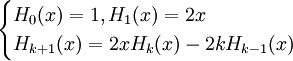 .
.
הערה: פולינומי לגר והרמיט לא יופיע במבחן.
תרגיל
מצא בסיס אורתונורמלי 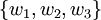 מהבסיס הבא:
מהבסיס הבא: 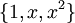 בקטע
בקטע ![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) בקרה של המכפלה הפנימית הסטנדרטית:
בקרה של המכפלה הפנימית הסטנדרטית: 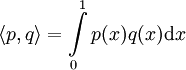 .
.
פתרון
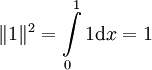 ולכן
ולכן 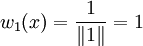 .
.
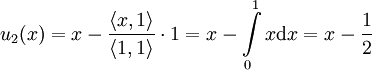 . עתה
. עתה 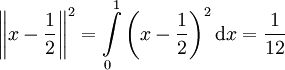 . לכן
. לכן 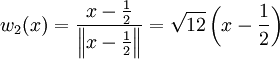 .
.
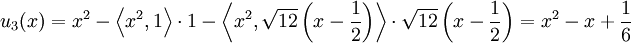 . ננרמל:
. ננרמל: 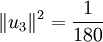 ולכן
ולכן 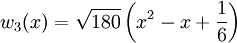
תרגיל
מצא קירוב ל־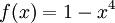 בעזרת 3 פולינומי לג׳נדר הראשונים בקטע
בעזרת 3 פולינומי לג׳נדר הראשונים בקטע ![[-1,1]](/images/math/d/0/6/d060b17b29e0dae91a1cac23ea62281a.png) .
.
פתרון
הקירוב מקיים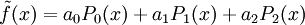 כאשר
כאשר 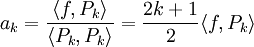 . נחשב:
. נחשב: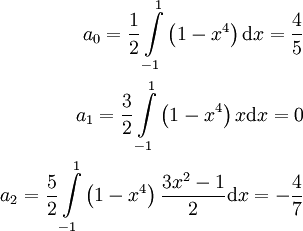
לכן 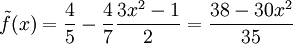 .
. 
תרגיל
מצא קירוב ל־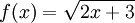 באמצעות 3 פולינומי לג׳נדר הראשונים בקטע
באמצעות 3 פולינומי לג׳נדר הראשונים בקטע ![[0,2]](/images/math/7/0/f/70fd3f388413505934da60b43afc4088.png) .
.
פתרון
דרך א: לחשב את פולינומי לג׳נדר בקטע ![[0,2]](/images/math/7/0/f/70fd3f388413505934da60b43afc4088.png) ולפתור כרגיל.
ולפתור כרגיל.
![[0,2]\to[-1,1]](/images/math/3/3/b/33b1312edb149f654647dad18127c1bf.png) . טרנספורמציה כזאת חייבת לקיים
. טרנספורמציה כזאת חייבת לקיים 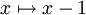 . לכן, כאשר
. לכן, כאשר 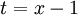 , מספיק לחשב קירוב ל־
, מספיק לחשב קירוב ל־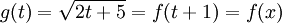 ב־
ב־![[-1,1]](/images/math/d/0/6/d060b17b29e0dae91a1cac23ea62281a.png) ואז נוכל למצוא קירוב ל־
ואז נוכל למצוא קירוב ל־ ב־
ב־![[0,2]](/images/math/7/0/f/70fd3f388413505934da60b43afc4088.png) :
: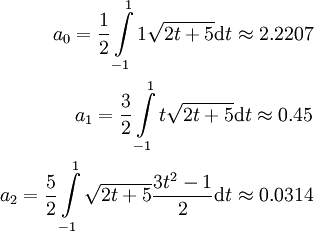
לכן 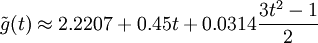 נציב
נציב 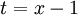 ולכן
ולכן 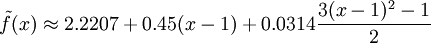 .
. 
הקדמה לשיעור הבא
נדון במכפלה הפנימית 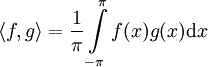 ונבדוק שהמערכת הבאה אורתונורמלית
ונבדוק שהמערכת הבאה אורתונורמלית 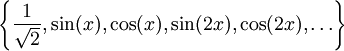 .
.