אנליזת פורייה ויישומים קיץ תשעב/סיכומים/תקציר
מתוך Math-Wiki
תוכן עניינים
להבא, אלא אם צוין אחרת, נסמן:
-
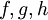 פונקציות.
פונקציות. - בהנתן
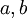 נסמן
נסמן 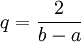 ו־
ו־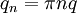 .
. -
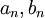 הם מקדמי פורייה של
הם מקדמי פורייה של 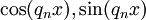 (בהתאמה) בטור פורייה של
(בהתאמה) בטור פורייה של  , ו־
, ו־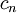 מקדמי פורייה של
מקדמי פורייה של 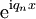 בטור פורייה המרוכב.
בטור פורייה המרוכב. -
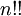 היא העצרת הכפולה של
היא העצרת הכפולה של  , והיא שווה למכפלת כל המספרים האי־זוגיים (אם
, והיא שווה למכפלת כל המספרים האי־זוגיים (אם  אי־זוגי) מ־1 עד
אי־זוגי) מ־1 עד  , או כל המספרים הזוגיים (אחרת). כלומר:
, או כל המספרים הזוגיים (אחרת). כלומר: 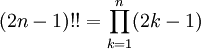 ו־
ו־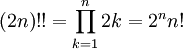 .
. -
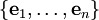 אורתונורמלית ו־
אורתונורמלית ו־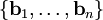 אורתוגונלית.
אורתוגונלית.
תזכורות ותוספות לאלגברה לינארית
- אי־שוויון הולדר: אם
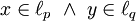 כאשר
כאשר 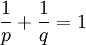 (כלומר,
(כלומר, 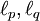 צמודים) אזי
צמודים) אזי 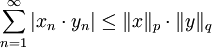 .
. - אם
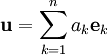 אזי
אזי 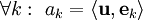 .
. - ההיטל של
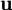 על
על 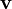 הוא
הוא 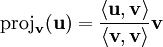 .
. - אם
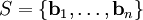 בסיס אורתוגונלי אזי הקירוב הטוב ביותר ל־
בסיס אורתוגונלי אזי הקירוב הטוב ביותר ל־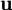 ב־
ב־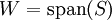 הוא
הוא 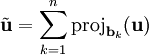 , כלומר
, כלומר 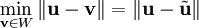 .
. - אי־שוויון בסל:
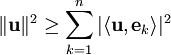 .
. - תהליך גרם–שמידט: בהנתן בסיס
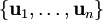 נוכל להגדיר בסיס אורתוגונלי
נוכל להגדיר בסיס אורתוגונלי 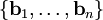 ובסיס אורתונורמלי
ובסיס אורתונורמלי 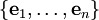 באופן הבא:
באופן הבא: 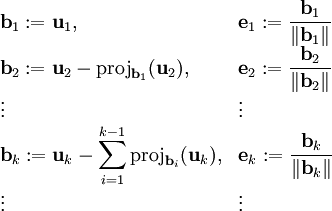
- מרחב הפולינומים ממעלה
 או פחות מסומן
או פחות מסומן ![P_n[x]](/images/math/9/6/7/967b23d5681e09247109d9acce668c46.png) .
. - פולינומי לז׳נדר: בהנתן המכפלה הפנימית
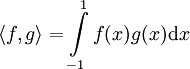 על מרחב הפולינומים
על מרחב הפולינומים ![P_n[x]](/images/math/9/6/7/967b23d5681e09247109d9acce668c46.png) , הפולינומים האורתוגונליים הנוצרים בתהליך גרם–שמידט מהבסיס
, הפולינומים האורתוגונליים הנוצרים בתהליך גרם–שמידט מהבסיס 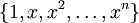 הם ניתן לחשב אותם גם ע״י
הם ניתן לחשב אותם גם ע״י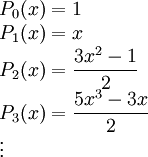
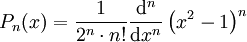 או
או 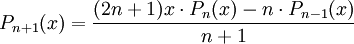 , והם מקיימים
, והם מקיימים 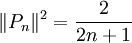 .
. - פולינומי צבישב: בהנתן המכפלה הפנימית
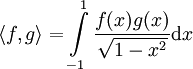 על מרחב הפולינומים
על מרחב הפולינומים ![P_n[x]](/images/math/9/6/7/967b23d5681e09247109d9acce668c46.png) , הפולינומים האורתוגונליים הנוצרים בתהליך גרם–שמידט מהבסיס
, הפולינומים האורתוגונליים הנוצרים בתהליך גרם–שמידט מהבסיס 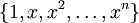 הם ניתן לחשב אותם גם ע״י
הם ניתן לחשב אותם גם ע״י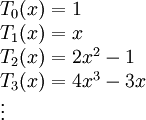
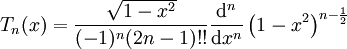 (נוסחת רודריגז) או
(נוסחת רודריגז) או 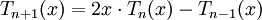 , והם מקיימים
, והם מקיימים 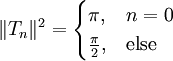 .
.
טורי פורייה
- פונקציה רציפה למקוטעין היא פונקציה רציפה למעט במספר סופי של נקודות אי־רציפות שאינן מסוג שני. הפונקציות הרציפות למקוטעין בקטע
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) יוצרות מרחב מכפלה פנימית
יוצרות מרחב מכפלה פנימית ![E[a,b]](/images/math/8/c/8/8c877957ea327bbcbccfc1d3fd3964ea.png) עם
עם 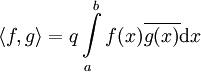 . מכפלה פנימית שימושית נוספת היא
. מכפלה פנימית שימושית נוספת היא 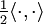 .
.
-
 הוא סימון מקוצר ל־
הוא סימון מקוצר ל־![E[-\pi,\pi]](/images/math/4/e/e/4ee004c8569267d13f31ce2a8af43e10.png) .
.
-
- מערכת סגורה: נתונה קבוצה אורתונורמלית אינסופית
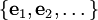 במרחב מכפלה פנימית. המערכת תקרא סגורה אם היא מקיימת לכל וקטור
במרחב מכפלה פנימית. המערכת תקרא סגורה אם היא מקיימת לכל וקטור 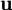 את התנאי
את התנאי 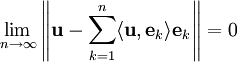 .
. - המערכות
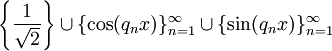 ו־
ו־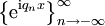 אורתונורמליות סגורות ב־
אורתונורמליות סגורות ב־![E[a,b]](/images/math/8/c/8/8c877957ea327bbcbccfc1d3fd3964ea.png) לפי המכפלות הפנימיות
לפי המכפלות הפנימיות 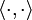 ו־
ו־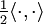 בהתאמה.
בהתאמה. - טור פורייה של
 ב־
ב־![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) הוא
הוא 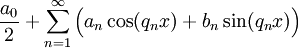 כאשר
כאשר 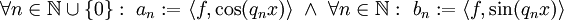 .
.
- אם
 זוגית זה טור קוסינוסים, ואם היא אי־זוגית זה טור סינוסים.
זוגית זה טור קוסינוסים, ואם היא אי־זוגית זה טור סינוסים. - מתקיים
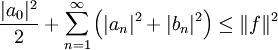 .
.
- אם
- טור פורייה המרוכב של
 ב־
ב־![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) הוא
הוא 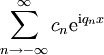 כאשר
כאשר 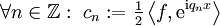 .
.
- מתקיים
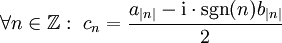 וכן
וכן 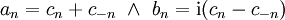 .
.
- מתקיים
- אם
![f\in E[a,b]](/images/math/6/b/5/6b512f992d20c255eb500cd49a84909c.png) ו־
ו־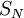 הסכום החלקי ה־
הסכום החלקי ה־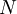 ־י של טור פורייה (מרוכב או ממשי) של
־י של טור פורייה (מרוכב או ממשי) של  , אזי
, אזי 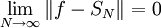 .
. -
![E'[a,b]](/images/math/a/6/c/a6cc496acd8b53eb4bcbcc6a24e63672.png) הוא מרחב כל הפוקנציות ב־
הוא מרחב כל הפוקנציות ב־![E[a,b]](/images/math/8/c/8/8c877957ea327bbcbccfc1d3fd3964ea.png) שקיימות להן הנגזרות החד־צדדיות בכל נקודה ב־
שקיימות להן הנגזרות החד־צדדיות בכל נקודה ב־![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) למעט, אולי, בקצות הקטע.
למעט, אולי, בקצות הקטע. - משפט ההתכנסות (משפט דיריכלה): תהי
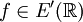 אינטגרבילית בהחלט ב־
אינטגרבילית בהחלט ב־![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ובעלת מחזור
ובעלת מחזור 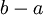 . בכל נקודה בה הפונקציה רציפה טור פורייה ב־
. בכל נקודה בה הפונקציה רציפה טור פורייה ב־![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) מתכנס ל־
מתכנס ל־ .
.
- אם
![f\in E'[c,d]](/images/math/b/f/5/bf5273fbb96011449a830d79f984292c.png) אזי ניתן ליצור המשכה מחזורית שלה ב־
אזי ניתן ליצור המשכה מחזורית שלה ב־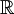 .
. - אם
 נקודת אי־רציפות אזי הטור מתכנס ל־
נקודת אי־רציפות אזי הטור מתכנס ל־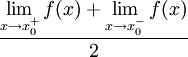 .
.
- תופעת גיבס: נניח שבנוסף
![f'\in E[a,b]](/images/math/6/e/a/6ead53d73f414d13abfb85e5c58441d7.png) ו־
ו־ נקודת אי־רציפות מסוג ראשון של
נקודת אי־רציפות מסוג ראשון של  כך ש־
כך ש־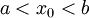 . כמו כן,
. כמו כן, 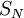 הסכום החלקי ה־
הסכום החלקי ה־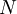 ־י של טור פורייה של
־י של טור פורייה של  . אזי קיימת סדרת נקודות
. אזי קיימת סדרת נקודות 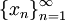 המקיימת
המקיימת 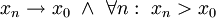 וכן
וכן 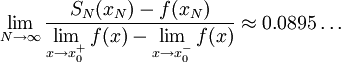 , וזו השגיאה המקסימלית.
, וזו השגיאה המקסימלית.
- תופעת גיבס: נניח שבנוסף
- אם
- למת רימן–לבג: אם
 אינטגרבילית בהחלט אזי
אינטגרבילית בהחלט אזי 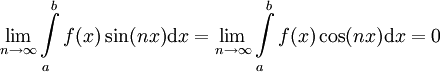 כאשר
כאשר 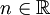 (זה גבול של פונקציה, ולא רק של סדרה).
(זה גבול של פונקציה, ולא רק של סדרה). - גרעין דיריכלה:
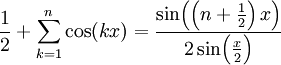 . בנוסף, האינטגרל של הביטוי ב־
. בנוסף, האינטגרל של הביטוי ב־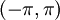 שווה ל־
שווה ל־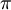 .
. - אם
![f\in E'[a,b]](/images/math/e/e/d/eed150b1c9c542a7b53ad99de6c1f8aa.png) רציפה ב־
רציפה ב־![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ו־
ו־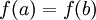 אז טור פורייה של
אז טור פורייה של  יתכנס אליה במ״ש על הקטע.
יתכנס אליה במ״ש על הקטע. - שוויון פרסבל: אם
![f\in E[a,b]](/images/math/6/b/5/6b512f992d20c255eb500cd49a84909c.png) אזי
אזי 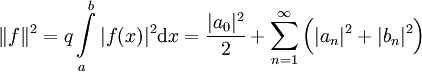 ו־
ו־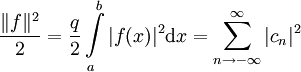 .
.
- שוויון פרסבל המוכלל: אם
![f,g\in E[a,b]](/images/math/e/4/0/e402ad926e5a0e7298de5ef2d34696ab.png) אזי
אזי 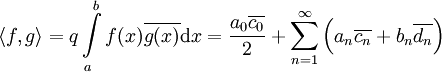 כאשר
כאשר 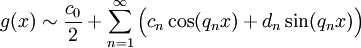 .
.
- שוויון פרסבל המוכלל: אם
- אם
 רציפה ב־
רציפה ב־![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ,
, 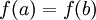 ו־
ו־![f'\in E[a,b]](/images/math/6/e/a/6ead53d73f414d13abfb85e5c58441d7.png) אזי טור פורייה של
אזי טור פורייה של  גזיר איבר־איבר ומתקיים
גזיר איבר־איבר ומתקיים 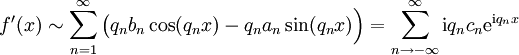 .
. - אם
![f\in E[a,b]](/images/math/6/b/5/6b512f992d20c255eb500cd49a84909c.png) אזי ניתן לבצע אינטגרציה איבר־איבר על טור פורייה. בנוסף, לכל
אזי ניתן לבצע אינטגרציה איבר־איבר על טור פורייה. בנוסף, לכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) ולכל
ולכל 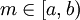 מתקייםוהטורים מתכנסים במ״ש.
מתקייםוהטורים מתכנסים במ״ש.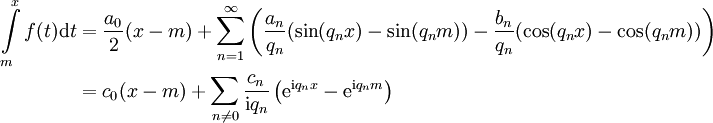
- אם
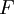 קדומה ל־
קדומה ל־ ב־
ב־![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אזי
אזי 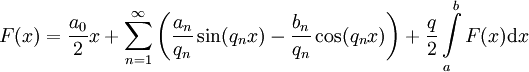 .
.
- אם
התמרות פורייה
-
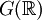 הוא המרחב הלינארי של כל הפונקציות המוגדרות מ־
הוא המרחב הלינארי של כל הפונקציות המוגדרות מ־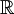 ל־
ל־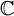 שהן רציפות למקוטעין ואינטגרביליות בהחלט ב־
שהן רציפות למקוטעין ואינטגרביליות בהחלט ב־ .
. - התמרת פורייה:
![\hat f=\mathcal F[f]:\mathbb R\to\mathbb C](/images/math/4/5/d/45d0bf7d35b904f9a2de9a7e9f3fc615.png) נקראת "התמרת פורייה של
נקראת "התמרת פורייה של  " ומוגדרת ע״י
" ומוגדרת ע״י 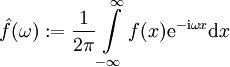 .
. - אם
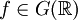 אזי
אזי 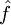 מוגדרת ורציפה בכל נקודה
מוגדרת ורציפה בכל נקודה 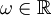 . בנוסף,
. בנוסף, 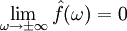 .
. - לכל
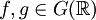 ולכל
ולכל 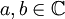 מתקיים:
מתקיים:
-
![\mathcal F[af+bg]=a\mathcal F[f]+b\mathcal F[g]](/images/math/2/3/1/231319837806bc8264ba00d77afdc8c1.png)
- אם
 ממשית אזי
ממשית אזי 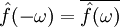 .
.
- מקרה פרטי: אם
 ממשית וזוגית אזי
ממשית וזוגית אזי 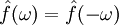 והיא פונקציה ממשית.
והיא פונקציה ממשית. - מקרה פרטי: אם
 ממשית ואי־זוגית אזי
ממשית ואי־זוגית אזי 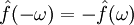 והיא פונקציה מדומה.
והיא פונקציה מדומה.
- מקרה פרטי: אם
- אם
 מדומה אזי
מדומה אזי 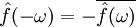 .
. - אם
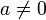 אזי
אזי =\frac1{|a|}\exp\!\left(\frac{\mathrm ib\omega}2\right)\mathcal F[f]\!\left(\frac\omega a\right)](/images/math/6/6/7/667f0e5def26c14a35d024c20d17ce30.png) .
. - אם
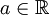 אזי
אזי ![\mathcal F\!\left[\mathrm e^{\mathrm iax}f(x)\right]\!(\omega)=\mathcal F[f](\omega-a)](/images/math/8/4/3/84309c1174205ea7de4f0aa70bd4a88a.png) .
. - אם
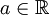 אזי
אזי =\frac{\mathcal F[f](\omega-a)-\mathcal F[f](\omega+a)}2](/images/math/e/d/e/ede44a7c1094be1352a69be51b3a2c95.png) .
. - אם
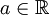 אזי
אזי =\frac{\mathcal F[f](\omega-a)-\mathcal F[f](\omega+a)}{2\mathrm i}](/images/math/5/3/d/53da1ddb139c41da1ad5a13f89269aa8.png) .
. - אם
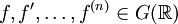 ו־
ו־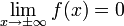 אזי
אזי ![\mathcal F\!\left[f^{(n)}\right]\!(\omega)=(\mathrm i\omega)^n\mathcal F[f](\omega)](/images/math/1/8/1/1817df68fce1def4137a440956634200.png) .
. - אם
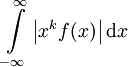 מתכנס לכל
מתכנס לכל 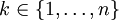 אזי
אזי 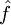 גזירה ברציפות
גזירה ברציפות  פעמים ומתקיים
פעמים ומתקיים ![\mathcal F\!\left[x^n f(x)\right]\!(\omega)=\mathrm i^n\frac{\mathrm d^n}{\mathrm d\omega^n}\mathcal F[f](\omega)](/images/math/9/3/d/93d1644649cb898b2c642c4276b7b698.png) .
.
-
- התמרת פורייה ההפוכה: אם
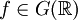 אזי בכל נקודה
אזי בכל נקודה  שבה קיימות הנגזרות החד־צדדיות מתקיים
שבה קיימות הנגזרות החד־צדדיות מתקיים 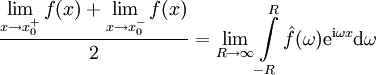 .
.
- מקרה פרטי: אם
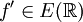 אזי
אזי 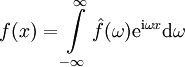 .
.
- מקרה פרטי: אם
- עקרון הדואליות של ההתמרה וההתמרה ההפוכה: תהי
 המקיימת
המקיימת 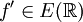 , ונרצה למצוא את התמרת פורייה של ההתמרה
, ונרצה למצוא את התמרת פורייה של ההתמרה 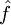 שלה. נוכל להציב
שלה. נוכל להציב 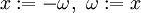 ב־
ב־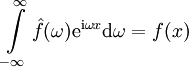 , לחלק את שני האגפים ב־
, לחלק את שני האגפים ב־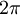 ולקבל
ולקבל 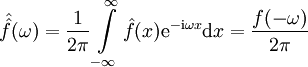 .
. - אם
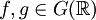 ו־
ו־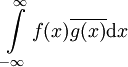 ו־
ו־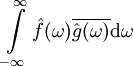 מתכנסים אזי
מתכנסים אזי 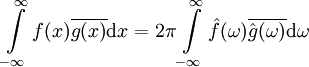 .
.
- מקרה פרטי: נוסחת פלנשרל (Plancherel): אם
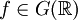 ו־
ו־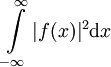 ו־
ו־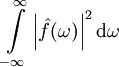 מתכנסים אזי
מתכנסים אזי 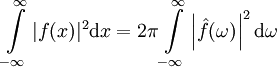 .
.
- מקרה פרטי: נוסחת פלנשרל (Plancherel): אם
- קונבולוציה: יהיו
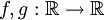 . אזי
. אזי 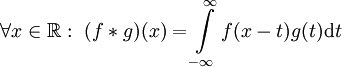 .
. -
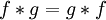
-
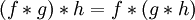
-
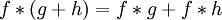
- אם
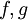 אינטגרביליות בהחלט אז
אינטגרביליות בהחלט אז 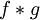 מוגדרת עבורן בכל
מוגדרת עבורן בכל 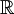 וגם היא אינטגרבילית בהחלט.
וגם היא אינטגרבילית בהחלט. - משפט הקונבולוציה:
![\forall f,g\in G(\mathbb R):\ \mathcal F[f*g]=2\pi\mathcal F[f]\mathcal F[g]](/images/math/e/d/0/ed0553cfdd3767d754aef28849b8ca40.png) .
.
- שימוש חשוב: נניח שידועות
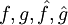 ונרצה למצוא
ונרצה למצוא 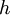 כך ש־
כך ש־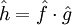 . אזי
. אזי 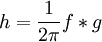 .
.
- שימוש חשוב: נניח שידועות
התמרות פורייה שימושיות
-
![\mathcal F\!\left[\mathrm e^{-|x|}\right]\!(\omega)=\frac1{\pi(1+\omega^2)}](/images/math/0/d/c/0dc3394e32977523af53d85b658861fb.png)
-
![\mathcal F\!\left[\mathrm e^{-x^2}\right]\!(\omega)=\frac{\mathrm e^{-\omega^2/4}}{2\sqrt\pi}](/images/math/5/9/5/595f0904da9f69e65fe5bd62c0f86eb2.png) (הוכחה ע״י חישוב הנגזרת של האינטגרל שמגדיר את ההתמרה ופתרון המד״ר המתקבלת:
(הוכחה ע״י חישוב הנגזרת של האינטגרל שמגדיר את ההתמרה ופתרון המד״ר המתקבלת: 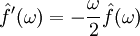 ).
). - עבור
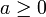 :
: ![\mathcal F[1_{[-a,a]}](\omega)=\frac{\sin(a\omega)}{\pi\omega}](/images/math/1/5/f/15f2f0dfb9b441a8bfb95c0a29921da9.png) (כאשר
(כאשר 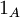 היא הפונקציה המציינת של קבוצה
היא הפונקציה המציינת של קבוצה  , ומוגדרת ע״י
, ומוגדרת ע״י 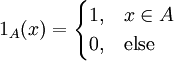 ).
).
התמרות לפלס
- חסימות מעריכית: נאמר ש־
 חסומה מעריכית אם קיימים
חסומה מעריכית אם קיימים 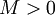 (חסם מעריכי) ו־
(חסם מעריכי) ו־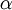 (סדר מעריכי) שעבורם
(סדר מעריכי) שעבורם 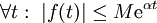 .
. -
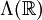 הוא המרחב הלינארי של פונקציות
הוא המרחב הלינארי של פונקציות 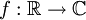 חסומות מעריכית כך ש־
חסומות מעריכית כך ש־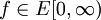 והן אינטגרביליות בהחלט ב־
והן אינטגרביליות בהחלט ב־![[0,R]](/images/math/1/8/8/188af55bd059c5460f58fe32fca2015d.png) לכל
לכל 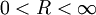 .
. - התמרת לפלס: תהי
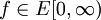 המקבלת ערכים ב־
המקבלת ערכים ב־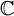 . אזי
. אזי ![\mathcal L[f]:\mathbb R\to\mathbb C](/images/math/b/4/7/b47320af82b478243522cb52bf958c5f.png) נקראת "התמרת לפלס של
נקראת "התמרת לפלס של  " ומוגדרת ע״י
" ומוגדרת ע״י =\int\limits_0^\infty f(t)\mathrm e^{-st}\mathrm dt](/images/math/9/d/b/9dbc448ca5313068d73dd714d71269fb.png) .
. - אם
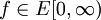 וחסומה מעריכית אזי
וחסומה מעריכית אזי =0](/images/math/1/5/b/15b74a1757a597f1584fe497a7f98671.png) .
. - אם
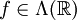 עם סדר מעריכי
עם סדר מעריכי 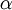 אז קיימת לה התמרת לפלס ב־
אז קיימת לה התמרת לפלס ב־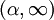 .
. -
![\forall a,b\in\mathbb C:\ \mathcal L[af+bg]=a\mathcal L[f]+b\mathcal L[g]](/images/math/0/2/d/02d5d0741c0864854123e73a8f181d0c.png)
-
![\mathcal L\!\left[t^n f(t)\right]\!(s)=(-1)^n\frac{\mathrm d^n}{\mathrm ds^n}\mathcal L[f](s)](/images/math/3/0/a/30a420c3513cae431ae2677a49f47c5a.png)
- משפט התמורה של הנגזרת: תהי
 עם חסם מעריכי
עם חסם מעריכי 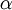 וכך ש־
וכך ש־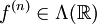 . אזי התמרת לפלס של
. אזי התמרת לפלס של 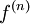 מוגדרת ב־
מוגדרת ב־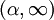 ומתקיים
ומתקיים ![\mathcal L\!\left[f^{(n)}\right]\!(s)=s^n\mathcal L[f](s)-\sum_{k=0}^{n-1} s^{n-1-k}f^{(k)}(0)](/images/math/e/2/c/e2c82220b62d7bc9e24a827ed1297ff7.png) .
. - קונבולוציה: יהיו
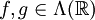 . אזי
. אזי 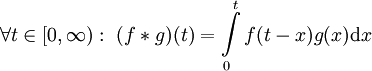 .
. - משפט הקונבולוציה:
![\forall f,g\in\Lambda(\mathbb R):\ \mathcal L[f*g]=\mathcal L[f]\mathcal L[g]](/images/math/6/f/f/6ff5a9e5cc40eeab68a301a31519ef6b.png) . אם בנוסף
. אם בנוסף 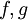 עם סדר מעריכי
עם סדר מעריכי 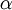 אז
אז ](/images/math/0/1/2/012ee18a7cdd18b6258c23db2a706f6d.png) מוגדר לכל
מוגדר לכל 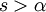 .
. - תהא
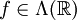 ונתונה
ונתונה 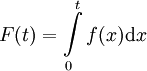 . ממשפט הקונבולוציה עם
. ממשפט הקונבולוציה עם 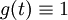 נקבל
נקבל =\frac{\mathcal L[f](s)}s](/images/math/6/b/e/6be5845fee7acd654b8627e50afb71ad.png) .
. - פונקציית הביסייד (Heaviside) היא
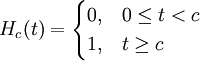 .
. -
=\mathrm e^{-cs}\mathcal L[f](s)](/images/math/4/f/9/4f9490b762534b0e76f2b9a7af5a1cdc.png)
התמרות לפלס שימושיות
בהתמרות הבאות,  הוא מספר ממשי כרצוננו.
הוא מספר ממשי כרצוננו.
דגימה והתמרת פורייה בדידה
-
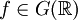 נקראת "חסומה בתדר" אם
נקראת "חסומה בתדר" אם 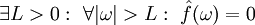 . ה־
. ה־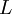 המינימלי שמקיים זאת נקרא "רוחב הפס" של
המינימלי שמקיים זאת נקרא "רוחב הפס" של  .
. - נניח כי
 חסומה בתדר ובעלת רוחב פס
חסומה בתדר ובעלת רוחב פס 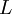 . אזי
. אזי 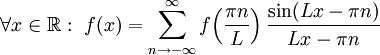 .
. - התמרת פורייה בדידה (DFT): בהינתן סדרה
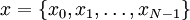 של
של 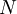 נקודות, נגדיר את התמרת פורייה הבדידה שלה ע״י
נקודות, נגדיר את התמרת פורייה הבדידה שלה ע״י 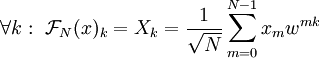 כאשר
כאשר 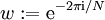 . זו התמרה של
. זו התמרה של 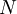 נקודות ל־
נקודות ל־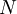 נקודות אחרות.
נקודות אחרות. - ההתמרת פורייה הבדידה ההפוכה (IDFT) נותנת את ערכי הסדרה המקורית
 לפי ערכי התמרת פורייה הבדידה
לפי ערכי התמרת פורייה הבדידה 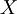 שלה:
שלה: 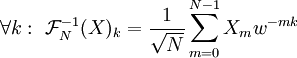 .
. -
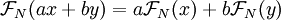
-
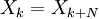
- קונבולוציה: בהנתן שתי סדרות
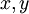 בעלות מחזור
בעלות מחזור 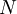 הקונבולוציה מוגדרת ע״י
הקונבולוציה מוגדרת ע״י 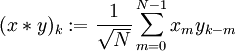 .
. - משפט הקונבולוציה:
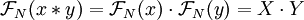 (כאשר הכפל מתבצע איבר־איבר).
(כאשר הכפל מתבצע איבר־איבר). - מטריצת DFT: התמרת פורייה הבדידה הינה לינארית, לכן קל להגדיר אותה באמצעות מטריצה
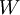 שתקיים
שתקיים 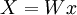 . המטריצה מוגדרת כ־
. המטריצה מוגדרת כ־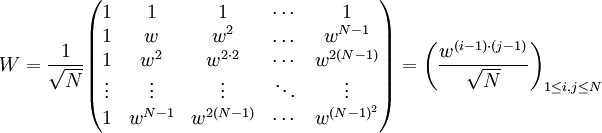 , וזו מטריצה יוניטרית (כלומר
, וזו מטריצה יוניטרית (כלומר 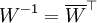 ) וסימטרית.
) וסימטרית. - FFT – Fast Fourier Transform: בעוד שחישוב על פי ההגדרה של התמרת פורייה בדידה הוא בעל סיבוכיות זמן ריצה
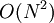 , תהליכי FFT עושים זאת ב־
, תהליכי FFT עושים זאת ב־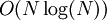 . יש מספר שיטות כאלו, אנו למדנו רק את תהליך Cooley–Tukey. הפירוט אינו מופיע כאן, אלא בקישור הנ״ל לוויקפדיה.
. יש מספר שיטות כאלו, אנו למדנו רק את תהליך Cooley–Tukey. הפירוט אינו מופיע כאן, אלא בקישור הנ״ל לוויקפדיה.
מד״ח
- מעבר חום: נתונה המד״ח
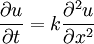 (
(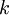 קבוע) עם תנאי ההתחלה
קבוע) עם תנאי ההתחלה 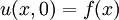 .
.
- שיטת הפרדת משתנים: אם נתונים בנוסף תנאי השפה
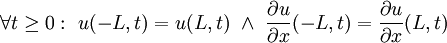 , נניח שניתן להציג את הפתרון
, נניח שניתן להציג את הפתרון 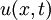 כמכפלה
כמכפלה 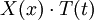 . אזי
. אזי 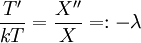 כאשר
כאשר  מספר חיובי (אם אי־חיובי תנאי השפה לא יתקיימו). מקבלים שתי מד״ר נפרדות:
מספר חיובי (אם אי־חיובי תנאי השפה לא יתקיימו). מקבלים שתי מד״ר נפרדות: 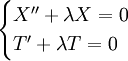 . לגבי המד״ר הראשונה, תנאי השפה דורשים ש־
. לגבי המד״ר הראשונה, תנאי השפה דורשים ש־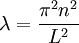 עבור
עבור 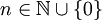 ולכן, עבור
ולכן, עבור  נתון,
נתון, 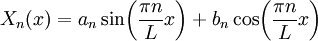 פתרון לכל
פתרון לכל 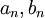 . לגבי המד״ר השנייה,
. לגבי המד״ר השנייה, 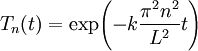 הוא פתרון עבור
הוא פתרון עבור  נתון. הפתרון הכללי של
נתון. הפתרון הכללי של 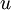 הוא צירוף לינארי של פתרונות הבסיס:
הוא צירוף לינארי של פתרונות הבסיס: 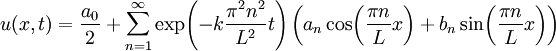 , כאשר מתנאי ההתחלה נובע ש־
, כאשר מתנאי ההתחלה נובע ש־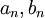 מקדמי טור פורייה של
מקדמי טור פורייה של  ב־
ב־![[-L,L]](/images/math/2/a/0/2a0da101a1b20a739aa871c2a9d89941.png) .
. - שימוש בהתמרת פורייה: נסמן
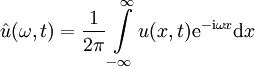 (כלומר, זו התמרת פורייה של
(כלומר, זו התמרת פורייה של 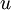 לפי
לפי  ). לפי המד״ח
). לפי המד״ח ![\frac{\partial\hat u}{\partial t}(\omega,t)=\frac k{2\pi}\int\limits_{-\infty}^\infty \frac{\partial^2 u}{\partial x^2}(x,t)\mathrm e^{-\mathrm i\omega x}\mathrm dx=k\mathcal F\!\left[\frac{\partial^2u}{\partial x^2}\right]\!(\omega,t)=k(\mathrm i\omega)^2\hat u(\omega,t)](/images/math/a/f/c/afc983aea05445d266c5b0716856377f.png) . פתרונה של המד״ר הזו הוא
. פתרונה של המד״ר הזו הוא 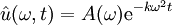 , והצבה של
, והצבה של 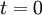 תתן
תתן 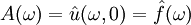 . עתה נחפש פונקציה
. עתה נחפש פונקציה 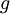 כך שהתמרת פורייה שלה לפי
כך שהתמרת פורייה שלה לפי  תהא
תהא 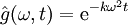 . לפי ההתמרה של
. לפי ההתמרה של 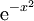 וכמה מתכונות ההתמרה נקבל
וכמה מתכונות ההתמרה נקבל 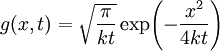 ולכן, לפי משפט הקונבולוציה,
ולכן, לפי משפט הקונבולוציה, 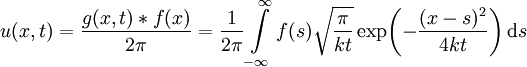 .
.
- שיטת הפרדת משתנים: אם נתונים בנוסף תנאי השפה
- משוואות גלים: נתונה המד״ח
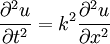 (
(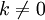 קבוע) עם תנאי ההתחלה
קבוע) עם תנאי ההתחלה 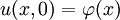 ו־
ו־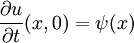 ותנאי שפה
ותנאי שפה 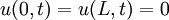 . נניח כי הפתרון מוצג כמכפלה
. נניח כי הפתרון מוצג כמכפלה 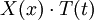 (שיטת הפרדת משתנים) ולכן
(שיטת הפרדת משתנים) ולכן 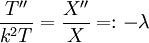 עבור
עבור  מספר חיובי. נקבל שתי מד״ר נפרדות:
מספר חיובי. נקבל שתי מד״ר נפרדות: 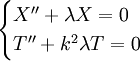 , ובאופן דומה למה שעשינו במשוואות מעבר חום נקבל
, ובאופן דומה למה שעשינו במשוואות מעבר חום נקבל 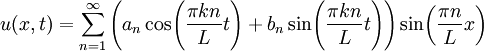 כאשר
כאשר 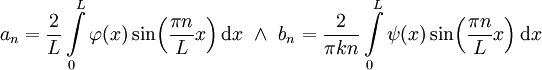 .
. - נתונה מד״ר לינארית עם מקדמים קבועים. נפעיל התמרת לפלס על אגפי המד״ר, נבודד את
![\mathcal L[y]](/images/math/d/a/f/daffcbd2fc6f0eb9bb9de352b4c0c7c4.png) (תוך שימוש בהתמרת הנגזרת ובנוסחאות אחרות) ונמצא את ההתמרה ההפוכה שלה.
(תוך שימוש בהתמרת הנגזרת ובנוסחאות אחרות) ונמצא את ההתמרה ההפוכה שלה.
![\mathcal L\!\left[\mathrm e^{at}\right]\!(s)=\frac1{s-a},\quad s>a](/images/math/8/a/1/8a142ece082f64db30931966b259374a.png)
![\mathcal L\!\left[t\mathrm e^{at}\right]\!(s)=\frac1{(s-a)^2},\quad s>a](/images/math/7/3/f/73fc3367b1518721a953bf23071dfce8.png)
=\frac a{s^2+a^2},\quad s>0](/images/math/a/b/d/abd1bc9f9416f389bc93c25ff43089c9.png)
=\frac s{s^2+a^2},\quad s>0](/images/math/1/d/2/1d2c18a5fdf715010d45f16708126ae7.png)
=\frac{\mathrm e^{-as}}s,\quad s>0](/images/math/e/b/7/eb7b39be0b8f6566a09724a85eff90bd.png)