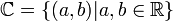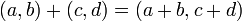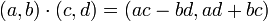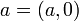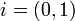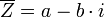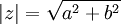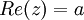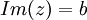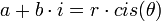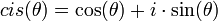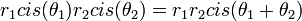הבדלים בין גרסאות בדף "אלגברה לינארית - ארז שיינר"
מתוך Math-Wiki
(←פרק 3 - אלגברת מטריצות) |
(←מטריצות הפיכות ומטריצות הופכיות) |
||
| שורה 190: | שורה 190: | ||
===מטריצות הפיכות ומטריצות הופכיות=== | ===מטריצות הפיכות ומטריצות הופכיות=== | ||
<videoflash>mDGV4RgivKw</videoflash> | <videoflash>mDGV4RgivKw</videoflash> | ||
| + | |||
| + | <videoflash>yMNcwMg5TFI</videoflash> | ||
גרסה מ־06:12, 11 ביולי 2020
תוכן עניינים
- 1 חומר עזר
- 2 סרטוני ותקציר הרצאות
- 2.1 פרק 1 - שדות
- 2.2 פרק 2- מערכות משוואות לינאריות
- 2.2.1 מבוא למטריצות ולמערכות משוואות לינאריות
- 2.2.2 הגדרת מערכת משוואות לינארית וקבוצת פתרונות
- 2.2.3 פעולות דירוג אלמנטריות
- 2.2.4 ייצוג מערכת משוואות בעזרת מטריצה
- 2.2.5 צורה מדורגת וצורה מדורגת קנונית
- 2.2.6 משתנים חופשיים ותלויים
- 2.2.7 דירוג מטריצה עם פרמטר
- 2.2.8 הוכחת קיום ויחידות צורה מדורגת קנונית
- 2.2.9 תרגול
- 2.3 פרק 3 - אלגברת מטריצות
- 2.4 פרק 4 - מרחבים וקטוריים
- 2.5 פרק 5 - העתקות לינאריות
- 2.6 פרק 6 - דטרמיננטות
חומר עזר
סרטוני ותקציר הרצאות
פרק 1 - שדות
הגדרה ותכונות של שדה
- שדה הוא קבוצה
 יחד עם שתי פעולות
יחד עם שתי פעולות 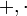 כך שמתקיימות התכונות הבאות:
כך שמתקיימות התכונות הבאות:
- סגירות: לכל
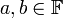 מתקיים כי
מתקיים כי 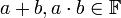
- קומוטטיביות (חילופיות): לכל
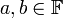 מתקיים כי
מתקיים כי 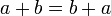 וכן
וכן 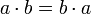
- אסוציאטיביות (קיבוץ): לכל
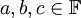 מתקיים כי
מתקיים כי 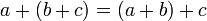 וכן
וכן 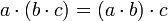
- נייטרליים: קיימים
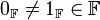 כך שלכל
כך שלכל 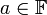 מתקיים כי
מתקיים כי 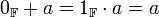
- נגדיים: לכל
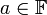 קיים נגדי
קיים נגדי 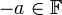 כך ש
כך ש 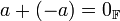
- הופכיים: לכל
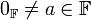 קיים הופכי
קיים הופכי 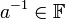 כך ש
כך ש 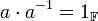
- דיסטריביוטיביות (פילוג): לכל
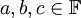 מתקיים כי
מתקיים כי 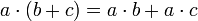
- יהי שדה
 אזי לכל
אזי לכל 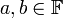 מתקיים כי
מתקיים כי 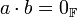 אם ורק אם
אם ורק אם 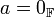 או
או 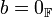
- תכונות נוספות של שדות
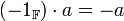
- אם
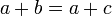 אזי
אזי 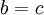
- אם
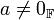 וגם
וגם 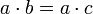 אזי
אזי 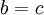
שדות סופיים
שדה המרוכבים
הגדרת המספרים המרוכבים
- נסמן
- נובע כי
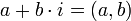
- הגדרות עבור
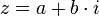
- תכונות
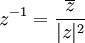 אם
אם 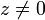
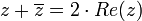
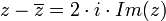
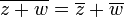
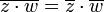
צורה קרטזית וצורה קוטבית (פולרית)
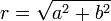
- עבור הזוית נחלק למקרים:
- אם
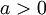 אזי
אזי 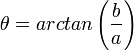
- אם
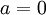 וגם
וגם 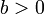 אזי
אזי 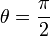
- אם
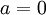 וגם
וגם 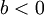 אזי
אזי 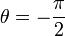
- אם
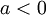 אזי
אזי 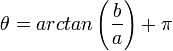
- אם
- עבור
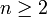 טבעי, ומספר מרוכב
טבעי, ומספר מרוכב 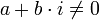 קיימים בדיוק n פתרונות למשוואה
קיימים בדיוק n פתרונות למשוואה 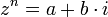
- הנוסחא למציאת כל הפתרונות השונים:
- נעביר את המספר לצורתו הקוטבית
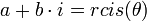
- הפתרונות הם
![z_k = \sqrt[n]{r} cis\left(\frac{\theta+2\pi k}{n}\right)](/images/math/4/0/a/40a498b3800d11f992177f92edca3fac.png) עבור
עבור 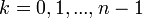
- נעביר את המספר לצורתו הקוטבית
תרגול
פרק 2- מערכות משוואות לינאריות
מבוא למטריצות ולמערכות משוואות לינאריות
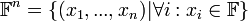 קבוצת הn-יות הסדורות.
קבוצת הn-יות הסדורות.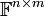 קבוצת המטריצות עם n שורות וm עמודות, ואיברים מהשדה
קבוצת המטריצות עם n שורות וm עמודות, ואיברים מהשדה 
הגדרת מערכת משוואות לינארית וקבוצת פתרונות
פעולות דירוג אלמנטריות
ייצוג מערכת משוואות בעזרת מטריצה
צורה מדורגת וצורה מדורגת קנונית
משתנים חופשיים ותלויים
דירוג מטריצה עם פרמטר
הוכחת קיום ויחידות צורה מדורגת קנונית
תרגול
פרק 3 - אלגברת מטריצות
חיבור מטריצות וכפל בסקלר
כפל מטריצות
שיטות לחישוב כפל מטריצות
תכונות של אלגברת מטריצות
פתרון כללי למערכת משוואות לא הומוגנית
- פתרון פרטי למערכת הלא הומוגנית + פתרון כללי למערכת ההומוגנית = פתרון כללי למערכת הלא הומוגנית
שחלוף
עקבה
תרגול
מטריצות הפיכות ומטריצות הופכיות
מטריצות פעולה
תרגול
תרגול בנושא מטריצות הפיכות ומטריצות פעולה
פרק 4 - מרחבים וקטוריים
הגדרה ותכונות של מרחבים וקטוריים
תתי מרחבים
חיתוך, סכום, וסכום ישר של תתי מרחבים
תרגול
פרישה ותלות לינארית
בסיס ומימד
משפט השלישי חינם
תרגול
משפט המימדים
תרגול
הצגה פרמטרית ואלגברית
שלושת מרחבי המטריצה ודרגת מטריצה
תרגול
פרק 5 - העתקות לינאריות
העתקות, הרכבת העתקות, הפיכות העתקות
- מרחב ההעתקות
גרעין ותמונה
משפט הדרגה
תרגול
מטריצה מייצגת העתקה
יחידות הצגה לפי בסיס, קואורדינטות
משפט קיום ויחידות
מטריצת סכום והרכבה
מטריצות מעבר בין בסיסים
תרגול
- תרגול המכיל קואורדינטות ומטריצות מעבר בין בסיסים
- תרגול בנושא מטריצות מייצגות העתקות
- תרגול נוסף בנושא העתקות