הבדלים בין גרסאות בדף "אלגברה לינארית - ארז שיינר"
מתוך Math-Wiki
(←יחידות הצגה לפי בסיס ומשפט ההגדרה) |
(←הגדרה ותכונות של מרחבים וקטוריים) |
||
| (46 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
=חומר עזר= | =חומר עזר= | ||
*[[מדיה:16Linear1Orit.pdf|סיכומי ההרצאות של ד״ר ארז שיינר, ע״י אורית חסון, קיץ 2016]] | *[[מדיה:16Linear1Orit.pdf|סיכומי ההרצאות של ד״ר ארז שיינר, ע״י אורית חסון, קיץ 2016]] | ||
| − | *[[אלגברה לינארית 1/מבחנים|מבחנים ובחנים באלגברה לינארית 1]] | + | *[[אלגברה לינארית 1/מבחנים|מבחנים ובחנים עם פתרונות מלאים באלגברה לינארית 1]] |
=סרטוני ותקציר הרצאות= | =סרטוני ותקציר הרצאות= | ||
| + | [https://www.youtube.com/playlist?list=PLHinTfsAOC-s2FLlORO26_lglSVhtF-Fy פלייליסט של כל הסרטונים] | ||
| + | |||
| + | |||
==פרק 1 - שדות== | ==פרק 1 - שדות== | ||
===הגדרה ותכונות של שדה=== | ===הגדרה ותכונות של שדה=== | ||
| שורה 36: | שורה 39: | ||
====הגדרת המספרים המרוכבים==== | ====הגדרת המספרים המרוכבים==== | ||
*<math>\mathbb{C}=\{(a,b)|a,b\in\mathbb{R}\}</math> | *<math>\mathbb{C}=\{(a,b)|a,b\in\mathbb{R}\}</math> | ||
| − | *<math>(a,b)+(c,d)=(a+ | + | *<math>(a,b)+(c,d)=(a+c,b+d)</math> |
*<math>(a,b)\cdot (c,d)=(ac-bd,ad+bc)</math> | *<math>(a,b)\cdot (c,d)=(ac-bd,ad+bc)</math> | ||
| שורה 49: | שורה 52: | ||
*הגדרות עבור <math>z=a+b\cdot i</math> | *הגדרות עבור <math>z=a+b\cdot i</math> | ||
| − | **<math>\overline{ | + | **<math>\overline{z}=a-b\cdot i</math> |
**<math>|z|=\sqrt{a^2+b^2}</math> | **<math>|z|=\sqrt{a^2+b^2}</math> | ||
**<math>Re(z)=a</math> | **<math>Re(z)=a</math> | ||
| שורה 247: | שורה 250: | ||
*<math>\alpha(AB) = (\alpha A)B = A (\alpha B)</math> | *<math>\alpha(AB) = (\alpha A)B = A (\alpha B)</math> | ||
*<math>(\alpha+\beta)A = \alpha A+\beta A</math> וכן <math>\alpha(A+B)=\alpha A + \alpha B</math> | *<math>(\alpha+\beta)A = \alpha A+\beta A</math> וכן <math>\alpha(A+B)=\alpha A + \alpha B</math> | ||
| + | *<math>(\alpha \beta)A=\alpha(\beta A)</math> | ||
| שורה 299: | שורה 303: | ||
| − | *דוגמא: לא קיימות מטריצות | + | *דוגמא: לא קיימות מטריצות ממשיות <math>A,B\in\mathbb{R}^{n\times n}</math> כך ש <math>AB-BA=I</math> |
**<math>tr(AB-BA)=0</math> אך <math>tr(I)=n\neq 0</math> | **<math>tr(AB-BA)=0</math> אך <math>tr(I)=n\neq 0</math> | ||
| שורה 385: | שורה 389: | ||
*מרחב וקטורי <math>V</math> מעל שדה <math>\mathbb{F}</math> הוא קבוצת איברים (הנקראים וקטורים) יחד עם פעולת חיבור וכפל בסקלר, כך שמתקיימות התכונות הבאות: | *מרחב וקטורי <math>V</math> מעל שדה <math>\mathbb{F}</math> הוא קבוצת איברים (הנקראים וקטורים) יחד עם פעולת חיבור וכפל בסקלר, כך שמתקיימות התכונות הבאות: | ||
#סגירות: <math>\forall u,w\in V\forall \alpha\in\mathbb{F}:u+w\in V \and \alpha u\in V</math> | #סגירות: <math>\forall u,w\in V\forall \alpha\in\mathbb{F}:u+w\in V \and \alpha u\in V</math> | ||
| − | #חילופיות: <math>\forall u,w\in V | + | #חילופיות: <math>\forall u,w\in V:u+w=w+u</math> |
#אסוציאטיביות (קיבוץ): <math>\forall u,w,v\in V\forall \alpha,\beta\in\mathbb{F}:(u+w)+v=u+(w+v) \and \alpha(\beta v) = (\alpha \beta) v</math> | #אסוציאטיביות (קיבוץ): <math>\forall u,w,v\in V\forall \alpha,\beta\in\mathbb{F}:(u+w)+v=u+(w+v) \and \alpha(\beta v) = (\alpha \beta) v</math> | ||
#נייטרלי לחיבור: <math>\exists 0_V\in V\forall v\in V:0_V+v=v</math> | #נייטרלי לחיבור: <math>\exists 0_V\in V\forall v\in V:0_V+v=v</math> | ||
| שורה 402: | שורה 406: | ||
<videoflash>OLYp1kVAPrA</videoflash> | <videoflash>OLYp1kVAPrA</videoflash> | ||
| − | |||
===תתי מרחבים=== | ===תתי מרחבים=== | ||
| שורה 556: | שורה 559: | ||
<videoflash>UR9LnbO4QGE</videoflash> | <videoflash>UR9LnbO4QGE</videoflash> | ||
| + | |||
| + | ====העשרה==== | ||
| + | |||
| + | *לכל מרחב וקטורי יש בסיס. | ||
| + | *ניקח שרשרת מקסימלית של קבוצות בת"ל M. | ||
| + | *נגדיר את האיחוד הכללי של M להיות B. | ||
| + | *B בת"ל, כי אם יש בה וקטורים תלויים, הם הגיעו מאחד הקבוצות (בשרשרת כל מספר סופי של קבוצות מוכלות באחת מהן) | ||
| + | *B פורשת, אחרת היה ניתן להגדיל אותה באמצעות וקטור שאינו נפרש על ידה, היינו מקבלים קבוצה בת"ל חדשה שניתן להוסיף לשרשרת המקסימלית, בסתירה. | ||
| + | |||
| + | |||
| + | <videoflash>qzUDzq2pB1Q</videoflash> | ||
====משפט השלישי חינם==== | ====משפט השלישי חינם==== | ||
| שורה 613: | שורה 627: | ||
<videoflash>WWcHqqshzlo</videoflash> | <videoflash>WWcHqqshzlo</videoflash> | ||
| + | |||
| + | |||
| + | *על מנת למצוא בסיס לחיתוך בין תתי מרחבים, נציג את שניהם בצורה אלגברית והחיתוך הוא אוסף הפתרונות של המשוואות משתי המערכות. | ||
| + | *על מנת למצוא בסיס לסכום תתי מרחבים, נציג את שניהם בצורה פרמטרית והסכום נפרש ע"י איחוד הקבוצות הפורשות. | ||
<videoflash>W3jcV4O-FLc</videoflash> | <videoflash>W3jcV4O-FLc</videoflash> | ||
| + | |||
| + | |||
| + | *ניתן להשלים כל קבוצה בת"ל לבסיס. | ||
| + | *לוקחים את הקבוצה הבת"ל, מוסיפים לה בסיס כלשהו, מדרגים בעמודות ומוחקים את הוקטורים המיותרים. | ||
<videoflash>XKutm8q2elw</videoflash> | <videoflash>XKutm8q2elw</videoflash> | ||
| + | |||
====תרגול==== | ====תרגול==== | ||
*[[88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/7|תרגול בנושא מרחבי המטריצה]] | *[[88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/7|תרגול בנושא מרחבי המטריצה]] | ||
| − | |||
===דרגה של מטריצה=== | ===דרגה של מטריצה=== | ||
| + | |||
| + | *בכל צורה מדורגת של A, האיברים הפותחים נמצאים באותן העמודות. | ||
| + | |||
<videoflash>pMNQF8yucGs</videoflash> | <videoflash>pMNQF8yucGs</videoflash> | ||
| + | |||
| + | |||
| + | *כל הגדלים הבאים שווים: | ||
| + | **דרגה של מטריצה | ||
| + | **מימד מרחב העמודות | ||
| + | **מימד מרחב השורות | ||
| + | **מספר השורות השונות מאפס בצורה המדורגת | ||
| + | **מספר המשתנים התלויים במערכת ההומוגנית | ||
| + | |||
| + | |||
| + | *כמו כן, מימד מרחב האפס שווה למספר המשתנים החופשיים. | ||
| + | |||
| + | |||
| + | *ביחד מקבלים את משפט הדרגה (שנוכיח במדויק בהמשך): דרגת המטריצה ועוד מימד מרחב האפס שווה לכמות עמודות המטריצה (מספר המשתנים). | ||
| שורה 674: | שורה 713: | ||
====משפט הדרגה להעתקות לינאריות ולמטריצות==== | ====משפט הדרגה להעתקות לינאריות ולמטריצות==== | ||
| + | |||
| + | *תהי העתקה לינארית <math>T:V\to W</math> ויהי <math>\{v_1,...,v_n\}</math> בסיס לV. | ||
| + | *אזי <math>Im T=span\{Tv_1,...,Tv_n\}</math> | ||
| שורה 686: | שורה 728: | ||
<videoflash>iJWnxV8jZ3A</videoflash> | <videoflash>iJWnxV8jZ3A</videoflash> | ||
| + | |||
| + | |||
| + | *תהי <math>T:V\to W</math> העתקה לינארית בין מרחבים וקטוריים נוצרים סופית. | ||
| + | **אם T חח"ע אז <math>\dim V\leq \dim W</math> | ||
| + | **אם T על אזי <math>\dim V \geq \dim W</math> | ||
| + | **אם <math>\dim V = \dim W</math> אזי T חח"ע אם"ם T על. | ||
| + | |||
| + | |||
| + | *העתקה לינארית נקראת גם '''הומומורפיזם'''. העתקה לינארית הפיכה נקראת '''איזומורפיזם'''. | ||
| + | *מרחבים וקטוריים נקראים '''איזומורפייים''' זה לזה, אם קיים איזומורפיזם בינהם (זהו יחס שקילות). | ||
| + | *מרחבים וקטוריים נוצרים סופית איזומורפיים זה לזה, אם ורק אם המימדים שלהם שווים. | ||
| + | |||
| + | |||
| + | <videoflash>Y-NJvNQWFzM</videoflash> | ||
====תרגול==== | ====תרגול==== | ||
| שורה 691: | שורה 747: | ||
===יחידות הצגה לפי בסיס ומשפט ההגדרה=== | ===יחידות הצגה לפי בסיס ומשפט ההגדרה=== | ||
| + | |||
| + | *יהי V מ"ו ויהי <math>\{v_1,...,v_n\}</math> בסיס סדור לV. | ||
| + | *אזי לכל <math>x\in V</math> '''קיימת''' הצגה '''יחידה''' כצירוף לינארי של איברי הבסיס: | ||
| + | **<math>x=a_1v_1+...+a_nv_n</math> | ||
| + | |||
| + | |||
<videoflash>qzvrMPhp3eY</videoflash> | <videoflash>qzvrMPhp3eY</videoflash> | ||
| + | |||
| + | |||
| + | *יהיו V,W מ"ו מעל אותו שדה, ויהי <math>\{v_1,...,v_n\}</math> בסיס סדור לV. | ||
| + | *תהיינה סדרת וקטורים <math>w_1,...,w_n\in W</math> לאו דווקא שונים. | ||
| + | *אזי '''קיימת''' העתקה לינארית '''יחידה''' <math>T:V\to W</math> המקיימת: | ||
| + | **לכל i מתקיים כי <math>Tv_i=w_i</math> | ||
| שורה 697: | שורה 765: | ||
===מטריצה מייצגת העתקה=== | ===מטריצה מייצגת העתקה=== | ||
| + | <videoflash>IOYMxNgkQoY</videoflash> | ||
| + | |||
====קואורדינטות==== | ====קואורדינטות==== | ||
| + | |||
| + | *יהי V מ"ו ויהי <math>B=\{v_1,...,v_n\}</math> בסיס סדור לV. | ||
| + | *לכל <math>v\in V</math> נגדיר את '''וקטור הקואורדינטות לפי B''' להיות הסקלים מההצגה היחידה: | ||
| + | **<math>[v]_B=\begin{pmatrix}\alpha_1 \\ \vdots \\ \alpha_n\end{pmatrix}</math> אם ורק אם <math>v=\alpha_1v_1+...+\alpha_nv_n</math> | ||
| + | |||
| + | |||
| + | *מה עושים עם הקואורדינטות? כופלים באיברי הבסיס! | ||
| + | |||
| + | |||
| + | <videoflash>wi8TNSA5Los</videoflash> | ||
| + | |||
| + | |||
| + | *נגדיר פונקציה <math>T:V\to \mathbb{F}^n</math> ע"י <math>Tv=[v]_B</math>, אזי T היא איזומורפיזם. לכן | ||
| + | **<math>[a_1u_1+...+a_ku_k]_B=a_1[u_1]_B+...+a_k[u_k]_B</math> | ||
| + | **הסדרה <math>u_1,...,u_k\in V</math> בת"ל אם ורק אם הסדרה <math>[u_1]_B,...,[u_k]_B</math> בת"ל | ||
| + | **<math>v\in span\{u_1,...,u_k\}</math> אם ורק אם <math>[v]_B\in span \{[u_1]_B,...,[u_k]_B\}</math> | ||
| + | |||
| + | |||
| + | <videoflash>VSpBzsMVgMw</videoflash> | ||
====משפט קיום ויחידות==== | ====משפט קיום ויחידות==== | ||
| + | *יהיו <math>V,W</math> מ"ו מעל אותו שדה <math>\mathbb{F}</math>. | ||
| + | *נניח V ממימד n וB בסיס סדור שלו. | ||
| + | *נניח W ממימד m וC בסיס סדור שלו. | ||
| + | *תהי <math>T:V\to W</math> העתקה לינארית. | ||
| + | *אזי: | ||
| + | **'''קיימת''' מטריצה '''יחידה''' <math>[T]_C^B\in\mathbb{F}^{m\times n}</math> המקיימת: | ||
| + | **לכל <math>v\in V</math> מתקיים כי <math>[T]_C^B[v]_B=[Tv]_C</math> | ||
| − | ==== | + | |
| + | |||
| + | *על מנת למצוא את המטריצה המייצגת: | ||
| + | **נפעיל את ההעתקה על איברי הבסיס של התחום. | ||
| + | **נמצא את הקואורדינטות של תמונות איברי בסיס התחום לפי בסיס הטווח. | ||
| + | **נשים את וקטורי הקואורדינטות שמצאנו בעמודות ונקבל את המטריצה המייצגת. | ||
| + | |||
| + | |||
| + | *<math>[T]_C^B= \begin{pmatrix}| & & | \\ \left[T v_1 \right]_C & \cdots & \left[ T v_n \right]_C \\ | & & | \end{pmatrix} \in \mathbb{F}^{m\times n}</math> | ||
| + | |||
| + | |||
| + | |||
| + | <videoflash>iglkE9qqy84</videoflash> | ||
| + | |||
| + | ====המטריצה המייצגת את ההעתקה ההופכית==== | ||
| + | |||
| + | *יהיו <math>V,W</math> מ"ו ממימד סופי מעל השדה <math>\mathbb{F}</math> עם בסיסים <math>B,C</math> בהתאמה. | ||
| + | *תהי <math>T:V\to W</math> העתקה לינארית, ויהי סקלר <math>\alpha\in\mathbb{F}</math> | ||
| + | *אזי | ||
| + | **<math>[T+S]^B_C=[T]^B_C+[S]^B_C</math> | ||
| + | **<math>[\alpha T]^B_C=\alpha[T]^B_C</math> | ||
| + | **<math>[S\circ T]_D^B=[S]^C_D[T]_C^B</math> | ||
| + | **ההעתקה T הפיכה אם ורק אם המטריצה המייצגת <math>[T]^B_C</math> הפיכה | ||
| + | ***אם ההעתקה הפיכה, מתקיים כי <math>[T^{-1}]^C_B = \left([T]^B_C\right)^{-1}</math> | ||
| + | |||
| + | |||
| + | |||
| + | <videoflash>EYU0bMBYEJM</videoflash> | ||
====מטריצות מעבר בין בסיסים==== | ====מטריצות מעבר בין בסיסים==== | ||
| + | *<math>[I]_{C_2}^{C_1}[T]_{C_1}^{B_1}[I]_{B_1}^{B_2}=[T]_{C_2}^{B_2}</math> | ||
| + | *<math>\left([I]_C^B\right)^{-1}=[I]_B^C</math> | ||
| + | |||
| + | |||
| + | <videoflash>FIoJr-dRk9Y</videoflash> | ||
| + | |||
| + | ===שלוש צורות הצגת ההעתקה=== | ||
| + | *ניתן להציג העתקה לינארית בשלוש דרכים: | ||
| + | **נוסחא מפורשת | ||
| + | **לפי בסיס | ||
| + | **בעזרת מטריצה מייצגת | ||
| + | |||
| + | |||
| + | <videoflash>ouEdwylqPiQ</videoflash> | ||
| + | |||
=====תרגול===== | =====תרגול===== | ||
| שורה 714: | שורה 852: | ||
===תמורות=== | ===תמורות=== | ||
| − | + | *נגדיר את אוסף התמורות <math>S_n</math> להיות קבוצת כל הפונקציות ההפיכות מהקבוצה <math>\{1,2,...,n\}</math> לעצמה. | |
| − | |||
| − | = | + | *לכל תמורה (פונקציה) <math>f\in S_n</math> נגדיר את סימן התמורה <math>sign(f)=\Pi_{i<j}\frac{f(j)-f(i)}{j-i}</math> |
| + | *תמורה נקראת חיובית או זוגית אם סימנה שווה 1, ושלילית או אי זוגית אם סימנה שווה מינוס 1. | ||
| − | === | + | |
| + | *כפליות הסימן - לכל שתי תמורות מתקיים כי <math>sign(f\circ g)=sign(f)\cdot sign(g)</math> | ||
| + | |||
| + | |||
| + | *עבור תמורת הזהות <math>I\in S_n</math> מתקיים כי<math>sign(I)=1</math> | ||
| + | |||
| + | |||
| + | <videoflash>Lmk0izbQR08</videoflash> | ||
| + | |||
| + | |||
| + | *חילוף הוא תמורה <math>(i\ j)\in S_n</math> המחליפה בין האיברים <math>i,j</math> ושולחת את שאר האיברים לעצמם. | ||
| + | |||
| + | |||
| + | *חילוף הוא תמורה שלילית (אי זוגית). | ||
| + | |||
| + | |||
| + | *מחזור הוא תמורה <math>(p_1\ p_2\ \cdots\ p_k)=(p_1\ p_2)\circ(p_2\ p_3)\circ \cdots \circ(p_{k-1}\ p_k)</math> וסימנו הוא <math>(-1)^{k-1}</math> | ||
| + | *המחזור שולח כל איבר <math>p_{i-1}</math> ל<math>p_i</math>, את <math>p_k</math> ל<math>p_1</math> ואת שאר האיברים לעצמם. | ||
| + | |||
| + | |||
| + | *כל תמורה ניתן להציג כהרכבה של מחזורים (זרים) וכך ניתן בקלות לחשב את סימנה. | ||
| + | |||
| + | |||
| + | <videoflash>oXntZnnoHfM</videoflash> | ||
| + | |||
| + | ===הגדרת הדטרמיננטה ותכונות=== | ||
| + | *עבור מטריצה ריבועית <math>A\in\mathbb{F}^{n\times n}</math> נגדיר את הדטרמיננטה: | ||
| + | **<math>det(A)=|A|=\sum_{f\in S_n}sign(f)\Pi_{i=1}^n[A]_{i,f(i)}</math> | ||
| + | |||
| + | |||
| + | <videoflash>iS2k9gdW51A</videoflash> | ||
| + | |||
| + | |||
| + | *תהי <math>A\in\mathbb{F}^{n\times n}</math> ויהיו <math>1\leq i\neq j\leq n</math> כך ש <math>R_i(A)=R_j(A)</math> אזי <math>det(A)=0</math> | ||
| + | *כלומר הדטרמיננטה של מטריצה ריבועית עם שתי שורות זהות היא אפס. | ||
| + | |||
| + | |||
| + | <videoflash>OJG5zEfaJRE</videoflash> | ||
| + | |||
| + | |||
| + | |||
| + | *תהי <math>A\in\mathbb{F}^{n\times n}</math> ותהי <math>B</math> המתקבלת מהפעלת פעולת דירוג על <math>A</math> אזי: | ||
| + | **אם פעולת הדירוג היא <math>R_i+a\cdot R_j</math> עבור <math>i\neq j</math> אזי <math>|B|=|A|</math> | ||
| + | **אם פעולת הדירוג היא <math>a\cdot R_i</math> אזי <math>|B|=a\cdot |A|</math> | ||
| + | **אם פעולת הדירוג היא <math>R_i \leftrightarrow R_j</math> עבור <math>i\neq j</math> אזי <math>|B|=-|A|</math> | ||
| + | |||
| + | |||
| + | <videoflash>QpfCfN5K8VY</videoflash> | ||
| + | |||
| + | ===חישוב הדטרמיננטה, קשר להפיכות וכפליות=== | ||
| + | |||
| + | *עבור מטריצה משולשית <math>A</math> מתקיים כי הדטרמיננטה היא מכפלת איברי האלכסון. | ||
| + | |||
| + | |||
| + | *מטריצה ריבועית היא הפיכה אם ורק אם הדטרמיננטה שלה שונה מאפס. | ||
| + | |||
| + | |||
| + | *לכל שתי מטריצות ריבועיות מתקיים כי <math>|AB|=|A|\cdot |B|</math> | ||
| + | |||
| + | |||
| + | <videoflash>kaM3ugX7izs</videoflash> | ||
| + | |||
| + | ===דטרמיננטת המשוחלפת=== | ||
| + | |||
| + | *<math>|A^t|=|A|</math> | ||
| + | |||
| + | |||
| + | *פעולות דירוג עמודות משפיעות על הדטרמיננטה בדיוק כמו פעולות דירוג שורות | ||
| + | |||
| + | |||
| + | <videoflash>i6tF0z_cXN8</videoflash> | ||
| + | |||
| + | ===נוסחת לפלס - חישוב הדטרמיננטה לפי שורה, ופיתוח הדטרמיננטה לפי עמודה=== | ||
| + | |||
| + | *<math>A_{ij}</math> היא המטריצה המתקבלת מ<math>A</math> על ידי מחיקת השורה הi והעמודה הj שלה. | ||
| + | *הדטרמיננטה <math>|A_{ij}|</math> נקראית '''מינור'''. | ||
| + | |||
| + | |||
| + | *לכל i מתקיים כי <math>det(A)=\sum_{j=1}^n (-1)^{i+j}a_{ij}|A_{ij}|</math> | ||
| + | *לכל j מתקיים כי <math>det(A)=\sum_{i=1}^n (-1)^{i+j}a_{ij}|A_{ij}|</math> | ||
| + | |||
| + | |||
| + | <videoflash>Yb1rS4lNyWk</videoflash> | ||
===מטריצה נלווית=== | ===מטריצה נלווית=== | ||
| + | |||
| + | *תהי <math>A\in\mathbb{F}^{n\times n}</math> נגדיר את המטריצה הנלווית <math>adj(A)\in\mathbb{F}^{n\times n}</math> ע"י: | ||
| + | **<math>[adj(A)]_{ij}=(-1)^{i+j}|A_{ji}|</math> | ||
| + | |||
| + | |||
| + | *מתקיים כי <math>A\cdot adj(A)=adj(A)\cdot A = |A|\cdot I</math> | ||
| + | |||
| + | |||
| + | *אם A הפיכה מתקיים כי <math>A^{-1}=\frac{1}{|A|}adj(A)</math> | ||
| + | |||
| + | |||
| + | *מתקיים כי <math>|adj(A)|=|A|^{n-1}</math> | ||
| + | |||
| + | |||
| + | <videoflash>yAnz13JHpK8</videoflash> | ||
| + | |||
| + | ===כלל קרמר=== | ||
| + | *תהי <math>A\in\mathbb{F}^{n\times n}</math> '''הפיכה''' ויהי <math>b\in\mathbb{F}^n</math> וקטור קבועים. | ||
| + | *אזי הפתרון היחיד <math>\vec{x}=(x_1,...,x_n)</math> למערכת המשוואות <math>A\vec{x}=b</math> מקיים כי: | ||
| + | *לכל i ערך המשתנה נתון ע"י <math>x_i =\frac{|A_i|}{|A|}</math> | ||
| + | *כאשר <math>A_i</math> היא המטריצה המתקבלת מ<math>A</math> על ידי החלפת העמודה ה<math>i</math> בוקטור הקבועים <math>b</math> | ||
| + | |||
| + | |||
| + | *במקרה בו יש לנו מטריצה עם שימוש נרחב בפרמטרים, קשה לדרג אותה אך קל לחשב דטרמיננטה. | ||
| + | *במקרים אלה ייתכן ויהיה רצוי למצוא את ההופכית בעזרת הנלווית, ולפתור מערכת משוואות באמצעות כלל קרמר. | ||
| + | |||
| + | |||
| + | <videoflash>1Avy8_3DzdU</videoflash> | ||
===תרגול=== | ===תרגול=== | ||
גרסה אחרונה מ־07:30, 18 ביולי 2023
תוכן עניינים
- 1 חומר עזר
- 2 סרטוני ותקציר הרצאות
- 2.1 פרק 1 - שדות
- 2.2 פרק 2- מערכות משוואות לינאריות
- 2.2.1 מבוא למטריצות ולמערכות משוואות לינאריות
- 2.2.2 הגדרת מערכת משוואות לינארית וקבוצת פתרונות
- 2.2.3 פעולות דירוג אלמנטריות
- 2.2.4 ייצוג מערכת משוואות בעזרת מטריצה
- 2.2.5 צורה מדורגת וצורה מדורגת קנונית
- 2.2.6 משתנים חופשיים ותלויים
- 2.2.7 דירוג מטריצה עם פרמטר
- 2.2.8 הוכחת קיום ויחידות צורה מדורגת קנונית
- 2.2.9 תרגול
- 2.3 פרק 3 - אלגברת מטריצות
- 2.4 פרק 4 - מרחבים וקטוריים
- 2.5 פרק 5 - העתקות לינאריות
- 2.6 פרק 6 - דטרמיננטות
חומר עזר
- סיכומי ההרצאות של ד״ר ארז שיינר, ע״י אורית חסון, קיץ 2016
- מבחנים ובחנים עם פתרונות מלאים באלגברה לינארית 1
סרטוני ותקציר הרצאות
פרק 1 - שדות
הגדרה ותכונות של שדה
- שדה הוא קבוצה
 יחד עם שתי פעולות
יחד עם שתי פעולות 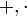 כך שמתקיימות התכונות הבאות:
כך שמתקיימות התכונות הבאות:
- סגירות: לכל
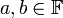 מתקיים כי
מתקיים כי 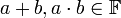
- קומוטטיביות (חילופיות): לכל
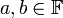 מתקיים כי
מתקיים כי  וכן
וכן 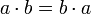
- אסוציאטיביות (קיבוץ): לכל
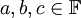 מתקיים כי
מתקיים כי 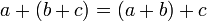 וכן
וכן 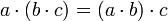
- נייטרליים: קיימים
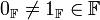 כך שלכל
כך שלכל 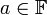 מתקיים כי
מתקיים כי 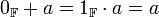
- נגדיים: לכל
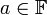 קיים נגדי
קיים נגדי 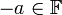 כך ש
כך ש 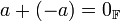
- הופכיים: לכל
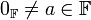 קיים הופכי
קיים הופכי 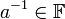 כך ש
כך ש 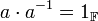
- דיסטריביוטיביות (פילוג): לכל
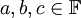 מתקיים כי
מתקיים כי 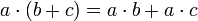
- יהי שדה
 אזי לכל
אזי לכל 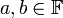 מתקיים כי
מתקיים כי 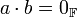 אם ורק אם
אם ורק אם 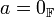 או
או 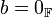
- תכונות נוספות של שדות
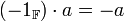
- אם
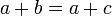 אזי
אזי 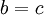
- אם
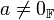 וגם
וגם 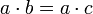 אזי
אזי 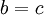
שדות סופיים
שדה המרוכבים
הגדרת המספרים המרוכבים
- נסמן
- נובע כי
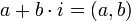
- הגדרות עבור
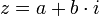
- תכונות
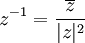 אם
אם 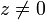
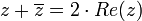
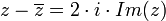
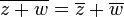
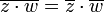
צורה קרטזית וצורה קוטבית (פולרית)
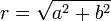
- עבור הזוית נחלק למקרים:
- אם
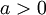 אזי
אזי 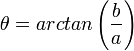
- אם
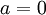 וגם
וגם 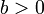 אזי
אזי 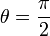
- אם
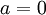 וגם
וגם 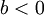 אזי
אזי 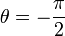
- אם
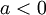 אזי
אזי 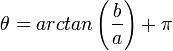
- אם
- עבור
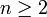 טבעי, ומספר מרוכב
טבעי, ומספר מרוכב 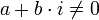 קיימים בדיוק n פתרונות למשוואה
קיימים בדיוק n פתרונות למשוואה 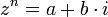
- הנוסחא למציאת כל הפתרונות השונים:
- נעביר את המספר לצורתו הקוטבית
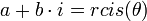
- הפתרונות הם
![z_k = \sqrt[n]{r} cis\left(\frac{\theta+2\pi k}{n}\right)](/images/math/4/0/a/40a498b3800d11f992177f92edca3fac.png) עבור
עבור 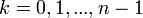
- נעביר את המספר לצורתו הקוטבית
תרגול
פרק 2- מערכות משוואות לינאריות
מבוא למטריצות ולמערכות משוואות לינאריות
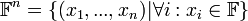 קבוצת הn-יות הסדורות.
קבוצת הn-יות הסדורות.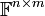 קבוצת המטריצות עם n שורות וm עמודות, ואיברים מהשדה
קבוצת המטריצות עם n שורות וm עמודות, ואיברים מהשדה 
הגדרת מערכת משוואות לינארית וקבוצת פתרונות
- מערכת משוואות לינארית היא זוג של מטריצת מקדמים
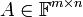 ומטריצת (וקטור) קבועים
ומטריצת (וקטור) קבועים 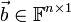 .
. - קבוצת הפתרונות למערכת המשוואות הלינארית היא קבוצת כל הn-יות המקיימות:
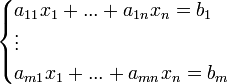
פעולות דירוג אלמנטריות
- שלושת פעולות הדירוג האלמנטריות:
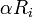 עבור
עבור 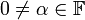 (כפל שורה במטריצה בסקלר שונה מאפס)
(כפל שורה במטריצה בסקלר שונה מאפס)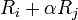 עבור
עבור 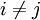 (הוספה לשורה קבוע כפול שורה אחרת)
(הוספה לשורה קבוע כפול שורה אחרת)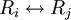 (החלפת שתי שורות במטריצה זו בזו)
(החלפת שתי שורות במטריצה זו בזו)
ייצוג מערכת משוואות בעזרת מטריצה
צורה מדורגת וצורה מדורגת קנונית
- איבר בשורה נקרא פותח/מוביל/ציר אם הוא הראשון משמאל בשורה ששונה מאפס.
- מטריצה נקראת מדורגת אם:
- אם יש שורות אפסים, כולן בתחתית.
- כל איבר פותח נמצא מימין לאיברים הפותחים בשורות מעליו.
- מטריצה נקראת מדורגת קנונית אם:
- היא מדורגת.
- כל האיברים הפותחים שווים ל1.
- בכל עמודה בה יש איבר פותח, כל האיברים מעליו שווים ל0.
משתנים חופשיים ותלויים
- משתנה נקרא תלוי אם בצורה המדורגת של המטריצה יש איבר פותח בעמודה המתאימה לו.
- כל משתנה שאינו תלוי, נקרא משתנה חופשי.
- מציאת כמות הפתרונות של מערכת משוואות לינארית:
- מדרגים את המטריצה שמייצגת את המערכת.
- אם יש שורת סתירה, אין פתרון למערכת.
- אם אין שורת סתירה, ואין משתנים חופשיים (כל המשתנים תלויים) אז יש פתרון יחיד למערכת.
- אם אין שורת סתירה, ויש משתנים חופשיים, כמות הפתרונות היא מספר האיברים בשדה בחזקת מספר המשתנים החופשיים.
- מציאת הפתרון הכללי של מערכת משוואות לינארית:
- מדרגים קנונית את המטריצה שמייצת את המערכת.
- מוודאים שאין שורת סתירה.
- בכל משתנה חופשי מציבים פרמטר.
- מבטאים את המשתנים התלויים באמצעות הפרמטרים שהצבנו.
דירוג מטריצה עם פרמטר
הוכחת קיום ויחידות צורה מדורגת קנונית
תרגול
פרק 3 - אלגברת מטריצות
חיבור מטריצות וכפל בסקלר
- תהיינה
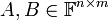 ויהי סקלר
ויהי סקלר 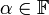
- נגדיר את
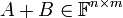 על ידי
על ידי ![[A+B]_{ij}=[A]_{ij}+[B]_{ij}](/images/math/4/8/7/4873c81b75a00720c77f1ff846f95d8c.png)
- נגדיר את
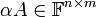 על ידי
על ידי ![[\alpha A]_{ij} = \alpha [A]_{ij}](/images/math/c/1/9/c199fb1bf5d1f5d4fdefe6f506d386fb.png)
- נגדיר את
כפל מטריצות
- תהיינה
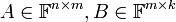
- נגדיר את המכפלה
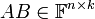 על ידי
על ידי ![[AB]_{ij}=R_i(A)C_j(B)=\sum_{p=1}^m[A]_{ip}[B]_{pj}](/images/math/0/c/9/0c92211719df4155050425d274806d9c.png)
- נגדיר את המכפלה
- הוקטור
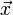 הוא פתרון למערכת המשוואות עם מטריצת המקדמים
הוא פתרון למערכת המשוואות עם מטריצת המקדמים  ווקטור הקבועים
ווקטור הקבועים 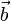 אם ורק אם
אם ורק אם 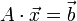
שיטות לחישוב כפל מטריצות
- חישוב הכפל לפי עמודות
- חישוב הכפל לפי שורות
תכונות של אלגברת מטריצות
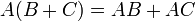 וכן
וכן 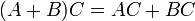
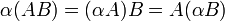
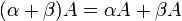 וכן
וכן 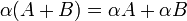
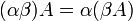
- מטריצת היחידה
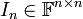 מוגדרת על ידי
מוגדרת על ידי ![[I_n]_{ij}=\begin{cases}1 & i=j\\ 0 & i\neq j\end{cases}](/images/math/2/2/c/22cb810e33313570df86e769aa4a3e1e.png)
- לכל
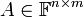 מתקיים כי
מתקיים כי 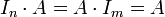
- לכל שלוש מטריצות מתקיים חוק הקיבוץ (אסוציאטיביות)
פתרון כללי למערכת משוואות לא הומוגנית
- פתרון פרטי למערכת הלא הומוגנית + פתרון כללי למערכת ההומוגנית = פתרון כללי למערכת הלא הומוגנית
שחלוף
- עבור
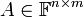 נגדיר את המטריצה המשוחלפת
נגדיר את המטריצה המשוחלפת 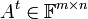 על ידי
על ידי ![[A^t]_{ij}=[A]_{ji}](/images/math/2/0/9/209f15d7650597a91ab1f9ed77aa8fab.png)
עקבה
- העקבה (trace) של מטריצה ריבועית היא סכום איברי האלכסון:
- עבור
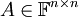 נגדיר
נגדיר ![tr(A)=\sum_{i=1}^n[A]_{ii}](/images/math/0/f/9/0f924e7028154d1f0969dd71c55a7a7e.png)
- עבור
- תכונות העקבה:
- דוגמא: לא קיימות מטריצות ממשיות
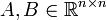 כך ש
כך ש 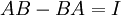
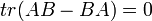 אך
אך 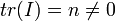
תרגול
מטריצות הפיכות ומטריצות הופכיות
- מטריצה
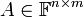 נקראת הפיכה אם קיימות מטריצות
נקראת הפיכה אם קיימות מטריצות 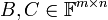 כך ש
כך ש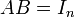 וכן
וכן 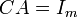
- אם מטריצה היא הפיכה, קיימת מטריצה יחידה שנסמנה
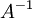 ונקרא לה ההופכית של
ונקרא לה ההופכית של  המקיימת
המקיימת 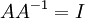 . כמו כן היא המטריצה היחידה המקיימת
. כמו כן היא המטריצה היחידה המקיימת 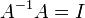 .
.
- תהי
 הפיכה, אזי למערכת המשוואות
הפיכה, אזי למערכת המשוואות 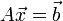 יש פתרון יחיד, והוא
יש פתרון יחיד, והוא 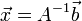
- תהיינה
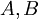 הפיכות מעל אותו שדה כך שהכפל
הפיכות מעל אותו שדה כך שהכפל 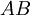 מוגדר, אזי
מוגדר, אזי 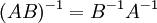
- תהי
 הפיכה אזי
הפיכה אזי 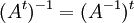
- תהי
 הפיכה אזי
הפיכה אזי 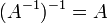
- תהי
 הפיכה ויהי סקלר
הפיכה ויהי סקלר 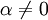 אזי
אזי 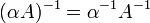
מטריצות פעולה
- תהי
 פונקצית פעולה המבצעת פעולת דירוג אלמנטרית מסוימת.
פונקצית פעולה המבצעת פעולת דירוג אלמנטרית מסוימת. - לכל
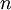 נגדיר את מטריצת הפעולה
נגדיר את מטריצת הפעולה 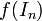 .
. - לכל מטריצה
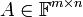 מתקיים כי
מתקיים כי 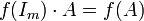
- מטריצת הפעולה היא הפיכה.
- לכל מטריצה
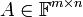 קיימת מטריצה הפיכה
קיימת מטריצה הפיכה 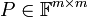 כך ש
כך ש 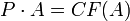
בדיקת הופכיות ומציאת ההופכית
- מטריצה מחלקת אפס אינה הפיכה. כלומר, אם
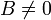 אך
אך 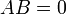 או
או 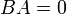 אזי
אזי  אינה הפיכה
אינה הפיכה - אם ב
 השורה הi היא שורת אפסים, אזי לכל
השורה הi היא שורת אפסים, אזי לכל  כך שהכפל מוגדר, השורה הi ב
כך שהכפל מוגדר, השורה הi ב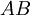 היא שורת אפסים.
היא שורת אפסים.
- ב
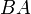 לא חייבת להיות שורת אפסים, לעומת זאת.
לא חייבת להיות שורת אפסים, לעומת זאת.
- ב
- מטריצה עם שורת אפסים אינה הפיכה.
- מטריצה הפיכה חייבת להיות ריבועית.
- מטריצה
 היא הפיכה אם ורק אם
היא הפיכה אם ורק אם 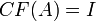
- אם
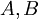 ריבועיות כך ש
ריבועיות כך ש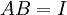 אזי
אזי 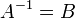
- תהיינה
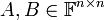 ריבועיות אזי
ריבועיות אזי 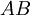 הפיכה אם ורק אם
הפיכה אם ורק אם 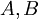 הפיכות שתיהן
הפיכות שתיהן
- דוגמא לשתי מטריצות לא הפיכות שמכפלתן הפיכה (זה לא סותר את המשפטים לעיל כיוון שהמטריצות אינן ריבועיות).
אלגוריתם לבדיקת הפיכות ומציאת ההופכית
- תהי מטריצה ריבועית
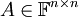
- נדרג את מטריצת הבלוקים
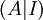 קנונית.
קנונית. - אם בשלב כלשהו נגלה שבצורה המדורגת של
 יש שורת אפסים, אזי היא אינה הפיכה.
יש שורת אפסים, אזי היא אינה הפיכה. - אחרת, הצורה הקנונית של
 היא
היא 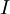 ולכן היא הפיכה.
ולכן היא הפיכה. - הגענו למטריצת הבלוקים
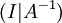 .
.
תרגול
תרגול בנושא מטריצות הפיכות ומטריצות פעולה
פרק 4 - מרחבים וקטוריים
הגדרה ותכונות של מרחבים וקטוריים
- מרחב וקטורי
 מעל שדה
מעל שדה  הוא קבוצת איברים (הנקראים וקטורים) יחד עם פעולת חיבור וכפל בסקלר, כך שמתקיימות התכונות הבאות:
הוא קבוצת איברים (הנקראים וקטורים) יחד עם פעולת חיבור וכפל בסקלר, כך שמתקיימות התכונות הבאות:
- סגירות:
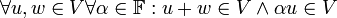
- חילופיות:
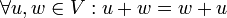
- אסוציאטיביות (קיבוץ):
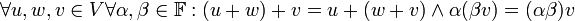
- נייטרלי לחיבור:
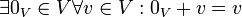
- נגדיים:
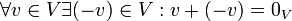
- נייטרלי לכפל בסקלר:
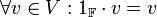
- דיסטריביוטיביות (פילוג):
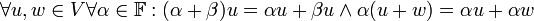
- יהי
 מ"ו מעל שדה
מ"ו מעל שדה  ויהיו
ויהיו 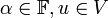 אזי:
אזי:
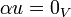 אם ורק אם
אם ורק אם 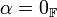 או
או 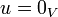
- כמו כן,
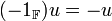
תתי מרחבים
- יהי
 מ"ו מעל שדה
מ"ו מעל שדה  , ותהי
, ותהי 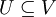 תת קבוצה של וקטורים.
תת קבוצה של וקטורים. - אזי
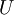 נקרא תת מרחב של
נקרא תת מרחב של  אם הוא מהווה מרחב וקטורי יחד עם פעולת החיבור והכפל בסקלר של
אם הוא מהווה מרחב וקטורי יחד עם פעולת החיבור והכפל בסקלר של  .
.
- יהי
 מ"ו מעל שדה
מ"ו מעל שדה  , ותהי
, ותהי 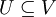 תת קבוצה של וקטורים.
תת קבוצה של וקטורים. - אזי
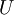 תת מרחב אם ורק אם מתקיימים שני התנאים הבאים:
תת מרחב אם ורק אם מתקיימים שני התנאים הבאים:
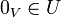
- לכל
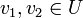 ולכל
ולכל 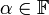 מתקיים כי
מתקיים כי 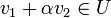
- תהי
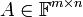 אזי קבוצת הפתרונות של המערכת ההומוגנית
אזי קבוצת הפתרונות של המערכת ההומוגנית 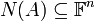 הינה תת מרחב וקטורי.
הינה תת מרחב וקטורי.
- קבוצת הפתרונות של מערכת לא הומוגנית אינה תת מרחב וקטורי כיוון שהיא אינה מכילה את וקטור האפס.
- אוסף המטריצות הסימטריות מהווה תת מרחב של אוסף המטריצות הריבועיות.
- אוסף הפולינומים שמתאפסים בנקודה מסויימת, מהווה תת מרחב של אוסף הפולינומים.
חיתוך, סכום, וסכום ישר של תתי מרחבים
- יהי
 מ"ו מעל שדה
מ"ו מעל שדה  , ויהיו
, ויהיו 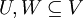 , תתי מרחב.
, תתי מרחב.
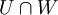 הינו תת מרחב של
הינו תת מרחב של  .
.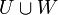 תת מרחב של
תת מרחב של  אם ורק אם
אם ורק אם 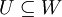 או
או 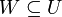 .
.
- יהי
 מ"ו מעל שדה
מ"ו מעל שדה  , ויהיו
, ויהיו 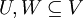 , תתי מרחב.
, תתי מרחב. - נגדיר את סכום תתי המרחבים:
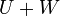 הינו תת המרחב הקטן ביותר שמכיל את
הינו תת המרחב הקטן ביותר שמכיל את 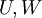 . כלומר סכום תתי מרחבים הוא תת מרחב וגם:
. כלומר סכום תתי מרחבים הוא תת מרחב וגם:
- לכל תת מרחב
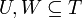 מתקיים כי
מתקיים כי 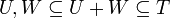
- לכל תת מרחב
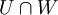 הינו תת המרחב הגדול ביותר שמוכל ב
הינו תת המרחב הגדול ביותר שמוכל ב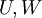 . כלומר חיתוך תתי מרחבים הוא תת מרחב וגם:
. כלומר חיתוך תתי מרחבים הוא תת מרחב וגם:
- לכל תת מרחב
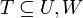 מתקיים כי
מתקיים כי 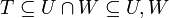
- לכל תת מרחב
- דוגמא:
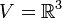
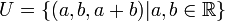
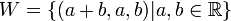
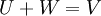
- ניתן להציג וקטור בשתי דרכים שונות כסכום של רכיב מU ועוד רכיב מW:
- סכום ישר:
- יהי V מ"ו ויהיו U,W תתי מרחב. אומרים ש
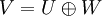 אם מתקיימים שני התנאים הבאים:
אם מתקיימים שני התנאים הבאים:
- משפט:
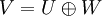 אם ורק אם לכל וקטור
אם ורק אם לכל וקטור 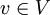 קיימת הצגה יחידה
קיימת הצגה יחידה 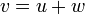 כסכום של רכיבים מU ומW.
כסכום של רכיבים מU ומW.
- כלומר בדוגמא לעיל, הסכום אינו ישר, כיוון שהצגנו וקטור אחד בשתי דרכים שונות.
תרגול
פרישה ותלות לינארית
- יהי
 מ"ו מעל שדה
מ"ו מעל שדה  ותהי
ותהי 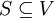 .
.
- וקטור
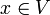 נקרא צירוף לינארי של הקבוצה
נקרא צירוף לינארי של הקבוצה  אם
אם 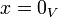 או קיימים וקטורים בקבוצה
או קיימים וקטורים בקבוצה 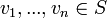 וסקלרים מהשדה
וסקלרים מהשדה 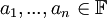 כך ש
כך ש 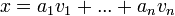
- וקטור
- כלומר, ניתן "ליצור" את x בעזרת פעולות המרחב הוקטורי על הקבוצה S (או שx=0)
- אוסף כל הוקטורים במרחב שהם צירופים לינאריים של S נקרא
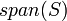 .
.
- טענה: יהי V מ"ו ותהי
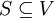 אזי
אזי 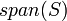 הוא תת המרחב הקטן ביותר שמכיל את
הוא תת המרחב הקטן ביותר שמכיל את  . כלומר:
. כלומר:
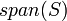 תת מרחב וקטורי
תת מרחב וקטורי- לכל תת מרחב
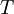 כך ש
כך ש 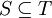 מתקיים כי
מתקיים כי 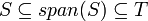
- יהי
 מ"ו מעל שדה
מ"ו מעל שדה  , ותהי n-ית וקטורים
, ותהי n-ית וקטורים 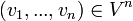 . אומרים שהוקטורים
. אומרים שהוקטורים 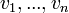 (לאו דווקא שונים) תלויים לינארית או ת"ל בקיצור, אם קיימים סקלרים
(לאו דווקא שונים) תלויים לינארית או ת"ל בקיצור, אם קיימים סקלרים 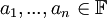 לא כולם אפס כך שהצירוף הלינארי מתאפס
לא כולם אפס כך שהצירוף הלינארי מתאפס 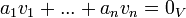 .
. - אם הוקטורים אינם תלויים לינארית, אומרים שהם בלתי תלויים לינארית או בת"ל בקיצור.
- קבוצה
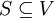 נקראת תלוייה לינארית אם קיימים
נקראת תלוייה לינארית אם קיימים 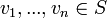 וקטורים שונים שתלויים לינארית.
וקטורים שונים שתלויים לינארית.
- יהיו
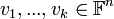 .
. - הם בת"ל אם ורק אם הפתרון היחיד למשוואה
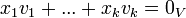 הוא שכל הסקלרים הם אפסים.
הוא שכל הסקלרים הם אפסים.
- בעזרת חישוב הכפל לפי עמודות
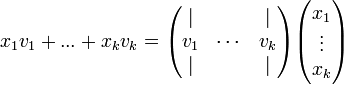
- בעזרת חישוב הכפל לפי עמודות
- לכן אם נשים את הוקטורים בעמודות מטריצה A, נקבל שהם בת"ל אם ורק אם למערכת המשוואות ההומוגנית יש פתרון יחיד כלומר
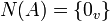
- באופן דומה, אלגוריתם לקבוע האם
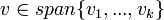 :
:
- נשים את הוקטורים
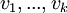 בעמודות מטריצה A, ונשים את v בעמודה כוקטור הקבועים.
בעמודות מטריצה A, ונשים את v בעמודה כוקטור הקבועים. - הוקטור שייך למרחב אם ורק אם למערכת הלא הומוגנית יש פתרון.
- נשים את הוקטורים
בסיס ומימד
- לֶמת ההחלפה של שטייניץ
- יהי
 מ"ו ותהיינה
מ"ו ותהיינה 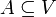 בת"ל וכן
בת"ל וכן 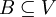 פורשת (כלומר
פורשת (כלומר 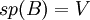 ).
). - אזי לכל
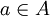 קיים
קיים 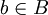 כך ש
כך ש 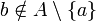 וגם הקבוצה
וגם הקבוצה 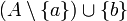 בת"ל.
בת"ל.
- יהי
 מ"ו ותהי
מ"ו ותהי 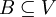 קבוצה פורשת (כלומר
קבוצה פורשת (כלומר 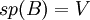 ) כך ש
) כך ש 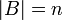 (כלומר יש בה n וקטורים).
(כלומר יש בה n וקטורים). - תהי בנוסף
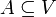 קבוצה בת"ל, אזי
קבוצה בת"ל, אזי 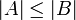 (כלומר כמות הוקטורים בקבוצה בת"ל קטנה או שווה לכמות הוקטורים בקבוצה פורשת).
(כלומר כמות הוקטורים בקבוצה בת"ל קטנה או שווה לכמות הוקטורים בקבוצה פורשת).
- הגדרת בסיס:
- יהי
 מ"ו ותהי
מ"ו ותהי 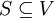 קבוצת וקטורים.
קבוצת וקטורים. - אם
 בת"ל וגם פורשת את כל המרחב (כלומר
בת"ל וגם פורשת את כל המרחב (כלומר 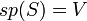 ) אזי היא נקראת בסיס למרחב
) אזי היא נקראת בסיס למרחב  .
.
- יהי
 מ"ו נוצר סופית (כלומר קיימת קבוצה סופית
מ"ו נוצר סופית (כלומר קיימת קבוצה סופית 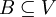 שפורשת את כל המרחב
שפורשת את כל המרחב 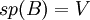 ).
). - אזי קיים לו בסיס סופי.
- כמו כן, בכל שני בסיסים במרחב יש בדיוק את אותה כמות הוקטורים.
- כמות הוקטורים בבסיס מוגדרת להיות המימד של המרחב. כלומר בהנתן בסיס B מגדירים
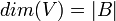 .
.
- כל תת מרחב של מרחב נוצר סופית גם נוצר סופית, ולכן גם עבורו מוגדר מימד.
העשרה
- לכל מרחב וקטורי יש בסיס.
- ניקח שרשרת מקסימלית של קבוצות בת"ל M.
- נגדיר את האיחוד הכללי של M להיות B.
- B בת"ל, כי אם יש בה וקטורים תלויים, הם הגיעו מאחד הקבוצות (בשרשרת כל מספר סופי של קבוצות מוכלות באחת מהן)
- B פורשת, אחרת היה ניתן להגדיל אותה באמצעות וקטור שאינו נפרש על ידה, היינו מקבלים קבוצה בת"ל חדשה שניתן להוסיף לשרשרת המקסימלית, בסתירה.
משפט השלישי חינם
- יהי
 מ"ו ממימד
מ"ו ממימד 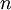 ותהי
ותהי 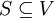 .
. - אזי אם שניים מבין התנאים הבאים מתקיימים, גם השלישי מתקיים ו
 מהווה בסיס למרחב
מהווה בסיס למרחב  .
.
 בת"ל
בת"ל פורשת (כלומר
פורשת (כלומר 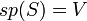 )
)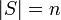 (כלומר כמות הוקטורים ב
(כלומר כמות הוקטורים ב שווה למימד)
שווה למימד)
- יהי
 מ"ו נוצר סופית, ויהי
מ"ו נוצר סופית, ויהי 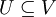 תת מרחב.
תת מרחב. - אם
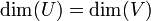 אזי
אזי 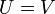
תרגול
משפט המימדים
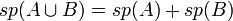
תרגול
הצגה פרמטרית ואלגברית
שלושת מרחבי המטריצה ומציאת בסיסים
- תהי
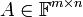
- על מנת למצוא בסיס לחיתוך בין תתי מרחבים, נציג את שניהם בצורה אלגברית והחיתוך הוא אוסף הפתרונות של המשוואות משתי המערכות.
- על מנת למצוא בסיס לסכום תתי מרחבים, נציג את שניהם בצורה פרמטרית והסכום נפרש ע"י איחוד הקבוצות הפורשות.
- ניתן להשלים כל קבוצה בת"ל לבסיס.
- לוקחים את הקבוצה הבת"ל, מוסיפים לה בסיס כלשהו, מדרגים בעמודות ומוחקים את הוקטורים המיותרים.
תרגול
דרגה של מטריצה
- בכל צורה מדורגת של A, האיברים הפותחים נמצאים באותן העמודות.
- כל הגדלים הבאים שווים:
- דרגה של מטריצה
- מימד מרחב העמודות
- מימד מרחב השורות
- מספר השורות השונות מאפס בצורה המדורגת
- מספר המשתנים התלויים במערכת ההומוגנית
- כמו כן, מימד מרחב האפס שווה למספר המשתנים החופשיים.
- ביחד מקבלים את משפט הדרגה (שנוכיח במדויק בהמשך): דרגת המטריצה ועוד מימד מרחב האפס שווה לכמות עמודות המטריצה (מספר המשתנים).
פרק 5 - העתקות לינאריות
העתקות, הרכבת העתקות, הפיכות העתקות
- יהיו
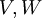 מ"ו מעל אותו שדה
מ"ו מעל אותו שדה  .
. - פונקציה
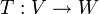 נקראת העתקה לינארית אם לכל
נקראת העתקה לינארית אם לכל 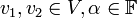 היא מקיימת:
היא מקיימת:
- שימו לב לסימון
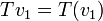
פעולות בין העתקות לינאריות
- הרכבת העתקות לינאריות היא העתקה לינארית
- סכום וכפל בסקלר של העתקות לינאריות היא העתקה לינארית
- הפונקציה ההופכית של העתקה לינארית הפיכה היא העתקה לינארית
גרעין ותמונה
- תהי
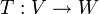 העתקה לינארית
העתקה לינארית
- הגרעין
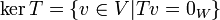 הוא תת מרחב של התחום
הוא תת מרחב של התחום 
- התמונה
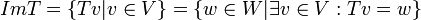 היא תת מרחב של הטווח
היא תת מרחב של הטווח 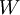
- הגרעין
- ההעתקה
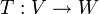 חח"ע אם ורק אם
חח"ע אם ורק אם 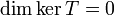
- ההעתקה
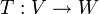 על אם ורק אם
על אם ורק אם 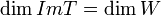
משפט הדרגה להעתקות לינאריות ולמטריצות
- תהי העתקה לינארית
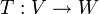 ויהי
ויהי 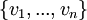 בסיס לV.
בסיס לV. - אזי
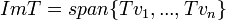
- תהי
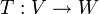 העתקה לינארית אזי
העתקה לינארית אזי 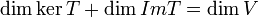
- תהי
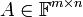 אזי
אזי 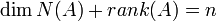
- תהי
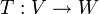 העתקה לינארית בין מרחבים וקטוריים נוצרים סופית.
העתקה לינארית בין מרחבים וקטוריים נוצרים סופית.
- אם T חח"ע אז
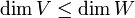
- אם T על אזי
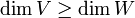
- אם
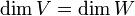 אזי T חח"ע אם"ם T על.
אזי T חח"ע אם"ם T על.
- אם T חח"ע אז
- העתקה לינארית נקראת גם הומומורפיזם. העתקה לינארית הפיכה נקראת איזומורפיזם.
- מרחבים וקטוריים נקראים איזומורפייים זה לזה, אם קיים איזומורפיזם בינהם (זהו יחס שקילות).
- מרחבים וקטוריים נוצרים סופית איזומורפיים זה לזה, אם ורק אם המימדים שלהם שווים.
תרגול
יחידות הצגה לפי בסיס ומשפט ההגדרה
- יהי V מ"ו ויהי
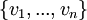 בסיס סדור לV.
בסיס סדור לV. - אזי לכל
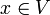 קיימת הצגה יחידה כצירוף לינארי של איברי הבסיס:
קיימת הצגה יחידה כצירוף לינארי של איברי הבסיס:
- יהיו V,W מ"ו מעל אותו שדה, ויהי
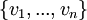 בסיס סדור לV.
בסיס סדור לV. - תהיינה סדרת וקטורים
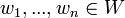 לאו דווקא שונים.
לאו דווקא שונים. - אזי קיימת העתקה לינארית יחידה
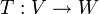 המקיימת:
המקיימת:
- לכל i מתקיים כי
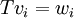
- לכל i מתקיים כי
מטריצה מייצגת העתקה
קואורדינטות
- יהי V מ"ו ויהי
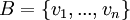 בסיס סדור לV.
בסיס סדור לV. - לכל
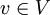 נגדיר את וקטור הקואורדינטות לפי B להיות הסקלים מההצגה היחידה:
נגדיר את וקטור הקואורדינטות לפי B להיות הסקלים מההצגה היחידה:
![[v]_B=\begin{pmatrix}\alpha_1 \\ \vdots \\ \alpha_n\end{pmatrix}](/images/math/f/7/7/f770f90eab54560de5fbca6307a98d72.png) אם ורק אם
אם ורק אם 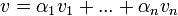
- מה עושים עם הקואורדינטות? כופלים באיברי הבסיס!
- נגדיר פונקציה
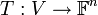 ע"י
ע"י ![Tv=[v]_B](/images/math/0/7/0/07057ec189d16374c52d67414b4eab25.png) , אזי T היא איזומורפיזם. לכן
, אזי T היא איזומורפיזם. לכן
![[a_1u_1+...+a_ku_k]_B=a_1[u_1]_B+...+a_k[u_k]_B](/images/math/8/f/4/8f433912f785d66ddb795e5f40c67508.png)
- הסדרה
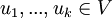 בת"ל אם ורק אם הסדרה
בת"ל אם ורק אם הסדרה ![[u_1]_B,...,[u_k]_B](/images/math/e/b/4/eb4b5b4e735834a276365d7282070e08.png) בת"ל
בת"ל 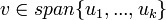 אם ורק אם
אם ורק אם ![[v]_B\in span \{[u_1]_B,...,[u_k]_B\}](/images/math/8/7/2/872d6ba88b8319426cfc29120a379ad9.png)
משפט קיום ויחידות
- יהיו
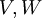 מ"ו מעל אותו שדה
מ"ו מעל אותו שדה  .
. - נניח V ממימד n וB בסיס סדור שלו.
- נניח W ממימד m וC בסיס סדור שלו.
- תהי
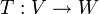 העתקה לינארית.
העתקה לינארית. - אזי:
- קיימת מטריצה יחידה
![[T]_C^B\in\mathbb{F}^{m\times n}](/images/math/9/e/2/9e2bea49ec453050f6289e3d699fc3a2.png) המקיימת:
המקיימת: - לכל
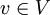 מתקיים כי
מתקיים כי ![[T]_C^B[v]_B=[Tv]_C](/images/math/f/5/5/f55b0230a9d227de79004abb3c264b69.png)
- קיימת מטריצה יחידה
- על מנת למצוא את המטריצה המייצגת:
- נפעיל את ההעתקה על איברי הבסיס של התחום.
- נמצא את הקואורדינטות של תמונות איברי בסיס התחום לפי בסיס הטווח.
- נשים את וקטורי הקואורדינטות שמצאנו בעמודות ונקבל את המטריצה המייצגת.
המטריצה המייצגת את ההעתקה ההופכית
- יהיו
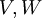 מ"ו ממימד סופי מעל השדה
מ"ו ממימד סופי מעל השדה  עם בסיסים
עם בסיסים 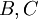 בהתאמה.
בהתאמה. - תהי
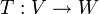 העתקה לינארית, ויהי סקלר
העתקה לינארית, ויהי סקלר 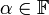
- אזי
![[T+S]^B_C=[T]^B_C+[S]^B_C](/images/math/8/3/b/83bd2ff2a8737b59b6ca35880ac60f46.png)
![[\alpha T]^B_C=\alpha[T]^B_C](/images/math/2/4/f/24f6ec08d7b11a0c49e3a9052eaa462e.png)
![[S\circ T]_D^B=[S]^C_D[T]_C^B](/images/math/e/1/0/e10efe743e4875a564ec343ecbdcb2bf.png)
- ההעתקה T הפיכה אם ורק אם המטריצה המייצגת
![[T]^B_C](/images/math/5/d/b/5dbb19b8663cf8506d72d49add1f4957.png) הפיכה
הפיכה
- אם ההעתקה הפיכה, מתקיים כי
![[T^{-1}]^C_B = \left([T]^B_C\right)^{-1}](/images/math/3/a/b/3ab5629216676438db199608b2463efc.png)
- אם ההעתקה הפיכה, מתקיים כי
מטריצות מעבר בין בסיסים
שלוש צורות הצגת ההעתקה
- ניתן להציג העתקה לינארית בשלוש דרכים:
- נוסחא מפורשת
- לפי בסיס
- בעזרת מטריצה מייצגת
תרגול
- תרגול המכיל קואורדינטות ומטריצות מעבר בין בסיסים
- תרגול בנושא מטריצות מייצגות העתקות
- תרגול נוסף בנושא העתקות
פרק 6 - דטרמיננטות
תמורות
- נגדיר את אוסף התמורות
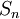 להיות קבוצת כל הפונקציות ההפיכות מהקבוצה
להיות קבוצת כל הפונקציות ההפיכות מהקבוצה 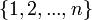 לעצמה.
לעצמה.
- לכל תמורה (פונקציה)
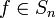 נגדיר את סימן התמורה
נגדיר את סימן התמורה 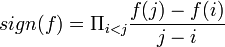
- תמורה נקראת חיובית או זוגית אם סימנה שווה 1, ושלילית או אי זוגית אם סימנה שווה מינוס 1.
- כפליות הסימן - לכל שתי תמורות מתקיים כי
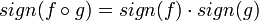
- עבור תמורת הזהות
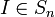 מתקיים כי
מתקיים כי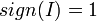
- חילוף הוא תמורה
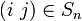 המחליפה בין האיברים
המחליפה בין האיברים 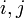 ושולחת את שאר האיברים לעצמם.
ושולחת את שאר האיברים לעצמם.
- חילוף הוא תמורה שלילית (אי זוגית).
- מחזור הוא תמורה
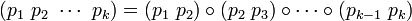 וסימנו הוא
וסימנו הוא 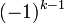
- המחזור שולח כל איבר
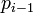 ל
ל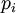 , את
, את 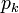 ל
ל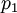 ואת שאר האיברים לעצמם.
ואת שאר האיברים לעצמם.
- כל תמורה ניתן להציג כהרכבה של מחזורים (זרים) וכך ניתן בקלות לחשב את סימנה.
הגדרת הדטרמיננטה ותכונות
- עבור מטריצה ריבועית
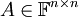 נגדיר את הדטרמיננטה:
נגדיר את הדטרמיננטה:
- תהי
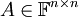 ויהיו
ויהיו 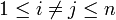 כך ש
כך ש 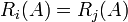 אזי
אזי 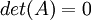
- כלומר הדטרמיננטה של מטריצה ריבועית עם שתי שורות זהות היא אפס.
- תהי
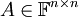 ותהי
ותהי  המתקבלת מהפעלת פעולת דירוג על
המתקבלת מהפעלת פעולת דירוג על  אזי:
אזי:
- אם פעולת הדירוג היא
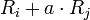 עבור
עבור 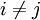 אזי
אזי 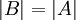
- אם פעולת הדירוג היא
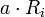 אזי
אזי 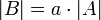
- אם פעולת הדירוג היא
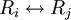 עבור
עבור 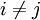 אזי
אזי 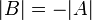
- אם פעולת הדירוג היא
חישוב הדטרמיננטה, קשר להפיכות וכפליות
- עבור מטריצה משולשית
 מתקיים כי הדטרמיננטה היא מכפלת איברי האלכסון.
מתקיים כי הדטרמיננטה היא מכפלת איברי האלכסון.
- מטריצה ריבועית היא הפיכה אם ורק אם הדטרמיננטה שלה שונה מאפס.
- לכל שתי מטריצות ריבועיות מתקיים כי
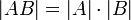
דטרמיננטת המשוחלפת
- פעולות דירוג עמודות משפיעות על הדטרמיננטה בדיוק כמו פעולות דירוג שורות
נוסחת לפלס - חישוב הדטרמיננטה לפי שורה, ופיתוח הדטרמיננטה לפי עמודה
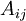 היא המטריצה המתקבלת מ
היא המטריצה המתקבלת מ על ידי מחיקת השורה הi והעמודה הj שלה.
על ידי מחיקת השורה הi והעמודה הj שלה.- הדטרמיננטה
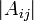 נקראית מינור.
נקראית מינור.
- לכל i מתקיים כי
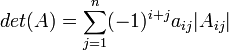
- לכל j מתקיים כי
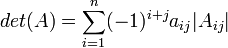
מטריצה נלווית
- תהי
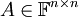 נגדיר את המטריצה הנלווית
נגדיר את המטריצה הנלווית 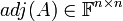 ע"י:
ע"י:
- מתקיים כי
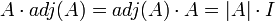
- אם A הפיכה מתקיים כי
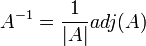
- מתקיים כי
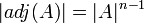
כלל קרמר
- תהי
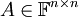 הפיכה ויהי
הפיכה ויהי 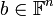 וקטור קבועים.
וקטור קבועים. - אזי הפתרון היחיד
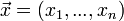 למערכת המשוואות
למערכת המשוואות 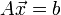 מקיים כי:
מקיים כי: - לכל i ערך המשתנה נתון ע"י
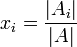
- כאשר
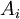 היא המטריצה המתקבלת מ
היא המטריצה המתקבלת מ על ידי החלפת העמודה ה
על ידי החלפת העמודה ה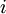 בוקטור הקבועים
בוקטור הקבועים 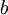
- במקרה בו יש לנו מטריצה עם שימוש נרחב בפרמטרים, קשה לדרג אותה אך קל לחשב דטרמיננטה.
- במקרים אלה ייתכן ויהיה רצוי למצוא את ההופכית בעזרת הנלווית, ולפתור מערכת משוואות באמצעות כלל קרמר.
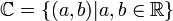
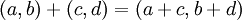
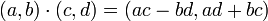
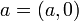
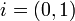
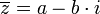
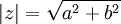
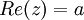
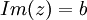
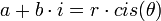
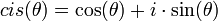
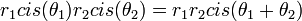
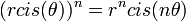
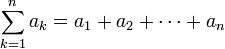
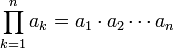
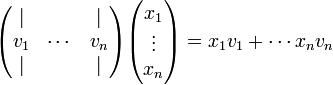
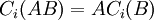
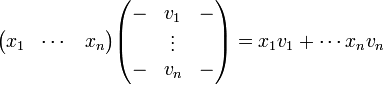
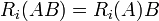
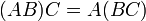
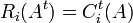
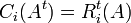
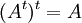
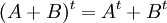
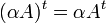
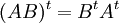
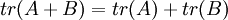
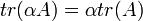
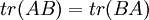
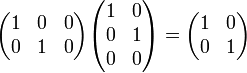
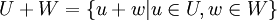
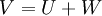
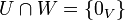
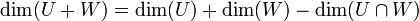
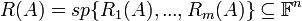
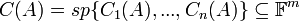
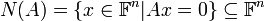
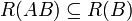
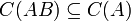
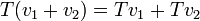
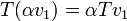
![[T]_C^B= \begin{pmatrix}| & & | \\ \left[T v_1 \right]_C & \cdots & \left[ T v_n \right]_C \\ | & & | \end{pmatrix} \in \mathbb{F}^{m\times n}](/images/math/7/1/8/718b7a3ba4803acbc834f0cbed18416f.png)
![[I]_{C_2}^{C_1}[T]_{C_1}^{B_1}[I]_{B_1}^{B_2}=[T]_{C_2}^{B_2}](/images/math/c/a/9/ca98ceebeaa41026b3a3bb362338f208.png)
![\left([I]_C^B\right)^{-1}=[I]_B^C](/images/math/c/e/4/ce483c71a2f71ddb7d585f9494aeea81.png)
![det(A)=|A|=\sum_{f\in S_n}sign(f)\Pi_{i=1}^n[A]_{i,f(i)}](/images/math/1/5/e/15e771f61db1c6250fbd8686906fd987.png)
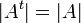
![[adj(A)]_{ij}=(-1)^{i+j}|A_{ji}|](/images/math/2/c/b/2cb7b3ec3ba825fdabf1020b67b4254a.png)