הבדלים בין גרסאות בדף "שיחה:88-132 סמסטר א' תשעא"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏תשובה)
(←‏שאלה קלה מדי?)
 
(751 גרסאות ביניים של יותר מ־100 משתמשים אינן מוצגות)
שורה 10: שורה 10:
 
*[[שיחה:88-132 סמסטר א' תשעא/ ארכיון 6| ארכיון 6]]
 
*[[שיחה:88-132 סמסטר א' תשעא/ ארכיון 6| ארכיון 6]]
 
*[[שיחה:88-132 סמסטר א' תשעא/ ארכיון 7| ארכיון 7]]
 
*[[שיחה:88-132 סמסטר א' תשעא/ ארכיון 7| ארכיון 7]]
 +
*[[שיחה:88-132 סמסטר א' תשעא/ ארכיון 8| ארכיון 8]]
 +
*[[שיחה:88-132 סמסטר א' תשעא/ ארכיון 9| ארכיון 9]]
 +
*[[שיחה:88-132 סמסטר א' תשעא/ ארכיון 10| ארכיון 10]]
 +
*[[שיחה:88-132 סמסטר א' תשעא/ ארכיון 11| ארכיון 11]]
 +
*[[שיחה:88-132 סמסטר א' תשעא/ ארכיון 12| ארכיון 12]]
 +
*[[שיחה:88-132 סמסטר א' תשעא/ ארכיון 13| ארכיון 13]]
 +
*[[שיחה:88-132 סמסטר א' תשעא/ ארכיון 14| ארכיון 14]]
 +
*[[שיחה:88-132 סמסטר א' תשעא/ ארכיון 15| ארכיון 15]]
 +
  
 
=שאלות=
 
=שאלות=
  
−
== בקשר לשאלה 4 בתרגיל 6 ==
+
== הערה בקשר למבחן ביום שני ==
−
בשאלה אנו דרושים למצוא סכומים של סדרות. האם אנו צריכים להוכיח קודם כי קיים גבול ורק אחר כך למצוא אותו, או אפשר ישר למצוא אותו?
+
 
 +
אני תלמיד של מיכאל שיין ולא היה לנו תרגול אחד על חתכי דדקינד בכל הסמסטר ואני בספק אם מישהו יודע איך לפתור את התרגילים בנושא חתכי דדקינד.
 +
 
 +
אשמח אם תתחשבו בנו.
 +
 
 +
:מצטרפת. לא היו שיעורי בית בנושא, בהרצאה לא פתרנו תרגילים, ואין במיזלר. אשמח אם תענו לי למטה על השאלה לגבי חתכי דדקינד.
 +
 
 +
 
 +
מצטרף גם.. אין לנו מושג איך לגשת לתרגילים האלו כי אף פעם לא הראנו לנו איך לפתור תרגילים כאלה.. אפשר להעלות חומר ללימוד או לפחות פתרון לתרגיל שאדווארד העלה לאתר:
 +
http://sites.google.com/site/eduardkontorovich/
 +
 
 +
אני חושב שכמעט אף אחד בקבוצה לא יודע לפתור תרגילים כאלה..
 +
::ואם מישהו יודע (ולא נראה לי), אז הוא בטוח למד ממקור נוסף שאני לא מכירה.
 +
 
 +
http://dl.dropbox.com/u/2237179/infi1dedekind.pdf
 +
 
 +
== שאלה בקשר למבחן ביום שני ==
 +
 
 +
מישהו יכול בבקשה לפרט אילו שאלות עלולות להופיע במבחן באינפי 1 ביום שני? יופיעו שאלות חישוביות?
 
תודה.
 
תודה.
 +
:תלוי באיזו קבוצה אתה. אם אתה אצל התיכוניסטים, מבנה המבחן הוא כדלקמן:
 +
:יש שש שאלות ואין בחירה ביניהן, סה"כ זמן המבחן שעתיים וחצי. כל שאלה 18 נקודות = סה"כ 108 נקודות.
 +
:תהיה שאלה על סדרות, על טורים, על פונקציות (גבולות וכדומה), רציפות/רציפות במ"ש, נגזרות ויישמון של נזגרות (טיילור, לופיטל וכו...). עבור תלמידיו של ד"ר שיין - יהיו חתכי דדקינד במקום ישומי הנגזרות.
 +
:כל מה שנכתב כאן נאמר על ידי ד"ר הורוביץ.
 +
:[[משתמש:Gordo6|גל א.]]
 +
::לא בדיוק - גם בקבוצה של שיין לופיטל בחומר.
  
−
===תשובה===
+
== שאלה על פתרון שאלה ==
−
חובה גם להוכיח שזה מתכנס. אבל אני לא רואה איך אפשר למצוא את הסכום בלי להוכיח שזה מתכנס ממילא... --[[משתמש:ארז שיינר|ארז שיינר]] 02:44, 25 בנובמבר 2010 (IST)
+
  
−
== תרגיל 7 ==
+
תרגיל 10 (http://www.math-wiki.com/images/d/db/10Infi1Targil10Sol.pdf) שאלה 2- כתבתם שקיים M כך ש fx<M>-אמ. אבל אז בפונקציה g לקחתם את הערך 1/M+1 - והרי איך אפשר לדעת בוודאות שהפונקציה רציפה בו (צריך שהיא תהיה רציפה כדי להשתמש במשפט ערך הביניים)? אם f חסומה בין שליש למינוס שליש, אז 1/M+1 הוא 4, והפונקציה מ2 ל4 לא בהכרח רציפה!
 +
:אפשר לקחת M גדול כרצוננו, הרי זה חסם. אם היא חסומה על ידי שליש, היא בוודאי גם חסומה על ידי אחד --[[משתמש:ארז שיינר|ארז שיינר]] 13:58, 29 בינואר 2011 (IST)
 +
::אוקי.
  
−
כאשר אני בודקת התכנסות בהחלט האם אפשר להשתמש בכל המבחני השוואה לטורים חיוביים?
+
== עזרה בשאלה ממבחן ==
  
−
===תשובה===
+
תהי {an} כך שלכל K טבעי <math>a_{2k+1}-a_{2k-1}<0 \and a_{2k+2}-a_{2k}>0</math>, וגם ש <math>lim_{n->infinity}a_{n+1}-a_n=0</math>. הוכח שהסדרה מתכנסת. תודה!
−
אם מדובר בטור חיובי, מותר להשתמש במבחני ההשואה לטורים חיוביים, אם לא אז לא. נא לחדד את השאלה. --[[משתמש:ארז שיינר|ארז שיינר]] 18:31, 23 בנובמבר 2010 (IST)
+
  
−
== התכנסות טורים ==
+
:יש תת סדרה מונוטונית עולה, ותת סדרה מונוטונית יורדת. אתה צריך להראות ששתיהן חסומות ולכן מתכנסות, ואחר כך שבהכרח לאותו הגבול. --[[משתמש:ארז שיינר|ארז שיינר]] 13:55, 29 בינואר 2011 (IST)
 +
::הבנתי אותך. רק לא הצלחתי להוכיח שהתת סדרות חסומות. אפשר עזרה?
 +
:::הסדרה העולה חייבת להיות קטנה מהסדרה היורדת. אם הן היו עוברות אחת את השנייה, ההפרש בין שני איברים עוקבים לא היה יכול לשאוף לאפס. --[[משתמש:ארז שיינר|ארז שיינר]] 17:06, 29 בינואר 2011 (IST)
 +
::::אוקי..
  
−
בניגוד לבסדרות, שבהן למדנו שסכום ומכפלת סדרות מתנכסות מתכנסים, בטורים למדנו רק על סכום.(עריכה) זה אומר שמכפלת טורים  מתכנסים לא בהכרח מתכנסת? תודה!
+
== עזרה בשאלה נוספת ממבחן ==
  
−
===תשובה===
+
יהי n טבעי, נניח f מוגדרת וגזירה n פעמים בסביבת 0, ו f0=f'0=f''0=..=f^(n-1)(0)=0 (נגזרות ב0)., f^(n)(0)=5. חשב <math>lim_{x->0}(fx/(sin2x)^n)</math>. תודה מראש
−
אני מניח שאתה שואל לגבי מכפלת טורים. מכפלת סדרות הוא כפל איבר איבר, כלומר <math>c_n=a_n\cdot b_n</math>. אם תגדיר באופן דומה מכפלת טורים, ה"מכפלה" לא בהכרח תתכנס, ואם כן, בוודאי לא למכפלת הסכומים. דוגמאות:
+
:אני מניח שלקחת את השאלה הזו מתוך מבחן של ד"ר הורוביץ (עשיתי אותה לפני כעשר דקות). שים לב לרמז שמופיעה מתחתיה (כאשר x->0 יתקיים ש sinx/x->1), היעזר בו למציאת פונקציה שתהיה במכנה שתהיה נוחה לגזירה, והשתמש בכלל לופיטל n פעמים. מקווה שעזרתי, [[משתמש:Gordo6|גל א.]]
 +
::לא הבנתי איך אפשר להשתמש ברמז כדי לפתור את התרגיל- גזרתי את הפונקציה עם לופיטל N פעמים ואף פעם לא היה "x" - רק סינוס, קוסינוס ודברים שקשורים לn. לא הבנתי מה זה אומר למה התכוונת כשאמרת להיעזר בו כדי למצוא פונקציה במכנה נוחה לגזירה.
 +
:::<math>Lim\frac{f(x)}{(sin2x)^n}=Lim\frac{f(x)}{(2x)^n}*\frac{(2x)^n}{(sin2x)^n}=...=Lim\frac{f(x)}{(2x)^n}</math> כל הגבולות כאשר איקס שואף לאפס. כעת הפונקציה במכנה "נוחה לגזירה". מה הנגזרת ה-nית שלה? הפעל את כלל לופיטל עבור הנגזרת ה-nית, קבל מסקנה עבור הנגזרת ה-(n-1) והפעל את הכלל שוב ושוב עד שתקבל מסקנה על הפונקציה המקורית. מקווה שעזרתי, [[משתמש:Gordo6|גל א.]]
 +
::::נראה לי שהבנתי. האם הפתרון הוא 5 חלקי N עצרת כפול 2 בחזקת N?
 +
:::::אכן.
  
 +
== רציפות במ"ש ==
  
−
* <math>1=\sum a_n=\sum\frac{1}{2^n}</math>, אבל <math>\sum a_n^2 = \sum \frac{1}{2^{2n}} <1 \neq 1\cdot 1</math>
+
מישהו יכול לעזור לי למצוא שתי סדרות כדי להפריך רציפות במ"ש של פונקציות xsinx xcosx?
−
* <math>\sum a_n=\sum\frac{(-1)^n}{\sqrt{n}}</math> מתכנס לפי לייבניץ, אבל אם תכפול אותו בעצמו תקבל את הטור ההרמוני שאינו מתכנס.
+
:<math>f(x)=xsinx</math> ו<math>x_n=2\pi k, y_n=2\pi k + \frac{1}{k}</math>. אזי <math>f(y_n)-f(x_n)=2\pi k sin(\frac{1}{k}) + \frac{1}{k}sin(\frac{1}{k}) \rightarrow 2\pi + 0 \neq 0</math> --[[משתמש:ארז שיינר|ארז שיינר]] 17:11, 29 בינואר 2011 (IST)
  
−
הדרך הנכונה לכפול טורים, בדומה למכפלת סכום, צריכה להוסיף מחוברים רבים אחרים. <math>(a_1+a_2)(b_1+b_2)=a_1b_1+a_2b_2+{\color{red}a_1b_2+a_2b_1}</math>. יש משפטים בנוגע למכפלת טורים, אני לא יודע אם אתם לומדים אותם. --[[משתמש:ארז שיינר|ארז שיינר]] 01:27, 25 בנובמבר 2010 (IST)
+
== קירוב ליניארי ==
−
:לא למדנו עוד את לייבניץ אבל הבנתי את התשובה, תודה רבה!
+
  
−
== משהו לא מובן לגבי טורים... ==
+
היי ארז,
  
−
בקשר לטורים וסדרת הסכומים החלקיים שלהם-
+
באחד המבחנים ביקשו להגדיר את הקירוב הליניארי ולהסביר את חשיבותו....
−
אם הסדרה של הס"חים מתכנסת אז הטור בהכרח מתכנס? או שהסדרה של הס"חים חייבת להתכנס לאפס? כי יש  משפט שאומר שאם הטור מתכנס, אז הסדרה של הס"חים מתכנסת לאפס, אני צודק? אז זה אומר שאם יודעים שסדרה של ס"חים מתכנסת אז היא בוודאי מתכנסת? ואם אני יודע שסדרה של ס"חים מתכנסת אבל לא לאפס, זה אומר שהטור מתבדר? תודה
+
  
−
===תשובה===
+
איך מגדירים זאת בצורה מדוייקת ומה ההסבר הנדרש פה?
−
תבדיל בין סדרת הסכומים החלקיים, לסדרה של הטור. כלומר, <math>\sum a_n</math> הינו טור, הוא סכום איברי הסדרה <math>a_n</math>. סדרת הסכומים החלקיים הינה <math>S_n=\sum_{i=1}^na_i</math>.
+
  
−
'''לפי הגדרה''' טור מתכנס אם סדרת הסכומים החלקיים שלו <math>S_n</math> מתכנסת, וסכום הטור מוגדר להיות גבול סדרת הסכומים החלקיים. אין הגדרה אחרת להתכנסות טור. סדרת הסכומים החלקיים יכולה להתכנס לכל גבול, ואין לה קשר מיוחד לאפס.
+
תודה!
  
−
לפי משפט, אם טור מתכנס, הסדרה שלו שואפת לאפס, כלומר <math>\lim a_n = 0</math>. אבל, אם הסדרה הזו שואפת לאפס, אין זה אומר בהכרח שהטור מתכנס (לדוגמא - הטור ההרמוני <math>\sum{1}{n}</math>). --[[משתמש:ארז שיינר|ארז שיינר]] 01:31, 25 בנובמבר 2010 (IST)
+
:אני לא בטוח למה הוא מכוון בשאלה, עניתי על זה בתרגיל החזרה. מגדירים את זה בצורה מדוייקת (יש את הנוסחא בדפי התרגיל) ולדעתי ההסבר הוא שניתן כך להעריך פונקציות מבלי להיות מסוגלים לחשב אותן במפורש כאשר אנו כן יודעים לחשב את הפונקציה ואת הנגזרת קרוב לערך המבוקש. --[[משתמש:ארז שיינר|ארז שיינר]] 16:56, 29 בינואר 2011 (IST)
−
:בדיוק מה שהייתי צריך, תודה רבה.
+
  
−
== האם הטענה נכונה? (על התכנסות סדרות) ==
+
== עזרה בפתרון שאלה ==
  
−
האם זה נכון להגיד, שאם מכפלה של סדרה לא חסומה(ולא מתכנסת) כפול סדרה מתכנסת, היא מתכנסת, אז הסדרה השנייה מתכנסת לאפס? כלומר: an סדרה לא חסומה, bn סדרה מתכנסת, cn=anbn, אז זה נכון שאם cn מתכנסת אז bn מתכנסת לאפס? (נראה לי שזה נכון אבל אני רוצה להיות בטוח כי הרבה פעמים יש לי טעויות.) תודה!
+
שאלתי את השאלה קודם, אך אני לא בטוח שהפתרון שנתנו לי נכון, לכן אבקש, ארז, אם תוכל, לבדוק שהפתרון שנתנו אכן נכון. הנה השאלה [[http://math-wiki.com/index.php?title=%D7%A9%D7%99%D7%97%D7%94:88-132_%D7%A1%D7%9E%D7%A1%D7%98%D7%A8_%D7%90'_%D7%AA%D7%A9%D7%A2%D7%90#.D7.A2.D7.96.D7.A8.D7.94_.D7.91.D7.A4.D7.AA.D7.A8.D7.95.D7.9F_.D7.A9.D7.90.D7.9C.D7.94]]. תודה!
  
−
===תשובה===
+
:לא קראתי את הפתרון הזה, אבל פתרתי את זה בכיתה בשיעור החזרה. אם a_n אינה קושי, אז היא אינה מתכנסת ולכן הגבול החלקי העליון והתחתון שלה שונים, לכן יש לה תת סדרה ששואפת לעליון ותת סדרה ששואפת לתחתון. ניתן לכן לבנות תת סדרה אחרת כך שאיברים הזוגיים שלה יהיו מהראשונה והאיבריים האי זוגיים שלה יהיו מהשנייה. עבור תת סדרה זו, <math>\lim |a_{n_{k+1}}-a_{n_k}| = \limsup - \liminf \neq 0</math> בסתירה. --[[משתמש:ארז שיינר|ארז שיינר]] 16:52, 29 בינואר 2011 (IST)
−
זה נכון. לסדרה שאינה חסומה יש תת סדרה ששואפת לאינסוף. לכן אם b_n שואף למספר ששונה מאפס לc_n תהיה תת סדרה ששואפת לאינסוף (כי מספר קבוע כפול אינסוף נשאר פלוס מינוס אינסוף, חוץ מאשר אפס). --[[משתמש:ארז שיינר|ארז שיינר]] 19:16, 25 בנובמבר 2010 (IST)
+
::תודה.
−
:תודה
+
  
−
== מציאת סכומים של טורים... ==
+
== מישפט היינה בורל  ==
  
−
בקשר למציאת הסכום עצמו של טור מתכנס, אני זוכר שלמדנו רק על איך מוצאים סכום של סדרה הנדסית מתכנסת, ואולי מקרים מיוחדים כמו סכום טלסקופי וכו'. האם ישנם עוד דרכים? אולי יש קשר בין הגבול שאליו מתכנסת סדרת הטור לבין סכום הטור? או שיש דרך אחרת למצוא סכום של טור? תודה!
+
מישהוא יכול ליכתוב אותו בבקשה
 +
:"יהי <math>K</math> קטע סגור, ויהיו <math>\{I_a\}_{a\ in\ A}</math> קטעים פתוחים ב-<math>\R</math> כך ש-<math>K</math> מוכל ממש באיחוד של כולם. אזי קיים מספר סופי של קטעים כאלו כך ש-<math>K</math> מוכל ממש בתוך האיחוד שלהם". (אני לא הייתי בהרצאה הזו, זה מתוך מחברת שצילמתי ממישהו). מקווה שעזרתי [[משתמש:Gordo6|גל א.]]
  
−
:סדרה הנדסית וטור טלסקופי זה נכון. בכלל, כל דבר שאתה יודע לחשב היטב את סדרת הסכומים החלקיים שלו. אם מדובר בתרגיל 6, שים לב שאתה יכול להפריד לשברים. --[[משתמש:ארז שיינר|ארז שיינר]] 19:04, 25 בנובמבר 2010 (IST)
+
תודה פשוט בוויקפדיה זה רשום  בצורה קצת פחות פורמלית
  
−
==שאלה 1 א תרגיל 7==
+
אולי יש לכה במיקרה גם את המישפט של בולצאנו ויירשטראס לקבוצות
−
אני יודע שהטור an אינו מתכנס בהחלט:
+
:"תהי <math>S</math> קבוצה המוכלת ממש בממשיים, קבוצה אינסופית אך גם חסומה. אזי קיימת לה נקודת הצטברות". מקווה שעזרתי, [[משתמש:Gordo6|גל א.]]
−
כלומר: או שהטור an מתבדר או שהוא מתכנס על תנאי
+
::אגב, אני לומד אצל ד"ר הורוביץ. אם אתה לא לומד אצלו, ייתכן שהמרצה שלך ניסח את זה קצת אחרת, אבל בסופו של דבר זה אותם משפטים.
−
בנסוף אני יודע שan היא סדרה מתכנסת ל 0 אך היא לא מונוטונית יורדת,כלומר מכאן שהטור לא מקיים ת משפט לייבניץ,
+
:::בולצאנו-ויירשטראס זה לא זה שלכל סדרה חסומה יש תת סדרה מתכנסת?
−
איך אני מחליט כעת אם הוא מתבדר או מתכנס על תנאי?
+
::::אני מנחש שהוא מתכוון לגרסא: "לכל קבוצה אינסופית וחסומה יש נקודות הצטברות" --[[משתמש:ארז שיינר|ארז שיינר]] 19:26, 30 בינואר 2011 (IST)
  
−
===תשובה===
+
== עזרה בבדיקת היתכנסות הטור ==
−
קודם כל הסדרה כן מונוטונית יורדת לאפס, הרי בודקים את בלי הסימן. אבל אין שם פלוס מינוס לסירוגין כמו לייבניץ, אלא מינוס פעם ב3 איברים. אפשר לחלק את הטור לשניים ולהגיע לתוצאה מעניינת. --[[משתמש:ארז שיינר|ארז שיינר]] 11:13, 26 בנובמבר 2010 (IST)
+
  
 +
<math>\sum \frac{(2n)!}{(2n)^{2n}}</math>
 +
:{{לא מתרגל}} מתכנס, אני מיד אכתוב למה.
 +
:{{הערה|חזרתי:}}
 +
{|
 +
{{=|l=\overline{\lim_{n\to\infty} }\frac{(2n+2)!/(2n+2)^{2n+2} }{(2n)!/(2n)^{2n} }
 +
  |r=\overline{\lim}\frac{(2n)!(2n+1)(2n+2)(2n)^{2n} }{(2n)!(2n+2)^{2n}(2n+2)^2 }
 +
}}
 +
{{=|r=\lim\left(\frac{2n+1}{2n+2}\cdot\left(\frac{2n}{2n+2}\right)^{2n}\right)
 +
}}
 +
{{=|r=\lim\frac{2n+1}{2n+2}\ \cdot\ \lim\left(\left(1+\frac1n\right)^n\right)^{-2}
 +
}}
 +
{{=|r=1\cdot e^{-2}
 +
}}
 +
{{=|r=1
 +
  |o=<
 +
}}
 +
|}
 +
:והודות לד'אלמבר הטור (שהוא טור חיובי) מתכנס. {{משל}}
 +
פשש  זה בדיוק מה שלא ראיתי החלק של המנה שמיתכנס ל e תודה רבה
  
 +
== בקשה ==
  
−
==המשך==
+
שלום רב,
 +
למישהו יש מושג איך לפתור את שאלה 1א במבחן הזה: http://www.studenteen.org/inf1_exam_blei_2008_a.pdf
 +
תודה מראש!
 +
:{{לא מתרגל}} יש לי רעיון מתחכם, אבל יקח לי קצת זמן לכתוב אותו.
 +
::יש סיכוי שתכתוב אותו כאן בכל זאת היום או מחר? תודה מראש!
 +
:::{{לא מתרגל}}הרעיון הכללי - נוכיח שזה שואף לאינסוף. לשם כך מוכיחים שהטור <math>\sum \frac{2^n n! (4n)^n}{(4n)!}</math> מתכנס (מבחן ד'אלמבר), לכן <math>\frac{2^n (n!) (4n)^n}{(4n)!}\to0</math> ולכן (מכיוון שהסדרה הזו חיובית), <math>\frac{(4n)!}{2^n (n!) (4n)^n}\to\infty</math>. אח"כ, מכיוון ש-<math>\forall n\in\mathbb N:\ \binom{3n}{n}\ge1</math>, מתקיים <math>\forall n\in\mathbb N:\ \sqrt[n]{\binom{3n}{n}}\ge1</math> ולבסוף נקבל שהסדרה הכללית מתכנסת במובן הרחב לאינסוף. {{משל}}
 +
::::או, זה יפה ^^
  
−
הצלחתי להוכיח שהחיוביים דואפים ל + אינסוף ושהשליליים ל - אינסוף אבל עדיין,איך מכאן אני יכול לדעת אם הסדרה מתכסת התנאי או מתבדר
+
== שאלה אלמנטרית ==
  
−
:בשום דרך. תנסה לעשות חלוקה אחרת שכן תעזור לפתור את התרגיל (הרי אי אפשר לדעת מה זה אינסוף ועוד מינוס אינסוף, אבל כן אפשר לדעת אינסוף ועוד אינסוף) --[[משתמש:ארז שיינר|ארז שיינר]] 13:02, 26 בנובמבר 2010 (IST)
+
המרצה שלנו כתב בתחילת הקורס: P בריבוע זוגי -> P זוגי. זה כנראה נכון רק כאשר P שלם. יש לזה הוכחה קלה?
  
−
== התכנסות זנבות ==
+
:גם אני חיפשתי הוכחה עוד מזמן, והגעתי למסקנה שההוכחה היא פשוט של-p בריבוע יש את כל הגורמים של p, פעמיים. אז אם הוא זוגי זה אומר שיש לו את הגורם 2. נניח בשלילה של-p אין את הגורם 2. אבל ל-p בריבוע יש את הגורם 2, לכן חייב להיות ל-p את שורש 2. בסתירה לכך שהוא שלם. לכן יש ל-p את הגורם 2 כלומר הוא זוגי.
  
−
האם זה נכון להגיד שיש קשר אמ"מ בין התכנסות סדרה לבין התכנסות הזנבות שלה?
+
::זה נכון עבור שלמים, אחרת אין משמעות לזוגי. זה נובע מחומר שהוא לא של הקורס הזה. יש משפט שאומר שאם ראשוני מחלק את ab אז הוא מחלק את a או מחלק את b, לכן אם 2 מחלק את aa=a^2 סימן שהוא מחלק את a. --[[משתמש:ארז שיינר|ארז שיינר]] 13:08, 30 בינואר 2011 (IST)
  
−
:<s>זה מה שנובע מהתרגיל, בסופו של דבר. --[[משתמש:ארז שיינר|ארז שיינר]] 13:03, 26 בנובמבר 2010 (IST)</s>
+
:::ואני הופתעתי שלא מצאתי דרך מתמטית להוכחה אפילו שהמרצה כתב "קל להוכיח ש...".
−
:לא קראתי את השאלה טוב. התכנסות סדרה? בוודאי שלא. הרי לא לכל סדרה מתכנסת הטור מתכנס. --[[משתמש:ארז שיינר|ארז שיינר]] 13:47, 26 בנובמבר 2010 (IST)
+
  
−
==שאלה==
+
== חתכי דדקינד ==
  
−
האם מותר לי להשתמש במשפט דיריכלה שאותו לא למדנו במסגרת אינפי 1 כדי להוכיח את שאלה 3
+
לקבוצה של ד"ר שיין תהיה במבחן שאלה על חתכי דדקינד. הבעיה היא שלא היה תרגול בנושא, וגם אין שאלות עם תשובות במיזלר או בכל מקום אחר שבו חיפשתי.
−
:אסור להשתמש במשפטים שלא הפיעו בהרצאה או בתרגול. --[[משתמש:ארז שיינר|ארז שיינר]] 13:48, 26 בנובמבר 2010 (IST)
+
  
−
== התכנסות סדרה הנדסית ==
+
שיין מסר 3 תרגילים בנושא, אבל אין לי מושג לאיזה פתרון הוא מצפה. כלומר, מה הכוונה "שפה של חתכי דדקינד"? אפשר בבקשה לראות פתרון של אחת או כמה מהשאלות הבאות: http://sites.google.com/site/eduardkontorovich/home/%D7%94%D7%9B%D7%A0%D7%94%D7%9C%D7%9E%D7%91%D7%97%D7%9F.pdf?attredirects=0&d=1 בבקשה ותודה רבה מראש!
 +
:מצטרף, במיוחד אם אפשר את הפתרון לשאלה 1 (הפתרון היחיד שאני מצאתי הוא "שסדרת החסמים העליונים של An מתכנסת", אבל סדרת החסמים העליונים של An היא בעצם סדרת הממשיים הנוצרים ע"י החתכים, כלומר לא אמרתי כלום בפתרון הזה.)
  
−
רוצים לדעת מתי טור סדרה הנדסית מתכנס, ולאיזה סכום. כלומר יהי q כלשהו, רוצים לדעת מהו <math>\sum_{n=1}^\infty a_n =\sum_{n=1}^\infty q^n</math>.
+
::לי בפתרון חשוב במיוחד לראות את הנימוקים והניסוח, כלומר ה"שפה" של דדקינד. אז למרות שאני חושבת שאני יודעת את התשובה הסופית של 1, יעזור לי מאוד מאוד לראות פתרון מלא של 100 במבחן. אז התשובה, כלומר התנאי, הוא: לכל אפסילון חיובי קיים N כך שלכל n טבעי גדול מ-N, מתקיים שהקבוצה <math>A_n/A_{L-\epsilon}</math> מוכלת ב-<math>(L-\epsilon,L)</math>. בעצם שינוי של ההגדרה של ההתכנסות.
 +
:::התבלבלת, מה זה An/A_L-e?
 +
::::לא התבלבלתי, זה הקבוצה <math>A_n</math> בלי הקבוצה <math>A_{L-\epsilon}</math>. תיזכר בסימונים של בדידה.
 +
:::::אוקי.. אבל אני לא רואה איך התנאי פה קשור להתכנסות של סדרת המספרים. אולי תסבירי מה הכוונה פה. אבל בעצם, הרעיון הזה של לקחת את תנאי ההתכנסות למספרים ולהעתיק אותו לחתכים הוא רעיון ממש טוב, נראה לי שהוא יכול לעבוד. בזכות הרעיון שלך פתרתי את זה כך: צריך לעשות קודם כמה הכנות. נגדיר: חתך  A הוא "חיובי" אם המס' שמייצר אותו (תמיד קיים) גדול מאפס, או במילים אחרות שכל מספר שקטן nאפס שייך לA (כנ"ל עם שלילי, אי שלילי וכו'). (הערה- כשאני אומר חתך A אני מתכוון לחתך A,A'). כמו כן "A-" הוא החתך שמייצר את המספר הנגדי לA, והרי הוכחנו בכיתה שלכל מספר ממשי יש נגדי ושכל מספר מיוצר ע"י חתך יחיד (כי אם המספר רציונלי, ניקח תמיד חתך מהסוג הראשון, ואם המספר אי רציונלי ניקח חתך מהסוג השלישי), ולכן ההגדרה טובה, ולבסוף נגדיר "|A|" כ-A אם A חיובי וכ- A- אם A שלילי, וב0 ברור. כעת התנאי יהיה שאם לכל אפסילון גדולה E (חתך) חיובית (גדולה מאפס=חיובית כמו שהגדרתי) קיים N כך שלכל n>N מתקיים שהחתך |An-L| מוכל בחתך E. (שוב, החלק השמאלי של החתך), אז סדרת החתכים מתכנסת לL. עכשיו רק צריך להוכיח שזה תנאי הכרחי ומספיק. אולי אנסה בהמשך ואגיד לך אם יש תוצאות..
  
−
למדנו כבר ש<math> |q|<1\iff\lim_{n\rightarrow\infty}q^n=0</math>, לכן עבור <math>|q|\geq 1</math> הטור בהכרח מתבדר.
 
  
−
עבור <math>|q|<1</math>, נסתכל על סדרת הסכומים החלקיים. <math>S_n=a_1+...+a_n=q+q^2+...+q^n=q\frac{1-q^n}{1-q}</math>. אבל סכום הטור '''מוגדר''' להיות גבול סדרת הסכומים החלקיים, וגבול הסדרה הזו הינו <math>\frac{q}{1-q}</math> מכיוון שכפי שהזכרנו למעלה, <math>q^n \rightarrow 0</math>.
+
http://dl.dropbox.com/u/2237179/infi1dedekind.pdf
 +
:לא הבנתי אף אחד מהפתרונות שלו ואני גם לא בטוח שהם נכונים.
 +
'''מי כתב את הפתרון הזה?'''
 +
::זה מה ששיין שלח לתלמידים שלו במייל. תודה שיין, אבל זה כל כך לא בסדר ומלחיץ שלא פתרנו תרגילים כאלו קודם...
  
−
--[[משתמש:ארז שיינר|ארז שיינר]] 15:48, 26 בנובמבר 2010 (IST)
+
== בפתרון למבחן של זלצמן 2010 ==
  
−
== שאלונת על ln n ==
+
כתוב בפיתרון לשאלה 5.ג
 +
ש<<math>e^{(x^2)}</math> רציפה במ"ש.
  
−
הסדרה an=ln n מתכנסת לאינסוף? תודה!
+
למה זה נכון?
  
−
===תשובה===
+
:זה לא נכון, וגם לא רשום שם. רשום שם שהיא רציפה, ובגלל שסינוס גם רציפה, ההרכבה רציפה ומחזורית ולכן '''ההרכבה''' רציפה במ"ש. --[[משתמש:ארז שיינר|ארז שיינר]] 13:12, 30 בינואר 2011 (IST)
−
כן. יותר מזה, lnx הינה פונקציה מונוטונית כלומר אם a>b אזי גם lna > lnb. זה נכון מכיוון שe^x הינה פונקציה מונוטונית, וln היא ההופכית שלה. --[[משתמש:ארז שיינר|ארז שיינר]] 17:14, 26 בנובמבר 2010 (IST)
+
  
−
== שאלה על סדרות וטורים ==
+
== כלל לופיטל ==
  
−
עם הסדרה של הטור (לא סדרת הסכומים החלקיים) מתבדרת, אפשר להגיד שהטור מתבדר או שזה לא נכון? תודה!
+
כלל לופיטל הוא בחומר של הקבוצה של שיין?
 +
:למדנו את זה אז כנראה שכן...
 +
 
 +
== כלל לופיטל ==
 +
 
 +
האם אפשר להשתמש בכלל לופיטל כדי למצוא גבולות בקצוות כאשר בודקים רציפות במ"ש של פונקציה?
 +
 
 +
:לדעתי כן, מומלץ לשאול את המרצה או המתרגל בעת המבחן בנוסף. --[[משתמש:ארז שיינר|ארז שיינר]] 13:24, 30 בינואר 2011 (IST)
 +
 
 +
== מבחני קושי ודלמבר ==
 +
 
 +
מבחן קושי הוא עם limsup בשני המקרים (התכנסות והתבדרות) ומבחן דלמבר הוא עם limsup במקרה של התכנסות ו liminf במקרה של התבדרות, או שיש לי טעות? תודה!
 +
:אין טעות. תסתכל על ההוכחות שלהם ותבין למה.
 +
 
 +
== חקירת פונקציות, המבחן של ד"ר הורוביץ ==
 +
 
 +
צריך לזכור בעל-פה את הסדר של הסעיפים בחקירת פונקציות? (תחום הגדרה ונקודות אי רציפות, האם הפונקציה זוגית/אי-זוגית/לא זה ולא זה, אסימפטוטות, תחומי עלייה+ירידה+נקודות קריטיות, תחומי קעירות+קמירות+נקודות פיתול, טבלת ערכים)<br/>או שזה כתוב במבחן?
 +
:הוא אמר שלא בטוח שהוא יכתוב את זה. אבל הוא גם אמר שאין חובה לעשות לפיהסדר שהוא רשם אם כל הסעיפים כלולים. [[משתמש:Gordo6|גל א.]]
 +
 
 +
== [[מדיה:10Infi1TargilFinalGrades.pdf|ציונים]] ==
 +
 
 +
מספר תעודת הזהות שלי (312491822), ואפילו לא מספר דומה לו, לא מופיע בדף הציונים שפורסם היום. אתם יכולים לבדוק את זה? תודה רבה
 +
:יתכן ואתה תיכוניסט? אלו ציונים רק לתלמידים של זלצמן.
 +
::כן, תיכוניסט. תודה
 +
:::הציונים של התיכוניסטים שאדוארד מתרגל מופיעים באתר שלו: sites.google.com/site/eduardkontorovich
 +
 
 +
== איקס בריבוע ==
 +
 
 +
איך מוכיחים ש-<math>x^2</math> לא רציפה במ"ש? תודה.
 +
:{{לא מתרגל}}ראה [[מדיה:10Infi1Targil8Sol.pdf|פתרון תרגיל 8]], שאלה 9.
 +
::תודה.
 +
 
 +
== שאלה קלה מדי? ==
 +
 
 +
צ"ל או להפריך שאם הטור an מתכנס והטור bn מתבדר אז הטור an+bn מתבדר. לכאורה אפשר להניח בשלילה שהטור an+bn מתכנס, ואז הטור an + הטור bn מתכנס (*), לכן הטור an ועוד הטור bn פחות הטור an = הטור bn מתכנס, בסתירה. אבל ב-(*) הזזנו את המקום של אינסוף איברים, ולכן ההוכחה לא מספיקה. מה לעשות? (ניסיתי לרפד באפסים כמו שכתוב ב[[שיחה:88-132 סמסטר א' תשעא/ ארכיון 15#משפט רימן|ארכיון 15]])
 +
:מישהו יודע?
 +
 
 +
== פתרון של הבחינות ==
 +
 
 +
הי ארז,
 +
 
 +
ראשית תודה שהעלת לנו את הפתרון לבחינות כל כך מהר. יתכן ששאלתי לא במקום משום שאני לא לומד אצל זלצמן - אבל מה עם הפתרון לשאלות 3 ו-6 בבחינה שלו? הן היו שאלות של ציטוט משפטים?
 +
 
 +
אגב, אולי לבחינות של התיכוניסטים כדאי להוסיף הבהרה ששאר השאלות שלא פורסם להן פתרון היו בבחינה של זלצמן (שאלה 1 של הורוביץ = שאלה 1 של זלצמן, שאלה 2 של הורוביץ = שאלה 7 של זלצמן, שאלה 4 של הורוביץ = שאלה 4 של זלצמן, שאלה 5 של הורוביץ = שאלה 2 של זלצמן). כמו כן כדאי להוסיף שהבחינה של ד"ר שיין זהה לבחינה של ד"ר הורוביץ, למעט בשאלה 6 שעסקה בחתכי דדקינד.
 +
 
 +
כעת שאלה לגבי הפתרונות עצמם: בשאלה 5ג (של זלצמן) כתבת ששורש איקס רציפה בכל הממשיים, אבל זה כמובן לא נכון כי היא מוגדרת רק בממשיים החיוביים. האם יש דרך אחרת להוכיח רציפות במ"ש בסעיף זה בלי להתבסס על טענה זו?  
 +
 
 +
שוב תודה על פרסום הפתרונות (במיוחד עבור המבחן של ד"ר הורוביץ שזה בכלל לא מובן מאליו).
  
 
===תשובה===
 
===תשובה===
−
כן, כי יש משפט שאומר שהסדרה של טור מתכנס תמיד שואפת לאפס. אם היא מתבדרת, בפרט, היא אינה שואפת לאפס ולכן זו תהיה סתירה אם הטור יתכנס. --[[משתמש:ארז שיינר|ארז שיינר]] 17:15, 26 בנובמבר 2010 (IST)
+
שאלה 3 הייתה ציטוט משפטים, שאלה 6 עסקה בנגזרות, ושאלה 8 הייתה להוכיח את משפט קנטור - לא כתבתי להן פתרונות, כמו כן לא כתבתי פתרון לשאלה על חתכי דדיקינד.
−
:לא - התכוונתי ההפך, כלומר המשפט הוא לא אם ורק אם. הרי טור יכול להתבדר גם אם הסדרה שלו לא שואפת לאפס. אבל יש מקרה אחד שנראה לי שכן אפשר לדעת שהטור מתבדר לפי הסדרה שלו-- אם הסדרה שלו מתבדרת, (בעצם, אם הסדרה שואפת לאינסוף, כי למשל הטור של מינוס אחד בחזקת n מתכנס לאפס) אז הטור מתבדר. זה נכון?
+
 
−
::המשפט אומר שאם טור מתכנס אז הסדרה שלו מתכנסת לאפס. התנאי הזה שקול לוגית לתנאי אם הסדרה של טור מסוים לא מתכנסת לאפס אז הטור מתבדר (בדוק את זה! באופן כללי, הטענה <math>a =>b</math> שקולה לטענה <math>not b => not a</math>, כפי שהוסבר לנו בקורס מתמטיקה בדידה (בסמסטר הקיץ האחרון)). לכן אם הסדרה של הטור תתבדר אז וודאי שהיא לא שואפת לאפס ולכן הטור יתבדר. מקווה שעזרתי, [[משתמש:Gordo6|גל א.]]
+
לגבי 5ג, לא צריך ששורש איקס יהיה רציף במ"ש על כל הממשיים, אלא רציף במ"ש בתמונה של הפונקציה עליה הוא מורכב - במקרה זה הערך המוחלט ותמונתו <math>[0,\infty)</math> ולכן זה פתרון תקין.
 +
 
 +
====תשובה====
 +
אוקי, שוב תודה :-)

גרסה אחרונה מ־15:34, 5 בפברואר 2011

חזרה לדף הקורס


גלול לתחתית העמוד


הוספת שאלה חדשה

הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).

-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן

אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.

ארכיון


שאלות

הערה בקשר למבחן ביום שני

אני תלמיד של מיכאל שיין ולא היה לנו תרגול אחד על חתכי דדקינד בכל הסמסטר ואני בספק אם מישהו יודע איך לפתור את התרגילים בנושא חתכי דדקינד.

אשמח אם תתחשבו בנו.

מצטרפת. לא היו שיעורי בית בנושא, בהרצאה לא פתרנו תרגילים, ואין במיזלר. אשמח אם תענו לי למטה על השאלה לגבי חתכי דדקינד.


מצטרף גם.. אין לנו מושג איך לגשת לתרגילים האלו כי אף פעם לא הראנו לנו איך לפתור תרגילים כאלה.. אפשר להעלות חומר ללימוד או לפחות פתרון לתרגיל שאדווארד העלה לאתר: http://sites.google.com/site/eduardkontorovich/

אני חושב שכמעט אף אחד בקבוצה לא יודע לפתור תרגילים כאלה..

ואם מישהו יודע (ולא נראה לי), אז הוא בטוח למד ממקור נוסף שאני לא מכירה.

http://dl.dropbox.com/u/2237179/infi1dedekind.pdf

שאלה בקשר למבחן ביום שני

מישהו יכול בבקשה לפרט אילו שאלות עלולות להופיע במבחן באינפי 1 ביום שני? יופיעו שאלות חישוביות? תודה.

תלוי באיזו קבוצה אתה. אם אתה אצל התיכוניסטים, מבנה המבחן הוא כדלקמן:
יש שש שאלות ואין בחירה ביניהן, סה"כ זמן המבחן שעתיים וחצי. כל שאלה 18 נקודות = סה"כ 108 נקודות.
תהיה שאלה על סדרות, על טורים, על פונקציות (גבולות וכדומה), רציפות/רציפות במ"ש, נגזרות ויישמון של נזגרות (טיילור, לופיטל וכו...). עבור תלמידיו של ד"ר שיין - יהיו חתכי דדקינד במקום ישומי הנגזרות.
כל מה שנכתב כאן נאמר על ידי ד"ר הורוביץ.
גל א.
לא בדיוק - גם בקבוצה של שיין לופיטל בחומר.

שאלה על פתרון שאלה

תרגיל 10 (http://www.math-wiki.com/images/d/db/10Infi1Targil10Sol.pdf) שאלה 2- כתבתם שקיים M כך ש fx<M>-אמ. אבל אז בפונקציה g לקחתם את הערך 1/M+1 - והרי איך אפשר לדעת בוודאות שהפונקציה רציפה בו (צריך שהיא תהיה רציפה כדי להשתמש במשפט ערך הביניים)? אם f חסומה בין שליש למינוס שליש, אז 1/M+1 הוא 4, והפונקציה מ2 ל4 לא בהכרח רציפה!

אפשר לקחת M גדול כרצוננו, הרי זה חסם. אם היא חסומה על ידי שליש, היא בוודאי גם חסומה על ידי אחד --ארז שיינר 13:58, 29 בינואר 2011 (IST)
אוקי.

עזרה בשאלה ממבחן

תהי {an} כך שלכל K טבעי 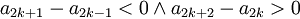a_{2k+1}-a_{2k-1}<0 \and a_{2k+2}-a_{2k}>0, וגם ש 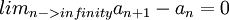lim_{n->infinity}a_{n+1}-a_n=0. הוכח שהסדרה מתכנסת. תודה!

יש תת סדרה מונוטונית עולה, ותת סדרה מונוטונית יורדת. אתה צריך להראות ששתיהן חסומות ולכן מתכנסות, ואחר כך שבהכרח לאותו הגבול. --ארז שיינר 13:55, 29 בינואר 2011 (IST)
הבנתי אותך. רק לא הצלחתי להוכיח שהתת סדרות חסומות. אפשר עזרה?
הסדרה העולה חייבת להיות קטנה מהסדרה היורדת. אם הן היו עוברות אחת את השנייה, ההפרש בין שני איברים עוקבים לא היה יכול לשאוף לאפס. --ארז שיינר 17:06, 29 בינואר 2011 (IST)
אוקי..

עזרה בשאלה נוספת ממבחן

יהי n טבעי, נניח f מוגדרת וגזירה n פעמים בסביבת 0, ו f0=f'0=f0=..=f^(n-1)(0)=0 (נגזרות ב0)., f^(n)(0)=5. חשב 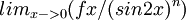lim_{x->0}(fx/(sin2x)^n). תודה מראש

אני מניח שלקחת את השאלה הזו מתוך מבחן של ד"ר הורוביץ (עשיתי אותה לפני כעשר דקות). שים לב לרמז שמופיעה מתחתיה (כאשר x->0 יתקיים ש sinx/x->1), היעזר בו למציאת פונקציה שתהיה במכנה שתהיה נוחה לגזירה, והשתמש בכלל לופיטל n פעמים. מקווה שעזרתי, גל א.
לא הבנתי איך אפשר להשתמש ברמז כדי לפתור את התרגיל- גזרתי את הפונקציה עם לופיטל N פעמים ואף פעם לא היה "x" - רק סינוס, קוסינוס ודברים שקשורים לn. לא הבנתי מה זה אומר למה התכוונת כשאמרת להיעזר בו כדי למצוא פונקציה במכנה נוחה לגזירה.
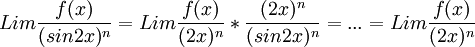Lim\frac{f(x)}{(sin2x)^n}=Lim\frac{f(x)}{(2x)^n}*\frac{(2x)^n}{(sin2x)^n}=...=Lim\frac{f(x)}{(2x)^n} כל הגבולות כאשר איקס שואף לאפס. כעת הפונקציה במכנה "נוחה לגזירה". מה הנגזרת ה-nית שלה? הפעל את כלל לופיטל עבור הנגזרת ה-nית, קבל מסקנה עבור הנגזרת ה-(n-1) והפעל את הכלל שוב ושוב עד שתקבל מסקנה על הפונקציה המקורית. מקווה שעזרתי, גל א.
נראה לי שהבנתי. האם הפתרון הוא 5 חלקי N עצרת כפול 2 בחזקת N?
אכן.

רציפות במ"ש

מישהו יכול לעזור לי למצוא שתי סדרות כדי להפריך רציפות במ"ש של פונקציות xsinx xcosx?

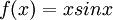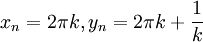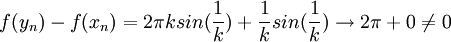f(x)=xsinx וx_n=2\pi k, y_n=2\pi k + \frac{1}{k}. אזי f(y_n)-f(x_n)=2\pi k sin(\frac{1}{k}) + \frac{1}{k}sin(\frac{1}{k}) \rightarrow 2\pi + 0 \neq 0 --ארז שיינר 17:11, 29 בינואר 2011 (IST)

קירוב ליניארי

היי ארז,

באחד המבחנים ביקשו להגדיר את הקירוב הליניארי ולהסביר את חשיבותו....

איך מגדירים זאת בצורה מדוייקת ומה ההסבר הנדרש פה?

תודה!

אני לא בטוח למה הוא מכוון בשאלה, עניתי על זה בתרגיל החזרה. מגדירים את זה בצורה מדוייקת (יש את הנוסחא בדפי התרגיל) ולדעתי ההסבר הוא שניתן כך להעריך פונקציות מבלי להיות מסוגלים לחשב אותן במפורש כאשר אנו כן יודעים לחשב את הפונקציה ואת הנגזרת קרוב לערך המבוקש. --ארז שיינר 16:56, 29 בינואר 2011 (IST)

עזרה בפתרון שאלה

שאלתי את השאלה קודם, אך אני לא בטוח שהפתרון שנתנו לי נכון, לכן אבקש, ארז, אם תוכל, לבדוק שהפתרון שנתנו אכן נכון. הנה השאלה [[1]]. תודה!

לא קראתי את הפתרון הזה, אבל פתרתי את זה בכיתה בשיעור החזרה. אם a_n אינה קושי, אז היא אינה מתכנסת ולכן הגבול החלקי העליון והתחתון שלה שונים, לכן יש לה תת סדרה ששואפת לעליון ותת סדרה ששואפת לתחתון. ניתן לכן לבנות תת סדרה אחרת כך שאיברים הזוגיים שלה יהיו מהראשונה והאיבריים האי זוגיים שלה יהיו מהשנייה. עבור תת סדרה זו, 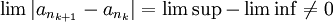\lim |a_{n_{k+1}}-a_{n_k}| = \limsup - \liminf \neq 0 בסתירה. --ארז שיינר 16:52, 29 בינואר 2011 (IST)
תודה.

מישפט היינה בורל

מישהוא יכול ליכתוב אותו בבקשה

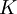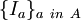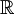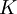"יהי K קטע סגור, ויהיו \{I_a\}_{a\ in\ A} קטעים פתוחים ב-\R כך ש-K מוכל ממש באיחוד של כולם. אזי קיים מספר סופי של קטעים כאלו כך ש-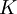K מוכל ממש בתוך האיחוד שלהם". (אני לא הייתי בהרצאה הזו, זה מתוך מחברת שצילמתי ממישהו). מקווה שעזרתי גל א.

תודה פשוט בוויקפדיה זה רשום בצורה קצת פחות פורמלית

אולי יש לכה במיקרה גם את המישפט של בולצאנו ויירשטראס לקבוצות

"תהי S קבוצה המוכלת ממש בממשיים, קבוצה אינסופית אך גם חסומה. אזי קיימת לה נקודת הצטברות". מקווה שעזרתי, גל א.
אגב, אני לומד אצל ד"ר הורוביץ. אם אתה לא לומד אצלו, ייתכן שהמרצה שלך ניסח את זה קצת אחרת, אבל בסופו של דבר זה אותם משפטים.
בולצאנו-ויירשטראס זה לא זה שלכל סדרה חסומה יש תת סדרה מתכנסת?
אני מנחש שהוא מתכוון לגרסא: "לכל קבוצה אינסופית וחסומה יש נקודות הצטברות" --ארז שיינר 19:26, 30 בינואר 2011 (IST)

עזרה בבדיקת היתכנסות הטור

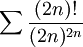
\sum \frac{(2n)!}{(2n)^{2n}}

(לא מתרגל/ת): מתכנס, אני מיד אכתוב למה.
חזרתי:
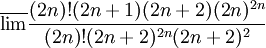
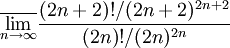
\overline{\lim}\frac{(2n)!(2n+1)(2n+2)(2n)^{2n} }{(2n)!(2n+2)^{2n}(2n+2)^2 } = \overline{\lim_{n\to\infty} }\frac{(2n+2)!/(2n+2)^{2n+2} }{(2n)!/(2n)^{2n} }
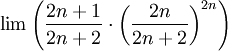
\lim\left(\frac{2n+1}{2n+2}\cdot\left(\frac{2n}{2n+2}\right)^{2n}\right) =
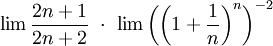
\lim\frac{2n+1}{2n+2}\ \cdot\ \lim\left(\left(1+\frac1n\right)^n\right)^{-2} =
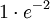
1\cdot e^{-2} =
1 <
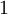
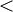
והודות לד'אלמבר הטור (שהוא טור חיובי) מתכנס. \blacksquare

פשש זה בדיוק מה שלא ראיתי החלק של המנה שמיתכנס ל e תודה רבה

בקשה

שלום רב, למישהו יש מושג איך לפתור את שאלה 1א במבחן הזה: http://www.studenteen.org/inf1_exam_blei_2008_a.pdf תודה מראש!

(לא מתרגל/ת): יש לי רעיון מתחכם, אבל יקח לי קצת זמן לכתוב אותו.
יש סיכוי שתכתוב אותו כאן בכל זאת היום או מחר? תודה מראש!
(לא מתרגל/ת): הרעיון הכללי - נוכיח שזה שואף לאינסוף. לשם כך מוכיחים שהטור 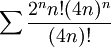\sum \frac{2^n n! (4n)^n}{(4n)!} מתכנס (מבחן ד'אלמבר), לכן 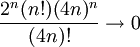\frac{2^n (n!) (4n)^n}{(4n)!}\to0 ולכן (מכיוון שהסדרה הזו חיובית), 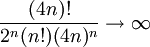\frac{(4n)!}{2^n (n!) (4n)^n}\to\infty. אח"כ, מכיוון ש-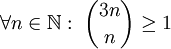\forall n\in\mathbb N:\ \binom{3n}{n}\ge1, מתקיים \forall n\in\mathbb N:\ \sqrt[n]{\binom{3n}{n}}\ge1 ולבסוף נקבל שהסדרה הכללית מתכנסת במובן הרחב לאינסוף. \blacksquare
או, זה יפה ^^

שאלה אלמנטרית

המרצה שלנו כתב בתחילת הקורס: P בריבוע זוגי -> P זוגי. זה כנראה נכון רק כאשר P שלם. יש לזה הוכחה קלה?

גם אני חיפשתי הוכחה עוד מזמן, והגעתי למסקנה שההוכחה היא פשוט של-p בריבוע יש את כל הגורמים של p, פעמיים. אז אם הוא זוגי זה אומר שיש לו את הגורם 2. נניח בשלילה של-p אין את הגורם 2. אבל ל-p בריבוע יש את הגורם 2, לכן חייב להיות ל-p את שורש 2. בסתירה לכך שהוא שלם. לכן יש ל-p את הגורם 2 כלומר הוא זוגי.
זה נכון עבור שלמים, אחרת אין משמעות לזוגי. זה נובע מחומר שהוא לא של הקורס הזה. יש משפט שאומר שאם ראשוני מחלק את ab אז הוא מחלק את a או מחלק את b, לכן אם 2 מחלק את aa=a^2 סימן שהוא מחלק את a. --ארז שיינר 13:08, 30 בינואר 2011 (IST)
ואני הופתעתי שלא מצאתי דרך מתמטית להוכחה אפילו שהמרצה כתב "קל להוכיח ש...".

חתכי דדקינד

לקבוצה של ד"ר שיין תהיה במבחן שאלה על חתכי דדקינד. הבעיה היא שלא היה תרגול בנושא, וגם אין שאלות עם תשובות במיזלר או בכל מקום אחר שבו חיפשתי.

שיין מסר 3 תרגילים בנושא, אבל אין לי מושג לאיזה פתרון הוא מצפה. כלומר, מה הכוונה "שפה של חתכי דדקינד"? אפשר בבקשה לראות פתרון של אחת או כמה מהשאלות הבאות: http://sites.google.com/site/eduardkontorovich/home/%D7%94%D7%9B%D7%A0%D7%94%D7%9C%D7%9E%D7%91%D7%97%D7%9F.pdf?attredirects=0&d=1 בבקשה ותודה רבה מראש!

מצטרף, במיוחד אם אפשר את הפתרון לשאלה 1 (הפתרון היחיד שאני מצאתי הוא "שסדרת החסמים העליונים של An מתכנסת", אבל סדרת החסמים העליונים של An היא בעצם סדרת הממשיים הנוצרים ע"י החתכים, כלומר לא אמרתי כלום בפתרון הזה.)
לי בפתרון חשוב במיוחד לראות את הנימוקים והניסוח, כלומר ה"שפה" של דדקינד. אז למרות שאני חושבת שאני יודעת את התשובה הסופית של 1, יעזור לי מאוד מאוד לראות פתרון מלא של 100 במבחן. אז התשובה, כלומר התנאי, הוא: לכל אפסילון חיובי קיים N כך שלכל n טבעי גדול מ-N, מתקיים שהקבוצה 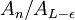A_n/A_{L-\epsilon} מוכלת ב-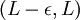(L-\epsilon,L). בעצם שינוי של ההגדרה של ההתכנסות.
התבלבלת, מה זה An/A_L-e?
לא התבלבלתי, זה הקבוצה 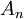A_n בלי הקבוצה 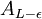A_{L-\epsilon}. תיזכר בסימונים של בדידה.
אוקי.. אבל אני לא רואה איך התנאי פה קשור להתכנסות של סדרת המספרים. אולי תסבירי מה הכוונה פה. אבל בעצם, הרעיון הזה של לקחת את תנאי ההתכנסות למספרים ולהעתיק אותו לחתכים הוא רעיון ממש טוב, נראה לי שהוא יכול לעבוד. בזכות הרעיון שלך פתרתי את זה כך: צריך לעשות קודם כמה הכנות. נגדיר: חתך A הוא "חיובי" אם המס' שמייצר אותו (תמיד קיים) גדול מאפס, או במילים אחרות שכל מספר שקטן nאפס שייך לA (כנ"ל עם שלילי, אי שלילי וכו'). (הערה- כשאני אומר חתך A אני מתכוון לחתך A,A'). כמו כן "A-" הוא החתך שמייצר את המספר הנגדי לA, והרי הוכחנו בכיתה שלכל מספר ממשי יש נגדי ושכל מספר מיוצר ע"י חתך יחיד (כי אם המספר רציונלי, ניקח תמיד חתך מהסוג הראשון, ואם המספר אי רציונלי ניקח חתך מהסוג השלישי), ולכן ההגדרה טובה, ולבסוף נגדיר "|A|" כ-A אם A חיובי וכ- A- אם A שלילי, וב0 ברור. כעת התנאי יהיה שאם לכל אפסילון גדולה E (חתך) חיובית (גדולה מאפס=חיובית כמו שהגדרתי) קיים N כך שלכל n>N מתקיים שהחתך |An-L| מוכל בחתך E. (שוב, החלק השמאלי של החתך), אז סדרת החתכים מתכנסת לL. עכשיו רק צריך להוכיח שזה תנאי הכרחי ומספיק. אולי אנסה בהמשך ואגיד לך אם יש תוצאות..


http://dl.dropbox.com/u/2237179/infi1dedekind.pdf

לא הבנתי אף אחד מהפתרונות שלו ואני גם לא בטוח שהם נכונים.

מי כתב את הפתרון הזה?

זה מה ששיין שלח לתלמידים שלו במייל. תודה שיין, אבל זה כל כך לא בסדר ומלחיץ שלא פתרנו תרגילים כאלו קודם...

בפתרון למבחן של זלצמן 2010

כתוב בפיתרון לשאלה 5.ג ש<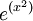e^{(x^2)} רציפה במ"ש.

למה זה נכון?

זה לא נכון, וגם לא רשום שם. רשום שם שהיא רציפה, ובגלל שסינוס גם רציפה, ההרכבה רציפה ומחזורית ולכן ההרכבה רציפה במ"ש. --ארז שיינר 13:12, 30 בינואר 2011 (IST)

כלל לופיטל

כלל לופיטל הוא בחומר של הקבוצה של שיין?

למדנו את זה אז כנראה שכן...

כלל לופיטל

האם אפשר להשתמש בכלל לופיטל כדי למצוא גבולות בקצוות כאשר בודקים רציפות במ"ש של פונקציה?

לדעתי כן, מומלץ לשאול את המרצה או המתרגל בעת המבחן בנוסף. --ארז שיינר 13:24, 30 בינואר 2011 (IST)

מבחני קושי ודלמבר

מבחן קושי הוא עם limsup בשני המקרים (התכנסות והתבדרות) ומבחן דלמבר הוא עם limsup במקרה של התכנסות ו liminf במקרה של התבדרות, או שיש לי טעות? תודה!

אין טעות. תסתכל על ההוכחות שלהם ותבין למה.

חקירת פונקציות, המבחן של ד"ר הורוביץ

צריך לזכור בעל-פה את הסדר של הסעיפים בחקירת פונקציות? (תחום הגדרה ונקודות אי רציפות, האם הפונקציה זוגית/אי-זוגית/לא זה ולא זה, אסימפטוטות, תחומי עלייה+ירידה+נקודות קריטיות, תחומי קעירות+קמירות+נקודות פיתול, טבלת ערכים)
או שזה כתוב במבחן?

הוא אמר שלא בטוח שהוא יכתוב את זה. אבל הוא גם אמר שאין חובה לעשות לפיהסדר שהוא רשם אם כל הסעיפים כלולים. גל א.

ציונים

מספר תעודת הזהות שלי (312491822), ואפילו לא מספר דומה לו, לא מופיע בדף הציונים שפורסם היום. אתם יכולים לבדוק את זה? תודה רבה

יתכן ואתה תיכוניסט? אלו ציונים רק לתלמידים של זלצמן.
כן, תיכוניסט. תודה
הציונים של התיכוניסטים שאדוארד מתרגל מופיעים באתר שלו: sites.google.com/site/eduardkontorovich

איקס בריבוע

איך מוכיחים ש-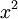x^2 לא רציפה במ"ש? תודה.

(לא מתרגל/ת): ראה פתרון תרגיל 8, שאלה 9.
תודה.

שאלה קלה מדי?

צ"ל או להפריך שאם הטור an מתכנס והטור bn מתבדר אז הטור an+bn מתבדר. לכאורה אפשר להניח בשלילה שהטור an+bn מתכנס, ואז הטור an + הטור bn מתכנס (*), לכן הטור an ועוד הטור bn פחות הטור an = הטור bn מתכנס, בסתירה. אבל ב-(*) הזזנו את המקום של אינסוף איברים, ולכן ההוכחה לא מספיקה. מה לעשות? (ניסיתי לרפד באפסים כמו שכתוב בארכיון 15)

מישהו יודע?

פתרון של הבחינות

הי ארז,

ראשית תודה שהעלת לנו את הפתרון לבחינות כל כך מהר. יתכן ששאלתי לא במקום משום שאני לא לומד אצל זלצמן - אבל מה עם הפתרון לשאלות 3 ו-6 בבחינה שלו? הן היו שאלות של ציטוט משפטים?

אגב, אולי לבחינות של התיכוניסטים כדאי להוסיף הבהרה ששאר השאלות שלא פורסם להן פתרון היו בבחינה של זלצמן (שאלה 1 של הורוביץ = שאלה 1 של זלצמן, שאלה 2 של הורוביץ = שאלה 7 של זלצמן, שאלה 4 של הורוביץ = שאלה 4 של זלצמן, שאלה 5 של הורוביץ = שאלה 2 של זלצמן). כמו כן כדאי להוסיף שהבחינה של ד"ר שיין זהה לבחינה של ד"ר הורוביץ, למעט בשאלה 6 שעסקה בחתכי דדקינד.

כעת שאלה לגבי הפתרונות עצמם: בשאלה 5ג (של זלצמן) כתבת ששורש איקס רציפה בכל הממשיים, אבל זה כמובן לא נכון כי היא מוגדרת רק בממשיים החיוביים. האם יש דרך אחרת להוכיח רציפות במ"ש בסעיף זה בלי להתבסס על טענה זו?

שוב תודה על פרסום הפתרונות (במיוחד עבור המבחן של ד"ר הורוביץ שזה בכלל לא מובן מאליו).

תשובה

שאלה 3 הייתה ציטוט משפטים, שאלה 6 עסקה בנגזרות, ושאלה 8 הייתה להוכיח את משפט קנטור - לא כתבתי להן פתרונות, כמו כן לא כתבתי פתרון לשאלה על חתכי דדיקינד.

לגבי 5ג, לא צריך ששורש איקס יהיה רציף במ"ש על כל הממשיים, אלא רציף במ"ש בתמונה של הפונקציה עליה הוא מורכב - במקרה זה הערך המוחלט ותמונתו 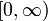[0,\infty) ולכן זה פתרון תקין.

תשובה

אוקי, שוב תודה :-)

מקור: https://math-wiki.com/index.php?title=שיחה:88-132_סמסטר_א%27_תשעא&oldid=9666