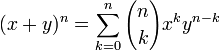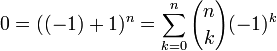הבדלים בין גרסאות בדף "קומבינטוריקה והסתברות - ארז שיינר"
מתוך Math-Wiki
(←נוסחאות הבחירה) |
(←חומר עזר) |
||
| (7 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| + | [[88-165 מבוא להסתברות וסטטיסטיקה]] | ||
| + | |||
=קומבינטוריקה= | =קומבינטוריקה= | ||
[https://youtube.com/playlist?list=PLHinTfsAOC-vv3Av3N4vgwH83TxNZCzBm פלייליסט של כל הסרטונים בקומבינטוריקה] | [https://youtube.com/playlist?list=PLHinTfsAOC-vv3Av3N4vgwH83TxNZCzBm פלייליסט של כל הסרטונים בקומבינטוריקה] | ||
| + | |||
| + | ==חומר עזר== | ||
| + | |||
| + | *[[88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 9|תרגילים בארבעת נוסחאות הבחירה]] | ||
| + | *[[מדיה:11BdidaHadahaBG.pdf|עקרון ההכלה וההדחה]] | ||
==נוסחאות הבחירה== | ==נוסחאות הבחירה== | ||
| שורה 15: | שורה 22: | ||
| − | === | + | ===בחירה עם סדר ועם חזרה=== |
| + | |||
| + | *עם סדר עם חזרה: <math>n^k</math> | ||
*בחירה k פעמים מתוך n אפשרויות עם משמעות לסדר הבחירה ועם חזרות על הבחירה מוגדרת כפונקציה מקבוצת הבחירות אל קבוצת האפשרויות: | *בחירה k פעמים מתוך n אפשרויות עם משמעות לסדר הבחירה ועם חזרות על הבחירה מוגדרת כפונקציה מקבוצת הבחירות אל קבוצת האפשרויות: | ||
| שורה 21: | שורה 30: | ||
| − | + | <videoflash>QBhy3wU9Kro</videoflash> | |
| − | + | ||
| − | <videoflash> | + | ===בחירה עם סדר ובלי חזרה=== |
| + | |||
| + | *עם סדר בלי חזרה: <math>\frac{n!}{(n-k)!}</math> | ||
| + | |||
| + | |||
| + | <videoflash>HLgeJgiCTnY</videoflash> | ||
| + | |||
| + | |||
| + | |||
| + | ===בחירה בלי סדר ובלי חזרה=== | ||
| + | |||
| + | *בלי סדר בלי חזרה: <math>{n\choose k}=\frac{n!}{k!(n-k)!}</math> | ||
| + | |||
| + | <videoflash>RM_NceMarr8</videoflash> | ||
| + | |||
| + | |||
| + | ===בחירה בלי סדר ועם חזרה=== | ||
| + | |||
| + | *בלי סדר עם חזרה: <math>{n-1+k\choose k}={n-1+k\choose n-1}=\frac{(n-1+k)!}{k!(n-1)!}</math> | ||
| + | |||
| + | <videoflash>7QF0-TBDm88</videoflash> | ||
==הבינום של ניוטון ומקדמים מוליטינומיים== | ==הבינום של ניוטון ומקדמים מוליטינומיים== | ||
| + | |||
| + | ===הבינום של ניוטון=== | ||
| + | |||
| + | *<math>(x+y)^n=\sum_{k=0}^n {n\choose k}x^ky^{n-k}</math> | ||
| + | |||
| + | |||
| + | *כמות תתי הקבוצות בגודל זוגי שווה לכמות תתי הקבוצות בגודל אי זוגי כי- | ||
| + | **<math>0=((-1)+1)^n=\sum_{k=0}^n {n\choose k}(-1)^k</math> | ||
| + | |||
| + | |||
| + | <videoflash>aU8xpQHt4MM</videoflash> | ||
| + | |||
==חלוקה למקרים והכלה והדחה== | ==חלוקה למקרים והכלה והדחה== | ||
| שורה 42: | שורה 82: | ||
=הסתברות= | =הסתברות= | ||
| + | מאמר המציג פרדוקסים נחמדים בהסתברות: | ||
| + | |||
| + | [https://www.clear.rice.edu/comp280/10spring/class/19/Teasers.pdf Bar-Hillel, Maya, and Ruma Falk. "Some teasers concerning conditional probabilities."] | ||
גרסה אחרונה מ־18:18, 25 בדצמבר 2023
88-165 מבוא להסתברות וסטטיסטיקה
תוכן עניינים
קומבינטוריקה
פלייליסט של כל הסרטונים בקומבינטוריקה
חומר עזר
נוסחאות הבחירה
מבוא לנוסחאות הבחירה ודוגמא
- kמה פעמים מתוך nה?
בחירה עם סדר ועם חזרה
- עם סדר עם חזרה:
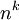
- בחירה k פעמים מתוך n אפשרויות עם משמעות לסדר הבחירה ועם חזרות על הבחירה מוגדרת כפונקציה מקבוצת הבחירות אל קבוצת האפשרויות:
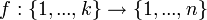
בחירה עם סדר ובלי חזרה
- עם סדר בלי חזרה:
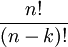
בחירה בלי סדר ובלי חזרה
- בלי סדר בלי חזרה:
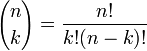
בחירה בלי סדר ועם חזרה
- בלי סדר עם חזרה:
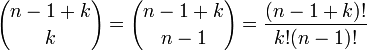
הבינום של ניוטון ומקדמים מוליטינומיים
הבינום של ניוטון
- כמות תתי הקבוצות בגודל זוגי שווה לכמות תתי הקבוצות בגודל אי זוגי כי-
חלוקה למקרים והכלה והדחה
נוסחאות נסיגה
תיאור בעיות באמצעות נוסחאות נסיגה
מעבר מנוסחאת נסיגה לנוסחא מפורשת
פתרון נוסחאת נסיגה הומוגנית
מציאת פתרון פרטי לנוסחאת נסיגה אי הומוגנית
הסתברות
מאמר המציג פרדוקסים נחמדים בהסתברות:
Bar-Hillel, Maya, and Ruma Falk. "Some teasers concerning conditional probabilities."