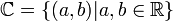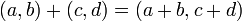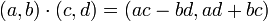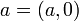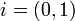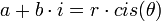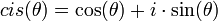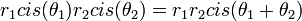הבדלים בין גרסאות בדף "אלגברה לינארית - ארז שיינר"
מתוך Math-Wiki
(←הגדרת המספרים המרוכבים) |
(←שדה המרוכבים) |
||
| שורה 47: | שורה 47: | ||
<videoflash>aDPMK03MCLg</videoflash> | <videoflash>aDPMK03MCLg</videoflash> | ||
| + | |||
| + | ====צורה קרטזית וצורה קוטבית (פולרית)==== | ||
| + | |||
| + | *<math>a+b\cdot i = r\cdot cis(\theta)</math> | ||
| + | *<math>cis(\theta)=\cos(\theta)+i\cdot \sin(\theta)</math> | ||
| + | |||
| + | *<math>r=\sqrt{a^2+b^2}</math> | ||
| + | *עבור הזוית נחלק למקרים: | ||
| + | **אם <math>a>0</math> אזי <math>\theta=arctan\left(\frac{b}{a}\right)</math> | ||
| + | **אם <math>a=0</math> וגם <math>b>0</math> אזי <math>\theta=\frac{\pi}{2}</math> | ||
| + | **אם <math>a=0</math> וגם <math>b<0</math> אזי <math>\theta=\frac{-\pi}{2}</math> | ||
| + | **אם <math>a<0</math> אזי <math>\theta=arctan\left(\frac{b}{a}\right)+\pi</math> | ||
| + | |||
| + | |||
| + | <videoflash>3GOI4vdKv4w</videoflash> | ||
| + | |||
| + | |||
| + | *<math>r_1 cis(\theta_1)r_2 cis(\theta_2)=r_1r_2cis(\theta_1+\theta_2)</math> | ||
| + | |||
| + | |||
| + | <videoflash>kmoxv6cTI24</videoflash> | ||
| + | |||
| − | |||
*דה-מואבר ומציאת שורשים. | *דה-מואבר ומציאת שורשים. | ||
*צמוד מרוכב ושאר הגדרות, הדגמה ע"י פולינום עם מקדמים ממשיים ושורש מרוכב. | *צמוד מרוכב ושאר הגדרות, הדגמה ע"י פולינום עם מקדמים ממשיים ושורש מרוכב. | ||
גרסה מ־15:04, 18 ביוני 2020
תוכן עניינים
- 1 חומר עזר
- 2 סרטוני ותקציר הרצאות
- 2.1 פרק 1 - שדות
- 2.2 פרק 2- מערכות משוואות לינאריות
- 2.3 פרק 3 - אלגברת מטריצות
- 2.4 פרק 4 - מרחבים וקטוריים
- 2.5 פרק 5 - העתקות לינאריות
- 2.6 פרק 6 - דטרמיננטות
חומר עזר
סרטוני ותקציר הרצאות
פרק 1 - שדות
הגדרה ותכונות של שדה
- שדה הוא קבוצה
 יחד עם שתי פעולות
יחד עם שתי פעולות 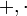 כך שמתקיימות התכונות הבאות:
כך שמתקיימות התכונות הבאות:
- סגירות: לכל
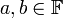 מתקיים כי
מתקיים כי 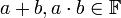
- קומוטטיביות (חילופיות): לכל
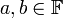 מתקיים כי
מתקיים כי 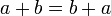 וכן
וכן 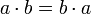
- אסוציאטיביות (קיבוץ): לכל
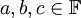 מתקיים כי
מתקיים כי 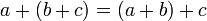 וכן
וכן 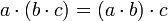
- נייטרליים: קיימים
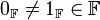 כך שלכל
כך שלכל 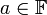 מתקיים כי
מתקיים כי 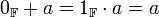
- נגדיים: לכל
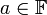 קיים נגדי
קיים נגדי 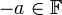 כך ש
כך ש 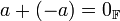
- הופכיים: לכל
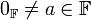 קיים הופכי
קיים הופכי 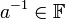 כך ש
כך ש 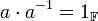
- דיסטריביוטיביות (פילוג): לכל
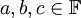 מתקיים כי
מתקיים כי 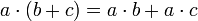
- יהי שדה
 אזי לכל
אזי לכל 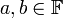 מתקיים כי
מתקיים כי 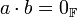 אם ורק אם
אם ורק אם 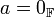 או
או 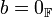
- תכונות נוספות של שדות
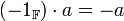
- אם
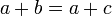 אזי
אזי 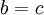
- אם
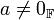 וגם
וגם 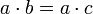 אזי
אזי 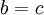
שדות סופיים
שדה המרוכבים
הגדרת המספרים המרוכבים
- נסמן
- נובע כי
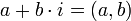
צורה קרטזית וצורה קוטבית (פולרית)
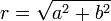
- עבור הזוית נחלק למקרים:
- אם
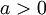 אזי
אזי 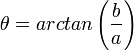
- אם
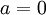 וגם
וגם 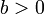 אזי
אזי 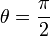
- אם
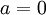 וגם
וגם 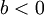 אזי
אזי 
- אם
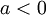 אזי
אזי 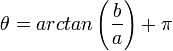
- אם
- דה-מואבר ומציאת שורשים.
- צמוד מרוכב ושאר הגדרות, הדגמה ע"י פולינום עם מקדמים ממשיים ושורש מרוכב.
תרגול
פרק 2- מערכות משוואות לינאריות
הגדרה וייצוג ע"י מטריצות
צורה מדורגת של מטריצה
משתנים חופשיים ותלויים
תרגול
פרק 3 - אלגברת מטריצות
חיבור מטריצות וכפל בסקלר
כפל מטריצות
שחלוף
עקבה
תרגול
מטריצות הופכיות
מטריצות פעולה
תרגול
תרגול בנושא מטריצות הפיכות ומטריצות פעולה
פרק 4 - מרחבים וקטוריים
הגדרה ותכונות של מרחבים וקטוריים
תתי מרחבים
חיתוך, סכום, וסכום ישר של תתי מרחבים
תרגול
פרישה ותלות לינארית
בסיס ומימד
משפט השלישי חינם
תרגול
משפט המימדים
תרגול
הצגה פרמטרית ואלגברית
שלושת מרחבי המטריצה ודרגת מטריצה
תרגול
פרק 5 - העתקות לינאריות
העתקות, הרכבת העתקות, הפיכות העתקות
- מרחב ההעתקות
גרעין ותמונה
משפט הדרגה
תרגול
מטריצה מייצגת העתקה
יחידות הצגה לפי בסיס, קואורדינטות
משפט קיום ויחידות
מטריצת סכום והרכבה
מטריצות מעבר בין בסיסים
תרגול
- תרגול המכיל קואורדינטות ומטריצות מעבר בין בסיסים
- תרגול בנושא מטריצות מייצגות העתקות
- תרגול נוסף בנושא העתקות