שיחה:88-113 סמסטר א' תשעא/קבוצת דיון-עדי ניב
תוכן עניינים
- 1 הוספת שאלה חדשה
- 2 ארכיון
- 3 שאלות
- 3.1 פעולות שורה ועמודהֿ
- 3.2 מרחב וקטורי נוצר סופית
- 3.3 תרגיל 4 שאלה 2
- 3.4 שאלה 1
- 3.5 שאלה 3.18
- 3.6 עזרה במושגים
- 3.7 תרגיל 5? תרגיל 3?
- 3.8 תרגיל 5 שאלה 3.3
- 3.9 שאלה 3.18 א'
- 3.10 3.18 ד'
- 3.11 תרגיל 5 שאלה 3.3 ב
- 3.12 שאלה לעדי
- 3.13 תרגיל 5 שאלה 3.18 סעיף ג
- 3.14 שאלה על 3.18 ד'
- 3.15 שאלה 3.18, סעיפים ה' + ו'
- 3.16 2 דברים לגבי תרגיל 6
- 3.17 שאלה 1 בתרגיל 6
- 3.18 התלבטויות לגבי שילוש
- 3.19 שאלה קצרה ביותר
- 3.20 תרגיל 6
- 3.21 תרגיל 6- שאלה 1
- 3.22 מט' לכסינה~פ"מ
- 3.23 רגולרית?
הוספת שאלה חדשה
הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).
-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן
אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.
ארכיון
שאלות
פעולות שורה ועמודהֿ
רק כדי להיות בטוח- דט' של מט' שהפעלנו עליה פעולות שורה וגם עמודה, שווה לדט' של המטריצה המקורית, נכון?
- (לא מתרגל/ת): לא:
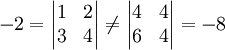 למרות שהכפלנו את השורה הראשונה והעמודה הראשונה ב-2. עם זאת, הדט' של מט' שהפעלנו עליה החלפת שורות וגם עמודות או הוספת מכפלת שורה/עמודה בסקלר - שווה לדט' של המטריצה המקורית (כי הוספת מכפלת שורה/עמודה בסקלר לא משנה את הדטרמיננטה והחלפת שורות k פעמים ב-A ו-k פעמים ב-
למרות שהכפלנו את השורה הראשונה והעמודה הראשונה ב-2. עם זאת, הדט' של מט' שהפעלנו עליה החלפת שורות וגם עמודות או הוספת מכפלת שורה/עמודה בסקלר - שווה לדט' של המטריצה המקורית (כי הוספת מכפלת שורה/עמודה בסקלר לא משנה את הדטרמיננטה והחלפת שורות k פעמים ב-A ו-k פעמים ב- מכפילה את הדט' ב-
מכפילה את הדט' ב-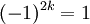 ). אור שחףשיחה 11:39, 8 בנובמבר 2010 (IST)
). אור שחףשיחה 11:39, 8 בנובמבר 2010 (IST)
- גם לא מתרגלת: אבל למדנו שאחרי כפל שורה במטריצה פי a צריך לחלק את הדטרמיננטה ב-a. אז בהנחה שכך זה גם לגבי עמודה, אם כפלת פעמיים פי 2, צריך לחלק ב-4 ואז יצא שיוויון. כך שזו לא דוגמה נגדית כלל. אז אני מצטרפת לשאלה!
- כל שני מספרים שווים עד כדי כפל בקבוע, זה לא אומר שהם שווים באמת. --ארז שיינר 21:46, 8 בנובמבר 2010 (IST)
- (לא מתרגל/ת): תשובה נוספת: כמובן שדט' של מט' שהפעלנו עליה פעולות שורה וגם עמודה ושחילקנו אותה (את הדטרמיננטה) בכל הסקלרים שבהם הכפלנו את השורות והעמודות, שווה לדט' של המטריצה המקורית, אבל זו לא הייתה השאלה. אור שחףשיחה 22:12, 8 בנובמבר 2010 (IST)
- גם לא מתרגלת: אבל למדנו שאחרי כפל שורה במטריצה פי a צריך לחלק את הדטרמיננטה ב-a. אז בהנחה שכך זה גם לגבי עמודה, אם כפלת פעמיים פי 2, צריך לחלק ב-4 ואז יצא שיוויון. כך שזו לא דוגמה נגדית כלל. אז אני מצטרפת לשאלה!
מרחב וקטורי נוצר סופית
מותר לנו להניח שכל המרחבים הוקטורים בתרגילים הם ממימד סופי, גם אם זה לא מצויין מפורשות? אור שחףשיחה 20:05, 8 בנובמבר 2010
עדי: בגדול כן, תהיה ממוקד על שאלה ליתר בטחון.
תרגיל 4 שאלה 2
בתרגיל כתוב למצוא את 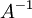 על ידי שימוש בפרוק
על ידי שימוש בפרוק 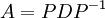 . לא הבנתי מה הכוונה, הדבר היחיד הקשור שמצאתי זה ש-
. לא הבנתי מה הכוונה, הדבר היחיד הקשור שמצאתי זה ש- 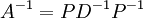 אבל אם כבר מחשבים את
אבל אם כבר מחשבים את 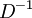 אז פשוט יותר לחשב את
אז פשוט יותר לחשב את 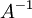 בדרך ה"רגילה" (דירוג (A|I)) וזהו, לא?
בדרך ה"רגילה" (דירוג (A|I)) וזהו, לא?
בעצם מהי הדרך הפשוטה והקצרה ביותר לחשב את 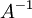 ?
?
- עבור
 הדרך הפשוטה ביותר היא
הדרך הפשוטה ביותר היא 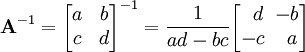
- ועבור
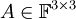 :
: 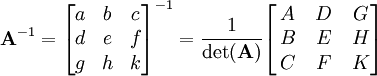
- כאשר

- (מתוך ויקי האנגלית). באופן כללי עדיף לחשב לפי דירוג או adj (מתוך השיטות שכבר למדנו. בוויקיפדיה העברית כתוב שיש שיטות הרבה יותר יעילות, אבל לא נוח ליישם אותן). עם זאת, זה לא רלוונטי כי בתרגיל ביקשו דווקא לפי PDP-1.
- תודה על התשובה. זה בעצם
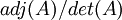 ולמדנו את זה. אני לא רואה היגיון בלחשב את
ולמדנו את זה. אני לא רואה היגיון בלחשב את 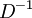 באמצעות שיטה לבחירתי, ואז לחשב את
באמצעות שיטה לבחירתי, ואז לחשב את 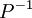 , ואז לכפול שלוש מטריצות, וכל זה במקום חישוב יחיד של
, ואז לכפול שלוש מטריצות, וכל זה במקום חישוב יחיד של 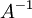 בדרך לבחירתי. למה זה?? אגב, בטוח שהדירוג של (A|I) לא קצר יותר מחישוב
בדרך לבחירתי. למה זה?? אגב, בטוח שהדירוג של (A|I) לא קצר יותר מחישוב 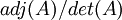 ?
?
- תודה על התשובה. זה בעצם
- מה מיוחד במטריצה D? להפוך אותה לוקח שנייה וחצי ולא צריך שום אלגוריתם. --ארז שיינר 23:45, 8 בנובמבר 2010 (IST)
- אה התבלבלתי בסימון, התכוונתי להפוך את P באמצעות שיטה לבחירתי, ואז להפוך את D, ואז לכפול שלוש מטריצות. החישוב של ההפוכה ל-P הוא מסובך כמו החישוב של ההפוכה של A, לא? אז איפה ההיגיון...
- כי עם P-1 אפשר לחשב גם את A3. אמנם 3 זה לא הרבה, אבל מה אם היו שואלים אותנו על A20? או על A10000? אפילו wolframalpha ויתר. ובלי שום קשר - תשובה?. אור שחףשיחה 00:00, 9 בנובמבר 2010 (IST)
- אופס, בעצם הוא לא ויתר. פשוט אין לו כוח להציג את <צונזר על מנת לשמור על שפיות הדף> אבל ב-100000000 הוא נכנע.
- כי עם P-1 אפשר לחשב גם את A3. אמנם 3 זה לא הרבה, אבל מה אם היו שואלים אותנו על A20? או על A10000? אפילו wolframalpha ויתר. ובלי שום קשר - תשובה?. אור שחףשיחה 00:00, 9 בנובמבר 2010 (IST)
- אה התבלבלתי בסימון, התכוונתי להפוך את P באמצעות שיטה לבחירתי, ואז להפוך את D, ואז לכפול שלוש מטריצות. החישוב של ההפוכה ל-P הוא מסובך כמו החישוב של ההפוכה של A, לא? אז איפה ההיגיון...
- חח טוב השתכנעתי, תודה.
שאלה 1
איך מגיעים מכך ש 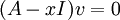 לזה ש A לא הפיכה? תודה!
לזה ש A לא הפיכה? תודה!
- (לא מתרגל/ת): אתה מתכוון
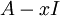 לא הפיכה? A דווקא יכולה להיות הפיכה, למשל אם A=I אז A הפיכה ועבור x=1 מתקיים
לא הפיכה? A דווקא יכולה להיות הפיכה, למשל אם A=I אז A הפיכה ועבור x=1 מתקיים 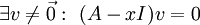 (ולכן יש פתרון לא טריוויאלי ל-(A-xI) ולכן (A-xI) לא הפיכה). ובאותה הזדמנות, כבר 47 שעות לא קיבלתי תשובה פה. אור שחףשיחה 19:11, 10 בנובמבר 2010 (IST)
(ולכן יש פתרון לא טריוויאלי ל-(A-xI) ולכן (A-xI) לא הפיכה). ובאותה הזדמנות, כבר 47 שעות לא קיבלתי תשובה פה. אור שחףשיחה 19:11, 10 בנובמבר 2010 (IST)
- כמו כן, למה כוונתך בשאלה 1? האם כוונתך היא לשאלה הראשונה בתרגול הבית? אם כן באיזה תרגול? או שסתם לשאלה אחת מבין כלל שאלותיך? אבקש, בשמי ושמם של אחרים שלהבא תרשום את מספרה המדויק של השאלה ומאיזה תרגול היא לקוחה, בכדי שנוכל להבין לאיזו "שאלה 1" אתה מתכוון. בכל אופן אם כוונתך היא לשאלה 3.3ב מתרגול 5, הסתמך על הטענה הראשונה באותו הסעיף והוכח בעזרתה את החלק השני של הסעיף. רמז: עבור אילו ערכים של
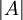 המטריצה לא תהיה הפיכה?
המטריצה לא תהיה הפיכה? - כמו כן - שאלה למתרגלים, מדוע נוצר הפיצול בין קבוצות הדיון? הרי בסופו של דבר אלו אותם השיעורים, ולכן ישאלו אותן השאלות, ובסופו של הדבר אני מאמין שאם מישהו ישאל שאלה בפורום מסוים והיא לא תיענה בו אז הוא ישאל את אותה השאלה גם בפורום השני. בברכה, גל.
- כמו כן, למה כוונתך בשאלה 1? האם כוונתך היא לשאלה הראשונה בתרגול הבית? אם כן באיזה תרגול? או שסתם לשאלה אחת מבין כלל שאלותיך? אבקש, בשמי ושמם של אחרים שלהבא תרשום את מספרה המדויק של השאלה ומאיזה תרגול היא לקוחה, בכדי שנוכל להבין לאיזו "שאלה 1" אתה מתכוון. בכל אופן אם כוונתך היא לשאלה 3.3ב מתרגול 5, הסתמך על הטענה הראשונה באותו הסעיף והוכח בעזרתה את החלק השני של הסעיף. רמז: עבור אילו ערכים של
- כן שאלה 1 מהתרגיל- מן הסתם מהתרגיל הנוכחי, תרגיל 5, ונכון, התכוונתי ל A-xI ולא לA. אפשר עזרה לגבי A-xI? (הסתדרתי בפתרון כללי של התרגיל, אך אני רק צריך עזרה בהוכחת הטענה שבשאלתי). תודה!
- (לא מתרגל/ת): לא הבנתי - יש לך בעיה להוכיח ש-
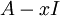 לא הפיכה? כאמור:
לא הפיכה? כאמור: 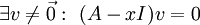 , לכן יש פתרון לא טריוויאלי ל-(A-xI) ולפיכך (A-xI) לא הפיכה, מש"ל. אם זו לא הבעיה - תקן אותי. אור שחףשיחה 21:40, 10 בנובמבר 2010 (IST)
, לכן יש פתרון לא טריוויאלי ל-(A-xI) ולפיכך (A-xI) לא הפיכה, מש"ל. אם זו לא הבעיה - תקן אותי. אור שחףשיחה 21:40, 10 בנובמבר 2010 (IST)
- למה אם יש פתרון לא טריוויאלי אז A-xI לא הפיכה?
- כדאי שתחזור על החומר בלינארית 1, זה היה משפט. בכל אופן, ניתן להוכיח זאת בקלות: נניח בשלילה ש-
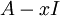 הפיכה, כלומר קיימת
הפיכה, כלומר קיימת 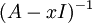 כך ש-
כך ש-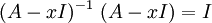 . נכפיל (מימין, כמובן) ב-
. נכפיל (מימין, כמובן) ב-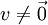 ונקבל
ונקבל
- כדאי שתחזור על החומר בלינארית 1, זה היה משפט. בכל אופן, ניתן להוכיח זאת בקלות: נניח בשלילה ש-
- למה אם יש פתרון לא טריוויאלי אז A-xI לא הפיכה?
- (לא מתרגל/ת): לא הבנתי - יש לך בעיה להוכיח ש-
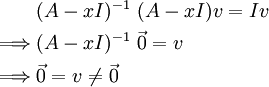
שאלה 3.18
בסעיף א', מה זה אומר (הוכח שהפולינום....) "מאפס את A"?? מה זה מאפס? מאפס כשמציבים משהו? מאפס את הפולינום האופייני של A? ?
תשובה
הצבת מטריצה בפולינום (כמו בלינארית 1). יהי פולינום 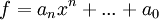 ותהי A מטריצה ריבועית. אזי לפי הגדרה
ותהי A מטריצה ריבועית. אזי לפי הגדרה 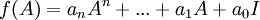 . קל לראות ש
. קל לראות ש 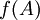 מטריצה ריבועית מאותו גודל כמו A. A מאפסת את f אם המטריצה
מטריצה ריבועית מאותו גודל כמו A. A מאפסת את f אם המטריצה 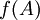 הינה מטריצת האפס. --ארז שיינר 19:23, 11 בנובמבר 2010 (IST)
הינה מטריצת האפס. --ארז שיינר 19:23, 11 בנובמבר 2010 (IST)
- אמרו להוכיח שהפולינום מאפס את A ולא A מאפסת פולינום. ואם הכוונה היא להציב את A בפולינום עם A במקום x, אז הניסוח של השאלה ממש אבל ממש לא ברור
- עדיין לא הבנתי: מה צריך להראות? כי את העובדה ש
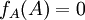 לא צריך להראות בכלל, זה תמיד מתקיים על פי קיילי המילטון. אז מה כן צריך לעשות? תודה
לא צריך להראות בכלל, זה תמיד מתקיים על פי קיילי המילטון. אז מה כן צריך לעשות? תודה
- רשום בשאלה פולינום אופייני? רשומה מטריצה ופולינום, לכן נשאר מה להוכיח, ויש אפילו רמז. --ארז שיינר 05:06, 13 בנובמבר 2010 (IST)
- ברמז מפנים אותך לשאלה שקשורה לפולינום אופייני, אבל הרגע אמרת שאין שום קשר לפולינום אופייני!
- אתה חייב לנסות להבין יותר מאשר להסביר לי... יש קשר לפולינום אופייני, אבל לא נתון שזה פולינום אופייני. לכן אם רוצים לומר את זה צריך להסביר את זה ואז יש תרגיל + פתרון שלו. --ארז שיינר 15:37, 13 בנובמבר 2010 (IST)
- ברמז מפנים אותך לשאלה שקשורה לפולינום אופייני, אבל הרגע אמרת שאין שום קשר לפולינום אופייני!
- רשום בשאלה פולינום אופייני? רשומה מטריצה ופולינום, לכן נשאר מה להוכיח, ויש אפילו רמז. --ארז שיינר 05:06, 13 בנובמבר 2010 (IST)
עזרה במושגים
מהו הפולינום הזה שאפשר להציב בו מטריצות במקום סקלר (איך הוא נקרא\מסומן, התכונות שלו), יש לו קשר לפולינום האופייני? יש לו קשר לפולינום רגיל? ועוד 2 שאלות חשובות:
- איך אפשר למצוא מטריצה שמאפסת פולינום? (האם יש אלגוריתם או דרך לפתרון)?
- מה זה פולינום ש"מאפס את A"?
תודה
- יעזור לקרוא את השאלה שבדיוק נמצאת מעליך.
- אשמח לתשובות לכל השאלות שלא ניענות בשאלה שמעליי (וגם תשובה למה זה"מאפס את A", שאני לא בטוח עדיין מהי התשובה הנכונה). תודה
- רשמתי שם באופן מדוייק כיצד מציבים מטריצה בפולינום (כל פולינום) ומתי אומרים שמטריצה מאפסת פולינום, תקרא היטב. לגבי איך מוצאים מטריצה מאפסת פולינום, זה בדיוק הסעיף הראשון. --ארז שיינר 14:36, 13 בנובמבר 2010 (IST)
- לא, אני יודע מה זה למצוא מטריצה שמאפסת פולינום על פי ההגדרה, אבל איך אפשר למצוא את המטריצה בצורה יותר קלה מההגדרה? (אתה לא מצפה ממני לפתור 5 A בחמישית ועוד 3 A בשלישית וכו', נכון? או לעשות חזקות של מטריצה מסובכת עם מימדים nxn?)
- לא מההגדרה, מהסעיף הראשון שם יש נוסחא מפורשת למטריצה שמאפסת פולינום כלשהו ... --ארז שיינר 15:36, 13 בנובמבר 2010 (IST)
- לא, אני יודע מה זה למצוא מטריצה שמאפסת פולינום על פי ההגדרה, אבל איך אפשר למצוא את המטריצה בצורה יותר קלה מההגדרה? (אתה לא מצפה ממני לפתור 5 A בחמישית ועוד 3 A בשלישית וכו', נכון? או לעשות חזקות של מטריצה מסובכת עם מימדים nxn?)
- רשמתי שם באופן מדוייק כיצד מציבים מטריצה בפולינום (כל פולינום) ומתי אומרים שמטריצה מאפסת פולינום, תקרא היטב. לגבי איך מוצאים מטריצה מאפסת פולינום, זה בדיוק הסעיף הראשון. --ארז שיינר 14:36, 13 בנובמבר 2010 (IST)
- אשמח לתשובות לכל השאלות שלא ניענות בשאלה שמעליי (וגם תשובה למה זה"מאפס את A", שאני לא בטוח עדיין מהי התשובה הנכונה). תודה
- יעזור לקרוא את השאלה שבדיוק נמצאת מעליך.
תרגיל 5? תרגיל 3?
למה בכותרת של תרגיל 5 כתוב תרגיל 3? שלא יצא ששמו בטעות משהו אחר...
תרגיל 5 שאלה 3.3
החלק הראשון של סעיף ב' נכון רק עד כדי 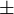 , בתלות בזוגיות n. -לידור.א.- 14:23, 13 בנובמבר 2010 (IST)
עדי:עד כדי +- זה בסדר גמור
, בתלות בזוגיות n. -לידור.א.- 14:23, 13 בנובמבר 2010 (IST)
עדי:עד כדי +- זה בסדר גמור
שאלה 3.18 א'
עשיתי חישוב ישיר של A בריבוע, A בשלישית,..., A בחזקת n, ובסכום a0I+a1A+...+an-1A^n יוצא לי במקום מטריצת האפס, יוצא שהסכום הוא בדיוק 2A^n! זה נכון, או שהיית לי טעות? או שבכלל לא הבנתי את השאלה? קראתי בשאלות מעליי שיש קשר לפולינום האופייני אבל לא הבנתי מהו. פשוט חישבתי ישירות. גם לא הבנתי מה הקשר לתרגיל שברמז. אשמח להסבר מפורט ומובן ככל האפשר. תודה רבה מראש!
תשובה
(לא מתרגל/ת) כנראה הייתה טעות כי הצלחתי להוכיח את המבוקש, דבר שני איך בדיוק אפשר לחשב דבר כזה כאשר n הוא מספר כלשהו? הכיוון הוא יותר פשוט, כמו שנכתב קודם יש קשר לפולינום האופייני, מצא את הפולינום האופייני ולפי קיילי- המילטון A מאפסת אותו, אחרי שלבים אלה ההמשך פשוט.
- חישבתי את זה ע"י חישוב A בריבוע (בעזרת שלוש נקודות כי יש המטריצה היא מגודל n על n), ואז A בשלישית, הבנת העקרון, שלוש נקודות, ואת A בחזקת n. אז הצבת המטריצות בפולינום וזה מה שיצא לי. אם זה לא נכון והפתרון הנכון היחיד הוא עם הפולינום האופייני, אשמח לעזרה בנושא, מכיוון שלא הבנתי את הקשר לפולינום האופייני, ואשמח לתשובה קצת יותר עמוקה מאשר הרמזים הקלושים והעפלוליים שכתובים בשפה מצרית עתיקה ושאותם צריכים מומחים לפענך כדי להבין מה הם אומר- כמו שארז בדרך כלל עונה. תודה
- התבוננו בדף שהעלה לכאן ד"ר צבאן בנושא המטריצה הנלווית. אפשר לומר שדף זה ממש נותן את התשובה לסעיף א... גל א.
עדי: thumbs up
- עדיין לא הבנתי מה צריך לעשות ב-א'.
3.18 ד'
האם מותר להשתמש בטענה שמטריצות עם ערכים עצמיים שווים דומות? אשמח לקבל תשובה בהקדם, תודה לעוזרים
עדי: זה בדיוק מה שאומר הרמז בסוגריים
תודה, הבנתי את הרמז אבל לא ידעתי אם מותר להשתמש בו בלי הוכחה
תרגיל 5 שאלה 3.3 ב
אני חושבת שזה לא נכון שבהכרח 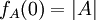 כי הרי
כי הרי 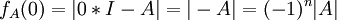 . אז אם n אי זוגי,
. אז אם n אי זוגי, 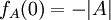 וזה לא בהכרח שווה ל-
וזה לא בהכרח שווה ל-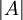 . אז.. איפה טעיתי?
. אז.. איפה טעיתי?
עדי:עד כדי +- זה בסדר גמור
- מה ז"א? ההגדרה של פולינום אופייני היא לא
 אלא
אלא  ??
??
- יש שמגדירים זאת כך
 (כמו שמגדירים בהרצאה) ויש שמגדירים זאת כך
(כמו שמגדירים בהרצאה) ויש שמגדירים זאת כך 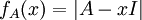 (כמו שמגדירים בחוברת של צבאן). לכן גם "הטעות" כביכול בתרגיל, היא פשות נוסעת מהגדרות שונות. ניתן לשים לב שההבדל בין ההגדרות הוא עד כדי פלוס מינוס, שהרי:
(כמו שמגדירים בחוברת של צבאן). לכן גם "הטעות" כביכול בתרגיל, היא פשות נוסעת מהגדרות שונות. ניתן לשים לב שההבדל בין ההגדרות הוא עד כדי פלוס מינוס, שהרי: 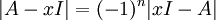 . מקווה שעזרתי, גל א.
. מקווה שעזרתי, גל א.
- יש שמגדירים זאת כך
- העניין הוא שגם בועז צבאן מגדיר את זה
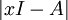 . אבל בקיצור זה לא משנה ואפשר להשתמש באיזו הגדרה מתי שרוצים. תודה על ההסבר.
. אבל בקיצור זה לא משנה ואפשר להשתמש באיזו הגדרה מתי שרוצים. תודה על ההסבר.
- העניין הוא שגם בועז צבאן מגדיר את זה
עדי: לא נכון.הגדרת הפולינום האופייני היא 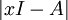 או
או 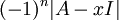 אבל לא
אבל לא 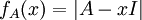 (אלא אם המימד זוגי מין הסתם). כאשר משווים לאפס ע"מ לחפש שורשים סדר החיסור איננו משנה. בכל מקרה מה שאמרה השואלת זה לא שההגדרה של פ"א היא עד כדי +- אלא שהפתרון לסעיף זה הוא נכון עד כדי +-.
(אלא אם המימד זוגי מין הסתם). כאשר משווים לאפס ע"מ לחפש שורשים סדר החיסור איננו משנה. בכל מקרה מה שאמרה השואלת זה לא שההגדרה של פ"א היא עד כדי +- אלא שהפתרון לסעיף זה הוא נכון עד כדי +-.
שאלה לעדי
אני (ועוד כמה) לא נגיע מחר בגלל טיול שנתי בביה"ס, ולכן אנחנו רוצים להגיש את שיעורי הבית היום. זה בסדר אם נשים אותם באחד מהתאים בבניין המתמטיקה? אור שחףשיחה 18:47, 15 בנובמבר 2010 (IST)
- עדי: אני מקווה שלא פיספסתי אתכם. שימו בתא להגשות באיחור בתאים בקומת הכניסה (רשום על זה. אני חושבת שזה 103 אבל לא בטוחה אז תסתכלו על איזה תא רשום). תשלימו את השיעור ועדכנו אם תצטרכו עזרה בהבנתו.
לאוניברסיטה לפי דעתי אפשר להכנס 24/7.מתי המחלקה ננעלת לעומת זאת אין לי מושג...
לא שמתם בסוף?
- אני לא הספקתי, אז הזמנתי שליח (לגבי השאר אני לא יודע). למה את שואלת? זה לא היה בתא? אור שחףשיחה 15:32, 19 בנובמבר 2010 (IST)
תרגיל 5 שאלה 3.18 סעיף ג
מהי האות שהיא המקדם של x^9? היא די דומה לכ' סופית אך זו לא בקבוצת האותיות. -לידור.א.- 22:06, 15 בנובמבר 2010 (IST)
- זו האות ב. אם תתבונן בחוברת של צבאן, שם התרגילים כתובים באותו פונט אבל שלא עבר תאות שונות כגון סריקה והעתקה ולכן רואים יותר טוב, תראה בוודאות שזו ב. גל א.
- זה לא ך' באמת? הרי כתוב שם "תרגיל ארוך". פשוט ערכה שווה לערך של כ'. לא?
- זה בטוח כ' כי כתוב תרגיל ארוך
- זה לא ך' באמת? הרי כתוב שם "תרגיל ארוך". פשוט ערכה שווה לערך של כ'. לא?
שאלה על 3.18 ד'
איך פותרים את זה? יש דרך למצוא מטריצה אך ורק על פי הערכים העצמיים שלה?
עדי:לא תמיד, אבל חשוב מה אנחנו יודעים עליה היות וכל ערכיה העצמיים שונים וכתוצאה מכך מה אנחנו יודעים על כל מט'שדומה לה
- עכשיו התקדמתי והגעתי למשוואה שהפולינום האופייני של המט' החדשה צריכה להיות. הפוילנום האופייני צריך לצאת (x-1)(x^2-2x+2)=0. הבעיה היא עכשיו שלא נראה לי שיכול להיות מטריצה ממשית עם הפולינום האופייני הזה, נראה לי שחלק מאיברי האלכסון חייבים להיות מרוכבים כדי שזה יצא, ואני לא יודע איך פותרים עכשיו..
שאלה 3.18, סעיפים ה' + ו'
בסעיף ה' בשאלה נדרש לחשב את הוקטורים העצמיים של A = companion. אם כל הע"ע העצמיים של A שונים אז היא לכסינה ולכן יש מטריצה מלכסנת שהיא בנויה מן הוקטורים העצמיים שלה בעמודות. לעומת זאת, בסעיף ו', מגדירים את ונדרמונדה להיות כך שהיא transpose של הוקטורים העצמיים שיצאו לי בה', ולכן יוצא כי מה שצריך להוכיח לא נכון. האם יש טעות בתרגיל?
- (לא מתרגל/ת): לא. ביקשו להראות שהמטריצה המתקבלת אלכסונית, לא אלכסונית המתקבלת מליכסון A עם המלכסנת vandermonde. אור שחףשיחה
- הפרכתי את זה עכשיו. לקחתי מטריצה מסדר 2, עם ערכים עצמיים 2 ו-3 ופולינום x^2 -5x + 6. התוצאה של החישוב של מה שהיה צריך להוכיח שיוצא אלכסונית, לא יצא אלכסונית.
עדי:לפי דעתי אתה צודק והוונדרמונד צריך להיות משוחלף. אבדוק בהמשך כשאכתוב פתרונות
- תודה על התשובה. אגב, זה צודק <:
- בפתרונות כתבתם עבור השחלוף של ונדרמונדה. שם זה מתקיים. אני מניח שלא תרדנה לי נקודות אם הפרכתי את הטענה עבור ונדרמונדה הנתונה, נכון?
עדי: לא ירד למי שהפריך את המבוקש או הוכיח עבור שיחלוף. כנ"ל בשאלה עם הפ"א שמציבים בו 0:לא ירד למי שהפריך את המבוקש או הוכיח עבור 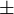 .
.
2 דברים לגבי תרגיל 6
דבר ראשון- הסבר למושגים- מה זה אומר מטריצה אידמפוטנטית? זה כל מטריצה המקיימית A בריבוע שווה A? אם כן, אפשר דוגמה קצרה לאיך A יכולה להיות לא-I? וגם מה זה מטריצה "רגולרית"? (זה לא בסדר שזה לא מוסבר!) ודבר שני, אפשר בבקשה, אלגוריתם מסודר, של איך מוצאים פולינום מינימלי? אני חושב שאמרת (עדי) שתעלי לאתר. תודה רבה!
- (לא מתרגלת) בקשר למט' אידמפוטנטית אני חושבת שכן-כתוב בתרגיל 5.22
- ואם אני לא טועה מטריצה רגולרית זו מטריצה הפיכה
- דוגמאות לאיד': מטריצת האפס, כל מטריצה אלכסונית שעל האלכסון יש בלבד אחדות ואפסים, המטריצה
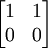 . --ארז שיינר 21:32, 19 בנובמבר 2010 (IST)
. --ארז שיינר 21:32, 19 בנובמבר 2010 (IST) - אשמח גם את האלגוריתם למציאת פולינום מינימלי, אם אפשר. תודה!
- דוגמאות לאיד': מטריצת האפס, כל מטריצה אלכסונית שעל האלכסון יש בלבד אחדות ואפסים, המטריצה
שאלה 1 בתרגיל 6
יצא לי שהפ"א מל"ל ולכן היא ניתנת לשילוש. חישבתי לפי אלגוריתם שהוצג בתרגול (של אוהד, אבל הפורום הזה פעיל) את המט' המשולשית והיא פשוט לא יצאה משולשית. אני בטוחה שעשיתי נכון, בדקתי כמה פעמים. לכן השאלה שלי היא, האם אפשר לכתוב כאן אלגוריתם למציאת מטריצה משולשית דומה? הסתדרתי ><"
התלבטויות לגבי שילוש
יש כמה קטעים לא מובנים לגבי שילוש מטריצה.
נגיד התחלנו במט' שלוש על שלוש וניסינו לשלש אותה. הגענו למט' שקרובה יותר למשולשית, כך שהבלוק 2 על 2 התחתון ימני הוא המט' החדשה שצריך לשלש (1. נכון?), כעת ניסיתי לשלש את המט' 2 על 2 החדשה. הגעתי למט' המשלשת וההופכית שלה, עכשיו מה צריכה להיות המט' ש"אמורה" להיות, אם הצלחנו, משולשית? כלומר (זה די מסובך לכתוב את זה בפורום) אם המט' המקורית היא A, הנסיון לשילוש הראשון שלנו הוביל אותנו ל  , והנסיון לשילוש השני הוביל אותנו למט' השילוש Q ו Q^-1, האם המט' שאמורה להיות משולשת D2 צריכה להיות P-1 כפול Q-1 (בתור בלוק עטוף במט' הזהות) כפול X כפול Q (בלוק בתוך הזהות) כפול P-- אם המבנה הזה נכון (2.), אז מה צריכה להיות (3.) המט' X? המט' A? המט' A' שהיא הבלוק הימני תחתון של המט' D1? תודה
, והנסיון לשילוש השני הוביל אותנו למט' השילוש Q ו Q^-1, האם המט' שאמורה להיות משולשת D2 צריכה להיות P-1 כפול Q-1 (בתור בלוק עטוף במט' הזהות) כפול X כפול Q (בלוק בתוך הזהות) כפול P-- אם המבנה הזה נכון (2.), אז מה צריכה להיות (3.) המט' X? המט' A? המט' A' שהיא הבלוק הימני תחתון של המט' D1? תודה
- (לא מתרגל) הכפל ממנו תקבל את המשולשית הדומה במקרה זה הוא:

- -לידור.א.- 14:07, 20 בנובמבר 2010 (IST)
- 2 דברים- אתה בטוח שה-Q "יותר קרובה" במכפלה למט' המרכזית? כי לפי מה שהעתקתי מהתרגול, עשינו בתרגול ש המט' שדומה למשולשית שווה למכפלה של 5 מט' שהמט' הקרובה יותר לאמצעית היא Q והיותר רחוקה היא P.
- בנוסף, אתה בטוח שהמט' המרכזית היא A? בדקתי עכשיו טוב, ולפי מה שהבנתי המט' המרכזית היא המט' שבשורה ובעמודה הראשונות יש את השורה והעמודה הראשונות של המט' אחרי שניסינו לשלש אותה פעם אחת, ובלוק הימני תחתון יש את המט' המשולשת מסדר 2 על 2 שהגענו אליה אחרי שילוש פעם שניה. בכל מקרה, עשיתי לפי 2 הדברים שאני כתבתי (המט' המרכזית המסובכת ואז Q קרובה יותר וP רחוקה יותר) ויצא לי לא נכון, אחרי שבדקתי את מכפלת 5 המטריצות המכפלה יצאה שונה מA המקורית. אז איפשהו כנראה שטעיתי.
- דוגמא לשילוש אורתוגונאלי. אמנם לא שילוש רגיל, אבל אם נתעלם מפעולת הנרמול זה שילוש רגיל. אולי זה יעזור לכם. --ארז שיינר 14:43, 20 בנובמבר 2010 (IST)
- אנחנו עדיין לא יודעים מה זה אורתוגונאלי, מה זה נרמול, מה הקשר לריבוי גיאומטרי ומה זה קיצורים כמו א"נ, לכן זה לא כל כך מדבר אלינו. אשמח לתשובה פשוטה יותר לגבי המשוואה הסופית שצריכה להיות. בסוף השילוש הרגיל (הראשון שלומדים) יוצא בסוף משוואה A= מכפלה של 5 מטריצות, אשמח לקבל אימות של אילו מטריצות צריכות להיות במכפלה, ואז לראות אולי איפה טעיתי כי המכפלה של המט' כפי שהעתקתי מהתרגול האחרון יצאה לי לא נכונה.
- פשוט תתעלם מהמושגים שאתה לא מכיר, ותחשוב שבחרנו בסיסים רנדומליים כלשהם (במקום בסיס א"נ), האלגוריתם הוא אותו אלגוריתם, ורשום שם אילו מטריצות יש לכפול. --ארז שיינר 15:15, 20 בנובמבר 2010 (IST)
- אנחנו עדיין לא יודעים מה זה אורתוגונאלי, מה זה נרמול, מה הקשר לריבוי גיאומטרי ומה זה קיצורים כמו א"נ, לכן זה לא כל כך מדבר אלינו. אשמח לתשובה פשוטה יותר לגבי המשוואה הסופית שצריכה להיות. בסוף השילוש הרגיל (הראשון שלומדים) יוצא בסוף משוואה A= מכפלה של 5 מטריצות, אשמח לקבל אימות של אילו מטריצות צריכות להיות במכפלה, ואז לראות אולי איפה טעיתי כי המכפלה של המט' כפי שהעתקתי מהתרגול האחרון יצאה לי לא נכונה.
- דוגמא לשילוש אורתוגונאלי. אמנם לא שילוש רגיל, אבל אם נתעלם מפעולת הנרמול זה שילוש רגיל. אולי זה יעזור לכם. --ארז שיינר 14:43, 20 בנובמבר 2010 (IST)
שאלה קצרה ביותר
האם A*X=A גורר ש X=I? תודה
- (לא מתרגל) רק במידה וA הפיכה, אז אתה יכול לכפול בהופכית לה ולקבל I. במקרה אחר זה לא נכון, לדוגמה קח את A להיות מטריצת האפס.-לידור.א.- 13:48, 20 בנובמבר 2010 (IST)
- אוף, זה לא טוב לי- אני צריך להוכיח שמטריצה A היא הפיכה ולכן אני לא יכול להשתמש בזה שהיא הפיכה. אולי אפשר עזרה לגבי איך להוכיח שמט' איד' היא הפיכה? (וגם שהמט' שווה למט' ההפוכה לה)?
- הטענה שמטריצה אידמפוטנטית היא הפיכה אינה נכונה. קח לדוגמה את מטריצת האפס, אידמפוטנטית אבל אינה הפיכה. יותר מזה, יש רק מקרה אחד בו מטריצה אידמפוטנטית היא הפיכה, מטריצת היחידה.-לידור.א.- 15:25, 20 בנובמבר 2010 (IST)
- צודק בהחלט, אז אני תקוע בהוכחת שאלה 2...
- הטענה שמטריצה אידמפוטנטית היא הפיכה אינה נכונה. קח לדוגמה את מטריצת האפס, אידמפוטנטית אבל אינה הפיכה. יותר מזה, יש רק מקרה אחד בו מטריצה אידמפוטנטית היא הפיכה, מטריצת היחידה.-לידור.א.- 15:25, 20 בנובמבר 2010 (IST)
- אוף, זה לא טוב לי- אני צריך להוכיח שמטריצה A היא הפיכה ולכן אני לא יכול להשתמש בזה שהיא הפיכה. אולי אפשר עזרה לגבי איך להוכיח שמט' איד' היא הפיכה? (וגם שהמט' שווה למט' ההפוכה לה)?
תרגיל 6
בשאלה 5.5 ניתבקשנו למצוא פ"מ לפי אלגוריתם שכוויכול למדנו בשיעור אך בשיעור ראינו איך מוצאים פ"מ רק ע"י פ"א!!! מה צריך לעשות???
תרגיל 6- שאלה 1
אני לא מצליח למצוא מט' משולשית עליונה שדומה ל-A. עשיתי לפי האלגוריתם שעשינו בתרגול: מצאתי ע"ע, מצאתי מ"ע השלמתי לבסיס וכך מצאתי את p המשלשת ואת ההופכית שלה אבל אז המכפלה (p^-1)*a*(p) לא נותנת מט' משולשית עליונה.מה עושים?
מט' לכסינה~פ"מ
אם מט' לכסינה (בהתאמה לא לכסינה) מה זה אומר על הפ"מ?
חבר'ה תפתחו את התירגול האחרון עשינו את כל הדברים האלה:
5.5.קיבלתם אלגוריתם למציאת פ"מ
1.P לא אמורה לשלש, אלא רק לאפס מתחת לע"ע המתאימים לה, אח"כ יש להמשיך את התהליך
לכסינה: אז ריבויי שורשי הפ"א הם 1 בפ"מ.
מתי קיבלנו אלגוריתם? בשיעור??? אני מסכם את כל השיעור והדרך היחידה שמצאנו פ"מ היא ע"י פ"א חוץ מזה לא כתבתי וגם אני לא זוכר שקיבלנו אף אלגוריתם במהלך התירגול האחרון
רגולרית?
מישהו יכול לומר לי בבקשה מה זה מט' רגולרית????