הבדלים בין גרסאות בדף "88-113 תשע"ג סמסטר ב' - הודעות"
מתוך Math-Wiki
| (29 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| − | < | + | *רשימת משפטים למבחן |
| + | |||
| + | [[מדיה: mishpatim.jpg|ראה כאן]] | ||
| + | |||
| + | *13/6- השלמה לתירגול | ||
| + | |||
| + | [[מדיה: hashlama.doc|ראה השלמה]] | ||
| + | |||
| + | * מטריצה נורמלית ומשולשית היא אלכסונית: | ||
| + | |||
| + | [[מדיה: diagonal.pdf|ראה הוכחה]] | ||
| + | |||
| + | * להלן הבהרה בנושא ש.ב- תרגילים שיעלו בשבועיים האחרונים של הסמסטר לא יהיו להגשה (כלומר, יעלו עם פתרונות). מתוך 9 התרגילים שכן להגשה ילקחו ה-7 הטובים ביותר. כלומר אם יש תרגיל שאינכם מרוצים מציונו, או שפיספסתם הגשה במהלך הסמסטר, המשיכו להגיש גם את 8 ו-9. | ||
| + | |||
| + | *בדף 7, בעמ' 95 תרגיל 1.4 ב,ג, כתוב לחשב לפי המכפלה הפנימית שמוגדרת ב1.1, הכוונה היא ל 1.3 | ||
| + | |||
| + | *'''שאלה מהכיתה | ||
| + | [[מדיה: pitaron.doc|פיתרון מלא]] | ||
| + | |||
| + | *הוכחת אש"מ לנורמה מושרית מ-מ"פ (מסוף השיעור): | ||
| + | |||
| + | <math>||x+y||^2=||x||^2+2Re<x,y>+||y||^2\leq ||x||^2+2|<x,y>|+||y||^2\leq ||x||^2+2||x||||y||+||y||^2=(||x||+||y||)^2</math> | ||
| + | |||
| + | (האי שיוויון הראשון נכון לכל מרוכב: החלק הממשי והחלק המדומה קטנים או שווים כל אחד מהערך המוחלט. האי שוויון השני הוא קושי-שוורץ). | ||
| + | |||
*תיקון חשוב לתרגיל 2 על ג'ירדון מטריצות | *תיקון חשוב לתרגיל 2 על ג'ירדון מטריצות | ||
[[מדיה: tikun.doc|תיקון לתרגיל 2, תירגול 6]] | [[מדיה: tikun.doc|תיקון לתרגיל 2, תירגול 6]] | ||
| − | + | *טיפ (שקשור לתיקון): למטריצה A משולשית עם 0 על האלכסון, שהרכיבים שונים מ-0 החל מאיזשהו אלכסון מעל הראשי, חזקה של A מעלה באלכסון '''אחד''' (כפי שראינו בכיתה) כאשר האלכסון (אשר החל ממנו רכיבים שונים מאפס) הוא '''אחד''' מעל הראשי (כי | |
| − | (כי <math>(A)_{i,j}\ne 0\ | + | |
| − | + | <math>(A)_{i,j}\ne 0\ \ for\ a_{i,i+1} => A^2_{i,j}\ne0\ \ for\ a_{i,i+1}a_{i+1,i+2}=b_{i,i+2} => A^3\ne 0\ for\ a_{i,i+1}b_{i+1,i+2}=c_{i,i+3} =>...</math>). | |
| − | + | ||
| − | + | באותו אופן, החזקה של A תעלה '''k אלכסונים''' כאשר האלכסון הראשון ששונה מאפס יהיה '''k אלכסונים''' מעל הראשי (כי | |
| + | <math>(A)_{i,j}\ne 0\ \ for\ a_{i,i+k} => A^2_{i,j}\ne0\ \ for\ a_{i,i+k}a_{i+k,i+2k}=b_{i,i+2k} =>...</math>). | ||
*29/4- תרגילים בדוקים שלא נילקחו בכיתה, נמצאים בתיקיה ע"ש הקורס בחדר צילום, בקומת הכניסה של מתמטיקה. | *29/4- תרגילים בדוקים שלא נילקחו בכיתה, נמצאים בתיקיה ע"ש הקורס בחדר צילום, בקומת הכניסה של מתמטיקה. | ||
גרסה אחרונה מ־09:04, 18 ביוני 2013
- רשימת משפטים למבחן
- 13/6- השלמה לתירגול
- מטריצה נורמלית ומשולשית היא אלכסונית:
- להלן הבהרה בנושא ש.ב- תרגילים שיעלו בשבועיים האחרונים של הסמסטר לא יהיו להגשה (כלומר, יעלו עם פתרונות). מתוך 9 התרגילים שכן להגשה ילקחו ה-7 הטובים ביותר. כלומר אם יש תרגיל שאינכם מרוצים מציונו, או שפיספסתם הגשה במהלך הסמסטר, המשיכו להגיש גם את 8 ו-9.
- בדף 7, בעמ' 95 תרגיל 1.4 ב,ג, כתוב לחשב לפי המכפלה הפנימית שמוגדרת ב1.1, הכוונה היא ל 1.3
- שאלה מהכיתה
- הוכחת אש"מ לנורמה מושרית מ-מ"פ (מסוף השיעור):

(האי שיוויון הראשון נכון לכל מרוכב: החלק הממשי והחלק המדומה קטנים או שווים כל אחד מהערך המוחלט. האי שוויון השני הוא קושי-שוורץ).
- תיקון חשוב לתרגיל 2 על ג'ירדון מטריצות
- טיפ (שקשור לתיקון): למטריצה A משולשית עם 0 על האלכסון, שהרכיבים שונים מ-0 החל מאיזשהו אלכסון מעל הראשי, חזקה של A מעלה באלכסון אחד (כפי שראינו בכיתה) כאשר האלכסון (אשר החל ממנו רכיבים שונים מאפס) הוא אחד מעל הראשי (כי
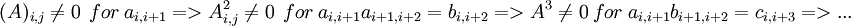 ).
).
באותו אופן, החזקה של A תעלה k אלכסונים כאשר האלכסון הראשון ששונה מאפס יהיה k אלכסונים מעל הראשי (כי
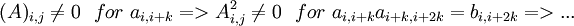 ).
).
- 29/4- תרגילים בדוקים שלא נילקחו בכיתה, נמצאים בתיקיה ע"ש הקורס בחדר צילום, בקומת הכניסה של מתמטיקה.
- חשוב! תיקון להערה מהכיתה: קיים פולינום מתוקן יחיד מדרגה מינימלית (לא מכל דרגה) אשר מאפס את A.
- נא להתעדכן בהערה על תרגיל 4 ובתאריכי ההגשה החדשים.
- יום שני, 8/4/2013: יתקיים תירגול לכולם בזמן ההרצאה (14:00-16:00), במקום התירגולים של אותו יום.
- למגישים באיחור בתאים, נא לציין מחלקה.