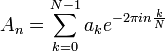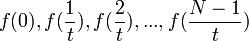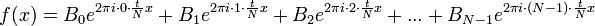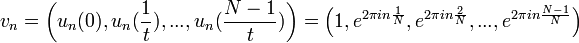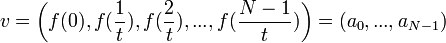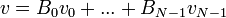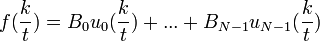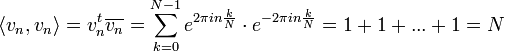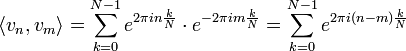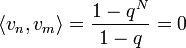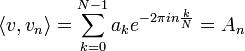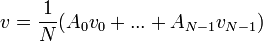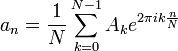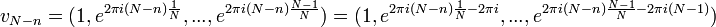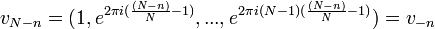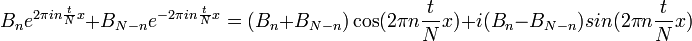הבדלים בין גרסאות בדף "אנליזת פורייה - ארז שיינר"
מתוך Math-Wiki
(←הרצאה 4 - התכנסות במ"ש ושיוויון פרסבל) |
(←תקציר ההרצאות) |
||
| (127 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| + | [[קטגוריה:מערכי לימוד]] | ||
=מבחנים לדוגמא= | =מבחנים לדוגמא= | ||
| + | *[[מדיה:20ForierTestA.pdf|מועד א' תש"ף]] | ||
| + | **[[מדיה:20ForierTestASol.pdf|פתרונות סופיים למועד א' תש"ף]] | ||
| + | *[[מדיה:20ForierTestB.pdf|מועד ב' תש"ף]] | ||
| + | *[[מדיה:19ForierExmplTest.pdf|מבחן לדוגמא תשע"ט]] | ||
| + | **[[מדיה:19ForierExmplTestSol.pdf|פתרון מבחן לדוגמא תשע"ט]] | ||
| + | *[[מדיה:19ForierTestA.pdf|מועד א' תשע"ט]] | ||
| + | **[[מדיה:19ForierTestASol.pdf|פתרון חלקי מאד מועד א' תשע"ט]] | ||
| + | *[[מדיה:19ForierTestB.pdf|מועד ב' תשע"ט]] | ||
| + | **[[מדיה:19ForierTestBSol.pdf|פתרון מועד ב' תשע"ט]] | ||
=תקציר ההרצאות= | =תקציר ההרצאות= | ||
| − | *ההרצאות מבוססות בחלקן על הספר המצויין [ | + | *ההרצאות מבוססות בחלקן על הספר המצויין [https://samyzaf.com/technion/fourier/fourier.pdf 'טורי פוריה' של זעפרני ופינקוס]. |
| + | |||
| + | עוד ספרים מתמטיים בסגנון ניתן למצוא [https://samyzaf.com/ באתר של סמי זערפני]. | ||
| + | |||
==הרצאה 1 - הקדמה ומקדמי פוריה== | ==הרצאה 1 - הקדמה ומקדמי פוריה== | ||
===הקדמה - גלים=== | ===הקדמה - גלים=== | ||
| שורה 64: | שורה 77: | ||
**<math>\frac{1}{\pi}\int_{-\pi}^{\pi}\cos(nx)\cos(nx)dx = \frac{1}{2\pi}\int_{-\pi}^{\pi}(\cos(2nx)+1)dx = \frac{1}{2\pi}\left[\frac{1}{2n}\sin(2nx)+x\right]_{-\pi}^{\pi}=1 </math> | **<math>\frac{1}{\pi}\int_{-\pi}^{\pi}\cos(nx)\cos(nx)dx = \frac{1}{2\pi}\int_{-\pi}^{\pi}(\cos(2nx)+1)dx = \frac{1}{2\pi}\left[\frac{1}{2n}\sin(2nx)+x\right]_{-\pi}^{\pi}=1 </math> | ||
*עבור <math>n\neq k \in \mathbb{N}</math> נקבל: | *עבור <math>n\neq k \in \mathbb{N}</math> נקבל: | ||
| − | **<math>\int_{-\pi}^{\pi}\cos(nx)\cos(kx)dx = \frac{1}{2}\int_{-\pi}^{\pi}(\cos((n+k)x)+\cos((n-k)x))dx = \frac{1}{2}\left[\frac{\sin((n | + | **<math>\int_{-\pi}^{\pi}\cos(nx)\cos(kx)dx = \frac{1}{2}\int_{-\pi}^{\pi}(\cos((n+k)x)+\cos((n-k)x))dx = \frac{1}{2}\left[\frac{\sin((n+k)x)}{n+k}+\frac{\sin((n-k)x)}{n-k}\right]_{-\pi}^{\pi}=0</math> |
**שימו לב כי השתמשנו כאן בעובדה ש<math>n-k,n+k\neq 0</math>. | **שימו לב כי השתמשנו כאן בעובדה ש<math>n-k,n+k\neq 0</math>. | ||
*עבור <math>n,k\in \mathbb{N}</math> נקבל: | *עבור <math>n,k\in \mathbb{N}</math> נקבל: | ||
| שורה 71: | שורה 84: | ||
**<math>\frac{1}{\pi}\int_{-\pi}^{\pi}\cos(0)\cos(0)dx=\frac{1}{\pi}\int_{-\pi}^{\pi}1dx=2</math> | **<math>\frac{1}{\pi}\int_{-\pi}^{\pi}\cos(0)\cos(0)dx=\frac{1}{\pi}\int_{-\pi}^{\pi}1dx=2</math> | ||
*שימו לב שכאשר מציבים 0 בsin מקבלים אפס, ולכן אין צורך בבדיקה הזו. | *שימו לב שכאשר מציבים 0 בsin מקבלים אפס, ולכן אין צורך בבדיקה הזו. | ||
| + | *כמו כן קל לחשב <math>\int_{-\pi}^{\pi} \sin(x)dx = \int_{-\pi}^{\pi} \cos(x)dx=0</math> | ||
*הערה חשובה: | *הערה חשובה: | ||
**למעשה כלל החישובים שעשינו לעיל מוכיחים שהקבוצה <math>\{\frac{1}{\sqrt{2}},sin(x),cos(x),sin(2x),cos(2x),...\}</math> מהווה קבוצה אורתונורמלית לפי המכפלה הפנימית <math>\langle f,g\rangle=\frac{1}{\pi}\int_{-\pi}^{\pi}(f\cdot g) dx</math> | **למעשה כלל החישובים שעשינו לעיל מוכיחים שהקבוצה <math>\{\frac{1}{\sqrt{2}},sin(x),cos(x),sin(2x),cos(2x),...\}</math> מהווה קבוצה אורתונורמלית לפי המכפלה הפנימית <math>\langle f,g\rangle=\frac{1}{\pi}\int_{-\pi}^{\pi}(f\cdot g) dx</math> | ||
| − | |||
====מקדמי הטור==== | ====מקדמי הטור==== | ||
| שורה 214: | שורה 227: | ||
**נגדיר את שתי הפונקציות <math>h_s(t)=\begin{cases}g(t)\sin(\frac{t}{2}) & 0\leq t\leq \pi \\ 0 & -\pi\leq t <0\end{cases}</math> ו <math>h_c(t)=\begin{cases}g(t)\cos(\frac{t}{2}) & 0\leq t\leq \pi \\ 0 & -\pi\leq t <0\end{cases}</math> | **נגדיר את שתי הפונקציות <math>h_s(t)=\begin{cases}g(t)\sin(\frac{t}{2}) & 0\leq t\leq \pi \\ 0 & -\pi\leq t <0\end{cases}</math> ו <math>h_c(t)=\begin{cases}g(t)\cos(\frac{t}{2}) & 0\leq t\leq \pi \\ 0 & -\pi\leq t <0\end{cases}</math> | ||
**קל לראות כי שתי הפונקציות רציפות למקוטעין. לכן פרט לשינוי במספר סופי של נקודות שלא משפיע על האינטגרל, ניתן להניח כי <math>h_c,h_s\in E</math>. | **קל לראות כי שתי הפונקציות רציפות למקוטעין. לכן פרט לשינוי במספר סופי של נקודות שלא משפיע על האינטגרל, ניתן להניח כי <math>h_c,h_s\in E</math>. | ||
| − | **ביחד נקבל כי <math>\int_{0}^\pi g(t)\sin\left(\left(n+\frac{1}{2}\right)t\right)dt = \int_{-\pi}^\pi h_c(t)sin(nt)dt + \int_{-\pi}^\pi h_s(t) | + | **ביחד נקבל כי <math>\int_{0}^\pi g(t)\sin\left(\left(n+\frac{1}{2}\right)t\right)dt = \int_{-\pi}^\pi h_c(t)\sin(nt)dt + \int_{-\pi}^\pi h_s(t)\cos(nt)dt \to 0</math> |
===גרעין דיריכלה=== | ===גרעין דיריכלה=== | ||
| − | *גרעין דיריכלה הוא הפונקציה <math>D_n( | + | *גרעין דיריכלה הוא הפונקציה <math>D_n(t)= \frac{\sin\left(\left(n+\frac{1}{2}\right)t\right)}{2\sin(\frac{t}{2})}</math> |
| − | *טענה: <math>D_n( | + | *טענה: <math>D_n(t)=\frac{1}{2}+\sum_{k=1}^n \cos(kt)</math> בכל נקודה <math>t\neq 2\pi k</math> |
**הוכחה: | **הוכחה: | ||
**נכפל ב<math>2\sin(\frac{t}{2})</math> ונקבל בצד שמאל: | **נכפל ב<math>2\sin(\frac{t}{2})</math> ונקבל בצד שמאל: | ||
| שורה 270: | שורה 283: | ||
*נחזור לסכומים החלקיים ונבצע הצבה: | *נחזור לסכומים החלקיים ונבצע הצבה: | ||
| − | :<math>S_n = \frac{1}{\pi}\int_{-\pi}^\pi f(t)D_n( | + | :<math>S_n = \frac{1}{\pi}\int_{-\pi}^\pi f(t)D_n(t-x)dt = \{ u=t-x, du=dt\} = \frac{1}{\pi}\int_{-\pi-x}^{\pi-x} f(x+u)D_n(u)du</math> |
:כיוון שגרעין דיריכלה ו<math>f</math> הן מחזוריות, נקבל: | :כיוון שגרעין דיריכלה ו<math>f</math> הן מחזוריות, נקבל: | ||
:<math>S_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x+u)D_n(u)du=\frac{1}{\pi}\int_{-\pi}^{\pi} f(x+t)D_n(t)dt</math> | :<math>S_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x+u)D_n(u)du=\frac{1}{\pi}\int_{-\pi}^{\pi} f(x+t)D_n(t)dt</math> | ||
| שורה 333: | שורה 346: | ||
*כעת נחשב את המקדמים של הסינוסים: | *כעת נחשב את המקדמים של הסינוסים: | ||
| − | :<math>b_n=\langle f,sin(nx)\rangle = \frac{1}{\pi}\int_{\pi}^\pi x\sin(nx)dx =\frac{2}{\pi}\int_{0}^\pi x\sin(nx)dx= \frac{2}{n\pi}\left[-x\cos(nx)\right]_{0}^\pi + \frac{2}{n\pi}\int_{0}^{\pi}\cos(nx)dx = | + | :<math>b_n=\langle f,sin(nx)\rangle = \frac{1}{\pi}\int_{-\pi}^\pi x\sin(nx)dx =\frac{2}{\pi}\int_{0}^\pi x\sin(nx)dx= \frac{2}{n\pi}\left[-x\cos(nx)\right]_{0}^\pi + \frac{2}{n\pi}\int_{0}^{\pi}\cos(nx)dx = |
-\frac{2\pi\cos(\pi n)}{\pi n} = \frac{2(-1)^{n+1}}{n}</math> | -\frac{2\pi\cos(\pi n)}{\pi n} = \frac{2(-1)^{n+1}}{n}</math> | ||
*לכן, בכל נקודת רציפות של f, כלומר בכל נקודה <math>x\neq \pi +2\pi k</math>, מתקיים כי: | *לכן, בכל נקודת רציפות של f, כלומר בכל נקודה <math>x\neq \pi +2\pi k</math>, מתקיים כי: | ||
| שורה 348: | שורה 361: | ||
:<math>\frac{\pi}{2}=\sum_{n=1}^\infty\frac{2}{2n-1}\sin(n\pi-\frac{\pi}{2}) =\sum_{n=1}^\infty\frac{-2}{2n-1}\cos(n\pi) = \sum_{n=1}^\infty\frac{2(-1)^{n+1}}{2n-1} </math> | :<math>\frac{\pi}{2}=\sum_{n=1}^\infty\frac{2}{2n-1}\sin(n\pi-\frac{\pi}{2}) =\sum_{n=1}^\infty\frac{-2}{2n-1}\cos(n\pi) = \sum_{n=1}^\infty\frac{2(-1)^{n+1}}{2n-1} </math> | ||
*שימו לב שהפעם לא קיבלנו טור חדש בזכות פורייה, כיוון שנקבל בדיוק את אותו הטור אם נציב 1 בטור הטיילור של <math>arctan(x)</math>. | *שימו לב שהפעם לא קיבלנו טור חדש בזכות פורייה, כיוון שנקבל בדיוק את אותו הטור אם נציב 1 בטור הטיילור של <math>arctan(x)</math>. | ||
| − | |||
=====דוגמא 2===== | =====דוגמא 2===== | ||
| שורה 394: | שורה 406: | ||
===טור הנגזרת=== | ===טור הנגזרת=== | ||
| − | *תהי <math>f</math> | + | *תהי <math>f</math> רציפה בקטע <math>[-\pi,\pi]</math> כך שהנגזרת שלה <math>f'</math> רציפה למקוטעין בקטע. |
| + | ====שימוש בנוסחאת ניוטון לייבניץ לחישוב האינטגרל המסויים==== | ||
| + | *שימו לב שמותר לנו להשתמש בנוסחאת ניוטון לייבניץ: | ||
| + | **כיוון שהנגזרת רציפה למקוטעין, אפשר להראות בעזרת לופיטל שהנגזרות החד צדדיות בנקודות אי הגזירות של f קיימות. | ||
| + | **בעצם, זה מראה שf גזירה בקטעים סגורים בהם אפשר להפעיל את נוסחאת ניוטון לייבניץ. | ||
| + | **אם נחשב את האינטגרל על הנגזרת בכל הקטעים הסגורים, ערכי f יצטמצמו, פרט לקצוות. | ||
| + | ***לדוגמא: | ||
| + | ***<math>\int_{-1}^1 \frac{x}{|x|}dx = \int_{-1}^0 (-1)dx + \int_{0}^1 (1)dx = (-x)|_{-1}^0+(x)|_0^1 = 0-1 + 1-0 = 1-1</math> | ||
| + | ***כלומר קיבלנו כי <math>\int_{-1}^1 \frac{x}{|x|}dx = (|x|)_{-1}^{1}</math>, כאשר <math>(|x|)' = \frac{x}{|x|}</math> | ||
| + | |||
| + | ====חישוב מקדמי טור הפורייה של הנגזרת==== | ||
*נסמן את מקדמי הפורייה של <math>f</math> ב<math>a_n,b_n</math> | *נסמן את מקדמי הפורייה של <math>f</math> ב<math>a_n,b_n</math> | ||
*נחשב את מקדמי הפורייה של הנגזרת, נסמן אותם ב<math>\alpha_n,\beta_n</math>: | *נחשב את מקדמי הפורייה של הנגזרת, נסמן אותם ב<math>\alpha_n,\beta_n</math>: | ||
| + | |||
:<math>\alpha_0=\frac{1}{\pi}\int_{-\pi}^{\pi}f'(x)dx= \frac{f(\pi)-f(-\pi)}{\pi}</math> | :<math>\alpha_0=\frac{1}{\pi}\int_{-\pi}^{\pi}f'(x)dx= \frac{f(\pi)-f(-\pi)}{\pi}</math> | ||
| − | |||
| שורה 410: | שורה 432: | ||
*כלומר, בתנאים הנתונים, אם טור הפוריה של f הינו: | *כלומר, בתנאים הנתונים, אם טור הפוריה של f הינו: | ||
| − | :<math>f(x) | + | :<math>f(x)\sim\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx)</math> |
*אזי טור הפורייה של הנגזרת הינו: | *אזי טור הפורייה של הנגזרת הינו: | ||
| − | :<math>f'(x) | + | :<math>f'(x)\sim\frac{\alpha_0}{2}+\sum_{n=1}^\infty \left((-1)^n\alpha_0+nb_n\right)\cos(nx)-n\cdot a_n\sin(nx)</math> |
*במקרה המיוחד בו <math>f(-\pi)=f(\pi)</math> מתקיים כי <math>\alpha_0=0</math> ולכן נקבל את טור הפורייה הפשוט: | *במקרה המיוחד בו <math>f(-\pi)=f(\pi)</math> מתקיים כי <math>\alpha_0=0</math> ולכן נקבל את טור הפורייה הפשוט: | ||
| − | :<math>f'(x) | + | :<math>f'(x)\sim\sum_{n=1}^\infty nb_n\cos(nx)-na_n\sin(nx)</math> |
| − | + | ||
====דוגמאות==== | ====דוגמאות==== | ||
| שורה 435: | שורה 456: | ||
*נחלץ את המקדמים ונקבל כי טור הפורייה של <math>\frac{x^3}{3}</math> הוא: | *נחלץ את המקדמים ונקבל כי טור הפורייה של <math>\frac{x^3}{3}</math> הוא: | ||
| − | :<math>\frac{x^3}{3} | + | :<math>\frac{x^3}{3} \sim \sum_{n=1}^\infty \frac{2(-1)^n}{n^3}\left(2-\frac{\pi^2 n^2}{3}\right)\sin(nx)</math> |
| − | + | ||
=====דוגמא 2===== | =====דוגמא 2===== | ||
| שורה 470: | שורה 490: | ||
==הרצאה 4 - התכנסות במ"ש ושיוויון פרסבל== | ==הרצאה 4 - התכנסות במ"ש ושיוויון פרסבל== | ||
===תנאי להתכנסות במ"ש של טור פורייה=== | ===תנאי להתכנסות במ"ש של טור פורייה=== | ||
| − | *תהי <math>f</math> | + | *תהי <math>f</math> רציפה בקטע <math>[-\pi,\pi]</math> המקיימת <math>f(-\pi)=f(\pi)</math>, כך ש <math>f'</math> רציפה למקוטעין. |
*אזי טור הפורייה של <math>f</math> מתכנס אליה במ"ש בכל הממשיים. | *אזי טור הפורייה של <math>f</math> מתכנס אליה במ"ש בכל הממשיים. | ||
| שורה 498: | שורה 518: | ||
*סה"כ קיבלנו כי <math>\sum_{n=1}^\infty \sqrt{|a_n|^2+|b_n|^2}</math> מתכנס. | *סה"כ קיבלנו כי <math>\sum_{n=1}^\infty \sqrt{|a_n|^2+|b_n|^2}</math> מתכנס. | ||
*לכן בוודאי גם הטורים הקטנים יותר <math>\sum_{n=1}^\infty |a_n|</math> ו<math>\sum_{n=1}^\infty |b_n|</math> מתכנסים, כפי שרצינו. | *לכן בוודאי גם הטורים הקטנים יותר <math>\sum_{n=1}^\infty |a_n|</math> ו<math>\sum_{n=1}^\infty |b_n|</math> מתכנסים, כפי שרצינו. | ||
| + | |||
| + | |||
| + | ===שיוויון פרסבל=== | ||
| + | *נביט במערכת האורתונורמלית <math>\{\frac{1}{\sqrt{2}},\cos(x),\sin(x),\cos(2x),\sin(2x),...\}\subseteq E</math>, ותהי <math>f\in E</math>. | ||
| + | *ידוע לנו כי <math>a_0=\langle f,1\rangle</math>, ולכן <math>\frac{a_0}{\sqrt{2}}=\langle f,\frac{1}{\sqrt{2}}\rangle</math> | ||
| + | |||
| + | |||
| + | *נסמן את סדרת הסכומים החלקיים של טור הפורייה המתאים לפונקציה f ב <math>S_n</math>. | ||
| + | *<math>S_n</math> היא ההיטל של <math>f</math> על הקבוצה האורתונורמלית <math>\{\frac{1}{\sqrt{2}},\cos(x),\sin(x),\cos(2x),\sin(2x),...,\cos(nx),\sin(nx)\}</math> | ||
| + | **אכן <math>\langle f,\frac{1}{\sqrt{2}}\rangle \frac{1}{\sqrt{2}} + \sum_{n=1}^\infty \langle f,\cos(nx)\rangle \cos(nx) + \langle f,\sin(nx)\rangle \sin(nx) = \frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx)</math> | ||
| + | |||
| + | |||
| + | *נזכור כי <math>||v||^2=||v-\widetilde{v}||^2+||\widetilde{v}||^2</math> | ||
| + | **לכן <math>||f-S_n||^2=||f||^2-||S_n||^2</math>. | ||
| + | *כמו כן, נזכור כי <math>||\widetilde{v}||^2 = \sum_{i=1}^{n}|\langle v,e_i\rangle|^2</math> | ||
| + | **לכן <math>||S_n||^2 = \frac{|a_0|^2}{2}+\sum_{k=1}^n |a_k|^2+|b_k|^2</math> | ||
| + | |||
| + | |||
| + | *אי שיוויון בסל אומר כי <math>\sum_{i=1}^\infty |\langle v,e_i\rangle|^2 \leq ||v||^2</math> | ||
| + | *כלומר: | ||
| + | :<math>\frac{|a_0|^2}{2}+\sum_{n=1}^\infty |a_n|^2+|b_n|^2 \leq ||f||^2 = \langle f,f\rangle = \frac{1}{\pi}\int_{-\pi}^{\pi} |f(x)|^2dx</math> | ||
| + | *משפט שיוויון פרסבל אומר שבעצם מתקיים שיוויון: | ||
| + | :<math>\frac{1}{\pi}\int_{-\pi}^{\pi} |f(x)|^2dx=\frac{|a_0|^2}{2}+\sum_{n=1}^\infty |a_n|^2+|b_n|^2 </math> | ||
| + | |||
| + | |||
| + | |||
| + | *אם נוכיח ש <math>||f-S_n||^2\to 0</math>, נסיק כי <math>||S_n||^2\to ||f||^2</math> וזהו בדיוק שיוויון פרסבל. | ||
| + | |||
| + | |||
| + | ====הוכחת שיוויון פרסבל כאשר טור הפורייה מתכנס במ"ש==== | ||
| + | |||
| + | *תהי <math>f</math> רציפה בקטע <math>[-\pi,\pi]</math> המקיימת <math>f(-\pi)=f(\pi)</math>, כך שהנגזרת שלה <math>f'</math> רציפה למקוטעין. | ||
| + | *נסמן <math>d_n=\sup_{[-\pi,\pi]}|f-S_n|</math> | ||
| + | *הוכחנו כי טור הפורייה של f מתכנס אליה במ"ש, כלומר <math>d_n\to 0</math>. | ||
| + | *לכן <math>||f-S_n||^2 = \frac{1}{\pi}\int_{-\pi}^{\pi} |f-S_n|^2dx \leq 2d_n^2 \to 0</math> | ||
| + | |||
| + | |||
| + | |||
| + | =====דוגמא===== | ||
| + | *הפונקציה <math>f(x)=x^2</math> מקיימת את דרישות המשפט. | ||
| + | *נזכור כי טור הפורייה שלה הוא: | ||
| + | :<math>\frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4(-1)^n}{n^2}cos(nx)</math> | ||
| + | |||
| + | |||
| + | *לכן לפי שיוויון פרסבל נקבל כי: | ||
| + | :<math>\frac{1}{\pi}\int_{-\pi}^{\pi} x^4dx = \frac{4\pi^4}{18}+\sum_{n=1}^\infty \frac{16}{n^4}</math> | ||
| + | |||
| + | |||
| + | :<math>\frac{2\pi^4}{5}-\frac{4\pi^4}{18} = \sum_{n=1}^\infty \frac{16}{n^4}</math> | ||
| + | |||
| + | |||
| + | *ולכן: | ||
| + | :<math>\sum_{n=1}^\infty \frac{1}{n^4} = \frac{\pi^4}{90}</math> | ||
| + | |||
| + | |||
| + | ====הוכחת שיוויון פרסבל במקרה הכללי==== | ||
| + | |||
| + | |||
| + | *תהי <math>f \in E</math>, אנחנו מעוניינים להוכיח כי <math>||f-S_m||\to 0</math>. | ||
| + | *נבנה סדרת פונקציות <math>f_n</math> רציפות בקטע <math>[-\pi,\pi]</math> המקיימות <math>f_n(-\pi)=f_n(\pi)</math>, כך שהנגזרות שלהן <math>f_n'</math> רציפות למקוטעין, המקיימות: | ||
| + | :<math>||f-f_n||\to 0</math> | ||
| + | |||
| + | |||
| + | *יהי <math>\varepsilon</math>, נבחר <math>n</math> כך ש <math>||f-f_n||< \frac{\varepsilon}{2}</math>. | ||
| + | *נסמן ב<math>T_m</math> את סדרת הסכומים החלקיים של טור הפורייה של <math>f_n</math>. | ||
| + | *ראינו כי <math>\lim_{m\to\infty}||f_n-T_m||=0</math>. | ||
| + | |||
| + | |||
| + | *כיוון שההיטל הוא הוקטור הקרוב ביותר, נקבל: | ||
| + | **<math>||f-S_m||\leq ||f-T_m||</math> | ||
| + | *כמו כן, <math>||f-T_m||\leq ||f-f_n||+||f_n-T_m||</math> | ||
| + | *קיים מקום החל ממנו לכל <math>m</math> מתקיים כי <math>||f_n-T_m||< \frac{\varepsilon}{2}</math>. | ||
| + | *לכן החל ממקום זה <math>||f-S_m||<\varepsilon</math> כפי שרצינו. | ||
| + | |||
| + | |||
| + | =====בניית סדרת הפונקציות===== | ||
| + | |||
| + | *f רציפה למקוטעין, ולכן רציפה במ"ש בכל קטע רציפות. | ||
| + | *לכן ניתן לבחור חלוקה <math>P</math> הכוללת את נקודות אי הרציפות, עם פרמטר חלוקה מספיק קטן כך ש <math>|f(x)-f(c_k)|^2< \frac{\varepsilon}{2\pi}</math> לכל זוג נקודות <math>x,c_k\in [x_{k-1},x_k]</math>. | ||
| + | *נבחר נקודות כלשהן <math>c_k</math> בכל קטע ונביט בפונקצית המדרגות g שבכל תת קטע שווה לקבוע <math>f(c_k)</math>. | ||
| + | *כעת האינטגרל תמיד קטן מסכום הדרבו העליון: | ||
| + | **<math>\int_{-\pi}^{\pi} |f-g|^2dx \leq \sum_{k=1}^n \sup_{[x_{k-1},x_k]}|f(x)-f(c_k)|^2 (x_k-x_{k-1}) \leq \sum_{k=1}^n \frac{\varepsilon}{2\pi}(x_k-x_{k-1}) = \varepsilon</math> | ||
| + | *לכן אפשר לבנות סדרת פונקציות מדרגות כנ"ל <math>g_n</math> כך ש<math>||f-g_n||<\frac{1}{n}</math> | ||
| + | |||
| + | |||
| + | |||
| + | *כעת נגדיר סדרת פונקציות <math>f_n</math> להיות <math>g_n</math>, פרט לשינויים הבאים: | ||
| + | **עבור <math>\delta</math> שנקבע בהמשך, נחבר בקו ישר את הנקודות בקצוות המקטעים <math>[x_k-\delta,x_k]</math>. | ||
| + | **נגדיר <math>f_n(-\pi)=g(\pi)</math>. | ||
| + | **נחבר בקו ישר את הנקודות בקצה הקטע <math>[x_0,x_0+\delta]</math>. | ||
| + | *עבור <math>\delta</math> קטנה מספיק, <math>\int_{-\pi}^{\pi}|f_n-g|^2dx < \frac{1}{n}</math>. | ||
| + | |||
| + | |||
| + | *סה"כ נקבל כי | ||
| + | **<math>f_n</math> מורכבת מקטעים ישרים המחוברים זה לזה, ולכן מדובר בפונקציה רציפה, בעלת נגזרת רציפה למקוטעין. | ||
| + | **<math>f_n(-\pi)=f_n(\pi)</math> | ||
| + | **אכן מתקיים כי <math>||f-f_n||\leq ||f-g||+||g-f_n||\to 0</math> | ||
| + | |||
| + | ===יחידות טור פורייה=== | ||
| + | |||
| + | ====הם ישנן שתי פונקציות שונות בעלות אותו טור פורייה?==== | ||
| + | *תהיינה <math>f,g\in E</math> בעלות אותם מקדמי פורייה. | ||
| + | *אם טורי הפורייה מתכנסים לפונקציה, ברור שזו אותה הפונקציה, אבל אם לא? | ||
| + | |||
| + | |||
| + | *מקדמי הפורייה של <math>f-g</math> הם אפס, ולכן לפי שיוויון פרסבל: | ||
| + | :<math>||f-g||^2=0</math> | ||
| + | *לכן <math>f=g</math>. | ||
| + | |||
| + | *שימו לב שעבור סתם פונקציות רציפות למקוטעין, זה אומר ש<math>f=g</math> פרט למספר סופי של נקודות. | ||
| + | |||
| + | ====האם תתכן פונקציה אחת, בעלת שני טורים טריגונומטריים?==== | ||
| + | *קנטור הוכיח שאם טור טריגונומטרי שווה לאפס בכל הקטע <math>[-\pi,\pi]</math>, אזי כל מקדמי הטור הם אפס. | ||
| + | *יותר מאוחר הוכיחו כי אם הטור מתאפס בכל נקודה בקטע פרט לקבוצה בת מנייה של נקודות, עדיין כל מקדמי הטור הם אפס. | ||
| + | *מנשוב מצא ב1916 טור טריגונומטרי שמתכנס לאפס בכל נקודה פרט לקבוצה ממידה אפס של נקודות, אך '''לא''' כל מקדמי הטור הם אפס. | ||
| + | |||
| + | ==הרצאה 5 - תופעת גיבס, טורי הסינוסים והקוסינוסים== | ||
| + | ===תופעת גיבס=== | ||
| + | *ראינו תנאים בהם טור הפורייה מתכנס במ"ש. | ||
| + | *כעת אנחנו רוצים לחקור מקרים בהם אין התכנסות במ"ש, ונראה כי בהן יש חריגה מיוחדת של סדרת הסכומי החלקיים מן הפונקציה. | ||
| + | |||
| + | |||
| + | *נביט בטור פורייה של הפונקציה x: | ||
| + | :<math>\sum_{n=1}^\infty \frac{2(-1)^{n+1}}{n}\sin(nx)</math> | ||
| + | *נסמן ב<math>S_m</math> את סדרת הסכומים החלקיים של הטור ונביט ב: | ||
| + | :<math>S_m(\pi - \frac{\pi}{m})=\sum_{n=1}^m \frac{2(-1)^{n+1}}{n}\sin(n(\pi - \frac{\pi}{m})) = \sum_{n=1}^m \frac{2}{n}\sin(\frac{n\pi}{m})</math> | ||
| + | *כעת, | ||
| + | :<math>\sum_{n=1}^m \frac{2}{n}\sin(\frac{n\pi}{m}) = 2\sum_{n=1}^m \frac{\sin\left(\frac{n\pi}{m}\right)}{\left(\frac{n\pi}{m}\right)}\frac{\pi}{m}\to 2\int_0^\pi \frac{\sin(x)}{x}dx</math> | ||
| + | *לכן סה"כ השגיאה בקירוב ע"י הסכומים החלקיים בסדרת הנקודות הללו היא: | ||
| + | :<math>\pi-\frac{\pi}{m} - S_m (\pi-\frac{\pi}{m}) \to \pi - 2\int_0^\pi \frac{\sin(x)}{x}dx = \int_0^\pi (1-\frac{2\sin(x)}{x})dx \approx -0.56</math> | ||
| + | *(הערכת האינטגרל נעשית על ידי פיתוח טור הטיילור של הפונקציה, נקבל טור לייבניץ לפיו קל לבצע הערכת שגיאה.) | ||
| + | *כלומר סדרת הסכומים החלקיים עולה משמעותית מעל הפונקציה, כפי שניתן לראות בגרף המצורף. | ||
| + | *אם נחלק את זה בגודל הקפיצה בין הגבולות החד צדדים של ההמשך המחזורי של x בנקודה <math>\pi</math>, נקבל בערך <math>-0.089</math>. | ||
| + | |||
| + | |||
| + | *לא נוכיח זאת, אבל יחס הטעות הזה בנקודות אי הרציפות נשמר באופן כללי עבור פונקציות בE שנגזרתן רציפה למקוטעין, ונקרא 'תופעת גיבס'. | ||
| + | |||
| + | |||
| + | :[[קובץ:gibs_x.png|1000px]] | ||
| + | |||
| + | ===טור הסינוסים וטור הקוסינוסים=== | ||
| + | *עבור פונקציה <math>f</math> הרציפה בקטע <math>[0,\pi]</math> ובעלת נגזרת רציפה למקוטעין, ניתן להשלים אותה לפונקציה <math>f^+</math> הזוגית בקטע <math>[-\pi,\pi]</math>, או ל<math>f^-</math> האי זוגית בקטע <math>[-\pi,\pi]</math>. | ||
| + | |||
| + | |||
| + | *את ההמשך הזוגי אפשר לפתח לטור קוסינוסים, שמתכנס במ"ש בקטע <math>[0,\pi]</math>. זה נקרא '''טור הקוסינוסים''' של הפונקציה <math>f</math>. | ||
| + | *הוכחה: | ||
| + | **<math>f^+</math> רציפה ב<math>[-\pi,\pi]</math>, בעלת נגזרת רציפה למקוטעין, ומתקיים כמובן ש<math>f(-\pi)=f(\pi)</math>. | ||
| + | |||
| + | |||
| + | *את ההמשך האי זוגי אפשר לפתח לטור סינוסים, שמתכנס אל הפונקציה בקטע <math>(0,\pi)</math>. זה נקרא '''טור הסינוסים''' של הפונקציה <math>f</math>. | ||
| + | *אם <math>f(\pi)=f(0)=0</math> אזי טור הסינוסים מתכנס במ"ש בקטע <math>[0,\pi]</math>. | ||
| + | *הוכחה: | ||
| + | **<math>f^-</math> רציפה כיוון ש<math>f(0)=0</math>, ומתקיים כי <math>f(-\pi)=-f(\pi)=0=f(\pi)</math>. | ||
| + | |||
| + | |||
| + | *חישוב המקדמים: | ||
| + | *עבור טור הקוסינוסים: | ||
| + | **<math>a_n=\frac{1}{\pi}\int_{-\pi}^{\pi} f^+\cos(nx) dx = \frac{2}{\pi}\int_{0}^{\pi}f\cos(nx)dx </math> | ||
| + | *עבור טור הסינוסים: | ||
| + | **<math>b_n=\frac{1}{\pi}\int_{-\pi}^{\pi} f^-\cos(nx) dx = \frac{2}{\pi}\int_{0}^{\pi}f\sin(nx)dx </math> | ||
| + | |||
| + | |||
| + | ====דוגמאות==== | ||
| + | |||
| + | *נחשב טור קוסינוסים של <math>e^x</math>: | ||
| + | **<math>a_0 = \frac{2}{\pi}\int_0^{\pi} e^xdx = \frac{2}{\pi}(e^\pi-1)</math> | ||
| + | **<math>a_n = \frac{2}{\pi}\int_0^{\pi} e^x\cos(nx)dx = \frac{2}{\pi}\frac{e^\pi(-1)^n-1}{n^2+1}</math> | ||
| + | **הטור מתכנס במ"ש לפונקציה בקטע <math>[0,\pi]</math>: | ||
| + | :<math>e^x=\frac{e^\pi-1}{\pi}+ \frac{2}{\pi}\sum_{n=1}^\infty \frac{e^\pi(-1)^n-1}{n^2+1}\cos(nx) </math> | ||
| + | *לכן מותר לבצע אינטגרציה איבר איבר, נחשב את <math>\int_0^x</math> בשני הצדדים ונקבל: | ||
| + | :<math>e^x-1 - \frac{e^\pi-1}{\pi}x = \frac{2}{\pi}\sum_{n=1}^\infty \frac{e^\pi(-1)^n-1}{n^3+n}\sin(nx)</math> | ||
| + | |||
| + | |||
| + | *נציב למשל <math>x=0</math> ונקבל את השיוויון: | ||
| + | :<math>\sum_{n=1}^\infty \frac{e^\pi(-1)^n-1}{n^2+1} = \frac{\pi}{2} - \frac{e^\pi-1}{2}</math> | ||
| + | |||
| + | |||
| + | *נחשב טור סינוסים של <math>e^x</math>: | ||
| + | **<math>b_n=\frac{2}{\pi}\int_0^\pi e^x\sin(nx)dx = \frac{2n(1-e^\pi(-1)^n)}{\pi(n^2+1)}</math> | ||
| + | **הטור מתכנס בקטע <math>(0,\pi)</math>: | ||
| + | :<math>e^x=\sum_{n=1}^\infty \frac{2n(1-e^\pi(-1)^n)}{\pi(n^2+1)}\sin(nx) </math> | ||
| + | |||
| + | |||
| + | |||
| + | *נחשב טור סינוסים של <math>f(x)=\pi x - x^2</math>. | ||
| + | *שימו לב: <math>f(0)=f(\pi)=0</math>. | ||
| + | **<math>b_n=\frac{2}{\pi}\int_0^\pi (\pi x-x^2)\sin(nx)dx = \frac{4(1-(-1)^n)}{\pi n^3} </math> | ||
| + | **לכן הטור מתכנס במ"ש בקטע <math>[0,\pi]</math>: | ||
| + | :<math>\pi x - x^2 = \sum_{n=1}^\infty \frac{4(1-(-1)^n)}{\pi n^3} \sin(nx)</math> | ||
| + | *לכן מותר לבצע אינטגרציה איבר איבר, נחשב את <math>\int_0^x</math> בשני הצדדים ונקבל: | ||
| + | :<math>\frac{\pi x^2}{2} - \frac{x^3}{3} = \sum_{n=1}^\infty \frac{4(1-(-1)^n)}{\pi n^4}(-\cos(nx)+1)</math> | ||
| + | *שימו לב שלא מדובר בטור טריגונומטרי. | ||
| + | |||
| + | |||
| + | ==הרצאה 6 - משוואת החום על טבעת, התמרת פורייה== | ||
| + | ===משוואת החום על טבעת=== | ||
| + | *נביט במד"ח החום על מוט עבור הפונקציה <math>u(x,t)</math>: | ||
| + | **<math>u_t-ku_{xx}=0</math> | ||
| + | **<math>u(x,0)=f(x)</math> (תנאי התחלה) | ||
| + | **<math>u(-\pi,t)=u(\pi,t)</math> (תנאי שפה) | ||
| + | **<math>u_x(-\pi,t)=u_x(\pi,t)</math> (תנאי שפה) | ||
| + | **כאשר <math>x\in[-\pi,\pi]</math>, ו<math>t\in[0,\infty)</math> | ||
| + | *על מנת להבין את תנאי השפה, אפשר לחשוב על הבעייה במובן שהמוט הוא מעגלי. | ||
| + | |||
| + | |||
| + | *נחפש פתרון מהצורה <math>u(x,t)=X(x)\cdot T(t)</math>. | ||
| + | *נציב במד"ח את הניחוש, ונקבל: | ||
| + | :<math>X(x)T'(t)=kX''(x)T(t)</math> | ||
| + | *נניח שהצדדים שונים מאפס ונחלק: | ||
| + | :<math>\frac{T'(t)}{kT(t)}=\frac{X''(x)}{X(x)}</math> | ||
| + | *כיוון שכל צד תלוי במשתנה אחר, הדרך היחידה לקבל שיוויון היא אם שני הצדדים קבועים. | ||
| + | *נביט בפתרונות עבור קבוע שלילי: | ||
| + | :<math>\frac{T'(t)}{kT(t)}=\frac{X''(x)}{X(x)}=-\lambda</math> | ||
| + | |||
| + | |||
| + | *כעת נפתור את ה[[מד"ר תקציר הרצאות|מד"ר]]ים בנפרד: | ||
| + | *שימו לב שאנו בוחרים את השמות של הקבועים בצורה מיוחדת לקראת הפתרון בהמשך. | ||
| + | **עבור <math>\lambda=0</math>: | ||
| + | ***<math>X_0(x)=cx+\frac{a_0}{2}</math>, ועל מנת לקיים את תנאי השפה נקבל כי <math>c=0</math> | ||
| + | ***<math>T_0(t)=1</math> (הקבוע יבלע בקבוע של <math>X_0(x)</math>) | ||
| + | |||
| + | **עבור <math>\lambda\neq 0</math>: | ||
| + | ***<math>X= a_{\sqrt{\lambda}} \cos(\sqrt{\lambda}x) + b_{\sqrt{\lambda}} \sin(\sqrt{\lambda}x)</math> | ||
| + | ***<math>T=e^{-k\lambda t}</math> (הקבוע חסר כי הוא יבלע בקבועים האחרים כאשר נכפול ב<math>X(x)</math>) | ||
| + | |||
| + | |||
| + | *ע"י הצבה ניתן לוודא שעבור <math>\lambda=n^2</math> הפונקציות לעיל מקיימות את תנאי השפה. | ||
| + | *גם צירוף לינארי שלהן יהווה פתרון כיוון שהמד"ח הומוגנית ותנאי השפה הומוגניים. | ||
| + | *צירוף לינארי אינסופי יהווה פתרון לבעייה אם טורי הנגזרות יתכנסו במ"ש (ולכן יהיה מותר לגזור איבר איבר). | ||
| + | |||
| + | |||
| + | *לכן אנו מחפשים פתרון כללי מהצורה: | ||
| + | :<math>u(x,t)=T_0(t)X_0(x)+\sum_{n=1}^\infty T_n(t)X_n(x) = \frac{a_0}{2} + \sum_{n=1}^\infty e^{-kn^2 t}(a_n\cos(nx)+b_n\sin(nx))</math> | ||
| + | *כל שנותר לנו לעשות הוא למצוא את הקבועים <math>a_n,b_n</math>. | ||
| + | *נציב כעת בתנאי ההתחלה <math>u(x,0)=f(x)</math> ונקבל בעצם את טור הפורייה: | ||
| + | :<math>f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx)</math> | ||
| + | *אנחנו יכולים לפתור משוואה זו בהנתן שf מקיימת את תנאי משפט דיריכלה. | ||
| + | *מדוע זה יהיה פתרון? | ||
| + | **נזכור שמקדמי הפורייה שואפים לאפס. | ||
| + | **בזכות האקספוננט, טור זה ונגזרותיו אכן יתכנסו במ"ש עבור <math>t\in [a,\infty)</math> לכל <math>a>0</math> ולכל <math>x\in[-\pi,\pi]</math>. | ||
| + | **לכן מותר לגזור איבר איבר, ואכן מדובר בפתרון של המד"ח. | ||
| + | |||
| + | ===התמרת פורייה=== | ||
| + | |||
| + | ====טור פורייה המרוכב==== | ||
| + | *לא קשה לוודא כי <math>\{e^{inx}\}_{n\in\mathbb{Z}}</math> מהווה קבוצה אורתונורמלית בE אם נעדכן מעט את המכפלה הפנימית: | ||
| + | :<math>\langle f,g\rangle = \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)\overline{g(x)}dx</math> | ||
| + | *תהי <math>f\in E</math>, שאלה שעולה באופן טבעי היא האם: | ||
| + | :<math>f=\sum_{n=-\infty}^\infty \langle f,e^{inx}\rangle e^{inx}</math> | ||
| + | *כאשר אנו מגדירים את הסכום ממינוס אינסוף עד אינסוף באופן הבא: | ||
| + | :<math>\sum_{n=-\infty}^\infty u_n = u_0+\sum_{n=1}^\infty (u_n+u_{-n}) </math> | ||
| + | |||
| + | |||
| + | *נסמן את מקדמי פורייה הרגילים ב<math>a_n,b_n</math>. | ||
| + | |||
| + | *נשים לב כי עבור <math>n=0</math> נקבל: | ||
| + | :<math>\langle f,1\rangle = \frac{a_0}{2}</math> | ||
| + | *כעת עבור <math>n>0</math> מתקיים: | ||
| + | :<math>\langle f, e^{inx}\rangle e^{inx}+\langle f, e^{-inx}\rangle e^{-inx} =</math> | ||
| + | :<math>= (\langle f, e^{inx}\rangle+\langle f, e^{-inx}\rangle)\cos(nx) + (\langle f, e^{inx}\rangle-\langle f, e^{-inx}\rangle)i\sin(nx)=</math> | ||
| + | :<math>= 2\langle f, \cos(nx)\rangle \cos(nx) + 2\langle f, i\sin(nx)\rangle i\sin(nx)= </math> | ||
| + | :<math>=a_n\cos(nx)+b_n\sin(nx)</math> | ||
| + | *(שימו לב: הi יצא מהצד הימני של המכפלה הפנימית עם מינוס) | ||
| + | |||
| + | |||
| + | *כלומר, טור פורייה המרוכב הוא בדיוק טור פורייה הרגיל! | ||
| + | |||
| + | ====הכללה לפונקציות שאינן מחזוריות==== | ||
| + | *טורי פורייה עזרו לנו לחקור פונקציות בקטע <math>[-\pi,\pi]</math>. | ||
| + | *בהנתן גל <math>e^{inx}</math>, מצאנו את ה'אמפליטודה' שלו (המקדם): | ||
| + | :<math>\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)e^{-inx}dx</math> | ||
| + | *(שימו לב - המכפלה הפנימית מצמידה את הפונקציה מימין, ולכן קיבלנו <math>-i</math>). | ||
| + | |||
| + | |||
| + | |||
| + | *מחשבה הגיונית היא שאם נרצה לחקור פונקציות בכל הממשיים, עבור גל <math>e^{isx}</math> נמצא את ה'אמפליטודה': | ||
| + | :<math>\mathcal{F}[f](s)=\frac{1}{2\pi}\int_{-\infty}^\infty f(x)e^{-isx}dx</math>. | ||
| + | *כאשר האינטגרל מתכנס, הפונקציה <math>\mathcal{F}[f](s)</math> נקראת '''התמרת פורייה''' של הפונקציה <math>f</math>. | ||
| + | *הערה - המקדם <math>\frac{1}{2\pi}</math> לעיתים אינו מופיע בהגדרת ההתמרה. אנחנו נראה בהמשך שיש לו קשר להתמרה ההפוכה. | ||
| + | |||
| + | |||
| + | *הערות כלליות: | ||
| + | **נסמן בדר"כ את ההתמרה של f ב<math>F(s)=\mathcal{F}(f)(s)</math>. | ||
| + | **<math>F(s)</math> מייצגת את האמפליטודה בכל תדר, ולכן נהוג לומר שהיא מוגדרת ב'מרחב התדר'. | ||
| + | **לעומת זאת, <math>f(x)</math> מייצגת את גובה הפונקציה בכל נקודה בזמן, ונהוג לומר שהיא מוגדרת ב'מרחב הזמן'. | ||
| + | **לכל תדר <math>s</math> יש שני גלים שמייצגים אותו, <math>e^{\pm isx}</math>. | ||
| + | **כפי שלמדנו, באמצעות שני הגלים ניתן לייצג כל 'פאזה'. | ||
| + | |||
| + | |||
| + | *נסמן ב<math>G</math> את אוסף הפונקציות <math>g</math> הרציפות למקוטעין ב<math>\mathbb{R}</math>, עבורן האינטגרל הלא אמיתי מתכנס <math>\int_{-\infty}^\infty|g(x)|dx<\infty</math>. | ||
| + | *לכל <math>f\in G</math> התמרת הפורייה מוגדרת בכל הממשיים. | ||
| + | **הוכחה: | ||
| + | **<math>\int_{-\infty}^\infty|f(x)e^{-isx}|dx = \int_{-\infty}^\infty|f(x)|dx</math> מתכנס. | ||
| + | **כיוון שהאינטגרל המגדיר את <math>F(s)</math> מתכנס בהחלט, הוא מתכנס. | ||
| + | |||
| + | =====דוגמאות===== | ||
| + | *נמצא את <math>\mathcal{F}(f)(s)</math> עבור <math>f(x)=e^{-|x|}</math>. | ||
| + | :<math>2\pi F(s)=\int_{-\infty}^\infty e^{-|x|}e^{-isx}dx = \int_0^\infty e^{-x}e^{-isx}dx + \int_{-\infty}^0 e^{x}e^{-isx}dx=</math> | ||
| + | :<math>=\left[\frac{e^{-x(1+is)}}{-(1+is)}\right]_0^\infty + \left[\frac{e^{x(1-is)}}{1-is}\right]_{-\infty}^0=\frac{1}{1+is} + \frac{1}{1-is} = \frac{2}{1+s^2}</math> | ||
| + | *שימו לב - השתמשנו בעובדה ש<math>e^{isx}</math> חסומה, ואילו <math>e^{-x}\to 0</math> כאשר <math>x\to \infty</math>. | ||
| + | *לכן סה"כ קיבלנו כי <math>\mathcal{F}[e^{-|x|}](s) = \frac{1}{\pi(1+s^2)}</math> | ||
| + | |||
| + | |||
| + | *נמצא את התמרת הפורייה של <math>f(x)=\begin{cases}|x| & |x|\leq \pi \\ 0 & |x|>\pi\end{cases}</math> | ||
| + | :<math>F(s)=\frac{1}{2\pi}\int_{-\infty}^\infty f(x)e^{-isx}dx = \frac{1}{2\pi}\int_{-\pi}^\pi |x|e^{-isx}dx = </math> | ||
| + | :<math>\frac{1}{2\pi}\int_{-\pi}^\pi |x|\cos(sx)dx - \frac{i}{2\pi}\int_{-\pi}^\pi |x|\sin(sx)dx = \frac{1}{\pi}\int_{0}^\pi x\cos(sx)dx = \frac{\sin(s\pi)}{s} + \frac{\cos(s\pi)-1}{s^2\pi}</math> | ||
| + | |||
| + | |||
| + | *שימו לב: חישוב האינטגרל שגוי עבור <math>s=0</math>, ניתן להציבו בנוסחא המקורית של האינטגרל או להשתמש ברציפות ההתמרה, שנלמד בהמשך. | ||
| + | |||
| + | ==הרצאה 7 - תכונות של התמרות פורייה== | ||
| + | ===תכונות ההתמרה=== | ||
| + | *תהי <math>f\in G</math> אזי <math>F(s)=\mathcal{F}[f](s)</math> רציפה במ"ש ב<math>\mathbb{R}</math>. | ||
| + | **הוכחה: | ||
| + | **יהי <math>\varepsilon>0</math>. כיוון ש <math>\int_{-\infty}^{\infty}|f(x)|dx</math> מתכנס, קיים <math>R</math> עבורו <math>\frac{1}{2\pi}\int_{|x|>R}|f(x)|dx <\frac{\varepsilon}{4}</math> | ||
| + | **עבור <math>s_1,s_2</math> מתקיים כי <math>|F(s_1)-F(s_2)|\leq \frac{1}{2\pi}\int_{-\infty}^{\infty}|f(x)(e^{-is_1x}-e^{-is_2x})|dx</math> | ||
| + | **כמובן ש <math>|e^{-is_1x}-e^{-is_2x}|\leq 2</math> ולכן בתחום <math>|x|>R</math> האינטגרל הנ"ל קטן מ<math>\frac{\varepsilon}{2}</math>. | ||
| + | **נותר להוכיח שעבור <math>s_1,s_2</math> מספיק קרובים מתקיים כי <math>\frac{1}{2\pi}\int_{-R}^{R}|f(x)(e^{-is_1x}-e^{-is_2x})|dx<\frac{\varepsilon}{2}</math> | ||
| + | **נראה כי <math>|e^{ix}-e^{iy}|\leq |x-y|</math>. | ||
| + | ***<math>|e^{ix}-e^{iy}|</math> הוא המרחק בין שתי נקודות על מעגל היחידה. | ||
| + | ***<math>|x-y|</math> הוא הזווית בינהן, כלומר אורך הקשת בינהן. | ||
| + | ***אורך הקשת בוודאי גדול או שווה למרחק הישר בין שתי הנקודות. | ||
| + | **לכן <math>|e^{-is_1x}-e^{-is_2x}|\leq |x||s_1-s_2|</math> | ||
| + | **כיוון ש<math>|x|\leq R</math> והפונקציה <math>f</math> חסומה בתחום זה, עבור <math>|s_1-s_2|</math> מספיק קטן נקבל את הדרוש. | ||
| + | |||
| + | |||
| + | *רשימת תכונות נוספות של ההתמרה: | ||
| + | *<math>\mathcal{F}[f+a\cdot g] = \mathcal{F}[f]+a\mathcal{F}[g]</math> | ||
| + | *<math>\mathcal{F}[f](-s) = \overline{\mathcal{F}[f](s)}</math> | ||
| + | *אם <math>f</math> ממשית וזוגית, גם <math>\mathcal{F}[f](s)</math> ממשית וזוגית. | ||
| + | |||
| + | |||
| + | *הזזה במרחב הזמן: | ||
| + | *אם <math>g(x)=f(ax+b)</math>, אזי <math>\mathcal{F}(g)(s) = \frac{1}{|a|}e^{\frac{isb}{a}}\mathcal{F}[f](\frac{s}{a})</math> | ||
| + | *אם <math>a=1</math> אז נקבל שהזזה במרחב הזמן שקולה לסיבוב במרחב התדר (כפל ב<math>e^{isb}</math> משנה את הזוית). | ||
| + | |||
| + | |||
| + | *הזזה במרחב התדר: | ||
| + | *<math>\mathcal{F}[e^{ibx}f(x)](s) = \mathcal{F}[f](s-b)</math> | ||
| + | *באופן דומה, קיבלנו שסיבוב בזמן שקול להזזה בתדר. | ||
| + | |||
| + | |||
| + | *התמרת הנגזרת: | ||
| + | *נניח <math>f,f'\in G</math> ונניח כי <math>f'</math> רציפה ומתקיים כי <math>\lim_{x\to \pm\infty}f(x)=0</math>, אזי: | ||
| + | *<math>\mathcal{F}[f'](s)=is\mathcal{F}[f](s)</math> | ||
| + | **הוכחה: | ||
| + | **<math>\mathcal{F}[f'](s) = \frac{1}{2\pi}\int_{-\infty}^{\infty} f'(x)e^{-isx}dx</math> | ||
| + | **נבצע אינטגרציה בחלקים ונקבל כי | ||
| + | **<math>\mathcal{F}[f'](s) = \frac{1}{2\pi}(fe^{-isx})_{-\infty}^{\infty} + \frac{is}{2\pi} \int_{-\infty}^{\infty} f(x)e^{-isx}dx</math>. | ||
| + | **כיוון ש<math>e^{-isx}</math> חסומה, יחד עם הנתון נובע כי <math>(fe^{-isx})_{-\infty}^{\infty}=0</math>. | ||
| + | **לכן סה"כ קיבלנו כי <math>\mathcal{F}[f'](s)=is\mathcal{F}[f](s)</math> | ||
| + | |||
| + | |||
| + | *נגזרת ההתמרה: | ||
| + | *תהי <math>f\in G</math> רציפה כך ש<math>xf(x)\in G</math> אזי: | ||
| + | *<math>\mathcal{F}[xf(x)](s)=i\frac{d}{ds}\mathcal{F}[f](s)</math> | ||
| + | **הוכחה: | ||
| + | **<math>i\frac{d}{ds}\mathcal{F}[f](s) = i \frac{d}{ds} \frac{1}{2\pi}\int_{-\infty}^{\infty} f(x)e^{-isx}dx = \frac{i}{2\pi}\int_{-\infty}^{\infty} f(x)\frac{d}{ds}e^{-isx}dx = \frac{-i^2}{2\pi}\int_{-\infty}^{\infty} xf(x)e^{-isx} = \mathcal{F}[xf(x)](s)</math> | ||
| + | **אנחנו צריכים להצדיק את ההכנסה של הנגזרת אל תוך האינטגרל: | ||
| + | ***נסמן <math>F_n(s)=\frac{1}{2\pi}\int_{-n}^{n} f(x)e^{-isx}dx</math> | ||
| + | ***ברור ש<math>F_n(s)\to F(s)</math>, נוכיח שסדרת הנגזרות מתכנסת במ"ש ולכן מתכנסת לנגזרת של <math>F(s)</math>. | ||
| + | ***עבור אינטגרל סופי מותר להחליף את סדר הנגזרת והאינטגרל בזכות פוביני. | ||
| + | ***אכן <math>F_n'(s)</math> מתכנסות במ"ש כיוון שהאינטגרל <math>\int_{-\infty}^\infty |xf(x)|dx</math> מתכנס, והרי <math>|xf(x)e^{-isx}|=|xf(x)|</math> ואכן אינו תלוי בs. | ||
| + | |||
| + | ====דוגמאות==== | ||
| + | |||
| + | *ראינו כי <math>\mathcal{F}[e^{-|x|}](s) = \frac{1}{\pi(1+s^2)}</math> | ||
| + | *לכן על ידי הזזה בזמן נקבל כי: | ||
| + | **<math>\mathcal{F}[e^{-|1-2x|}](s) = \frac{e^{\frac{-is}{2}}}{2\pi (1+(-\frac{s}{2})^2)}</math> | ||
| + | |||
| + | |||
| + | *נסמן <math>F(s)=\mathcal{F}[e^{-x^2}]</math>. | ||
| + | *כעת <math>\mathcal{F}[xe^{-x^2}] = iF'</math> לפי הנוסחא של נגזרת ההתמרה. | ||
| + | *מצד שני, <math>\mathcal{F}[-2xe^{-x^2}] = isF</math> לפי הנוסחא של התמרת הנגזרת. | ||
| + | *ביחד נקבל כי <math>isF = -2iF'</math>, ולכן <math>sF=-2F'</math>. | ||
| + | *נפתור את המד"ר: | ||
| + | **נכפול בגורם אינטגרציה <math>\frac{1}{2}e^{\frac{s^2}{4}}</math> ונקבל <math>(e^{\frac{s^2}{4}}F)'=0</math> | ||
| + | **לכן <math>F=Ce^{-\frac{s^2}{4}}</math> | ||
| + | **נציב <math>s=0</math> | ||
| + | **<math>2\pi C=F(0)=\int_{-\infty}^\infty e^{-x^2}dx </math>, נחשב אינטגרל מפורסם זה בהמשך. | ||
| + | |||
| + | ==הרצאה 8 - התמרה הפוכה== | ||
| + | |||
| + | *בטורי פורייה, מקדמי הפורייה היו האמפליטודות של התדרים, וכאשר סכמנו את הגלים קיבלנו חזרה את הפונקציה לפי משפט דיריכלה. | ||
| + | *כעת התדרים שלנו הם כל הממשיים, ולכן הסכימה שלהם היא בעצם אינטגרל. | ||
| + | *האמפליטודה של כל תדר מרוכב <math>e^{isx}</math> היא התמרת הפורייה <math>F(s)</math>, ולכן אנחנו מצפים לקבל: | ||
| + | **<math>f(x)=\int_{-\infty}^\infty F(s)e^{isx}ds=\mathcal{F}^{-1}[F](x)</math> | ||
| + | |||
| + | |||
| + | |||
| + | *משפט ההתמרה ההפוכה: | ||
| + | **תהי <math>f\in G</math>, אזי בכל נקודה בה קיימות הנגזרות החד צדדיות מתקיים כי: | ||
| + | **<math>\frac{f(x^+)+f(x^-)}{2}=\lim_{n\to\infty}\int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\mathcal{F}[f](s)e^{isx}ds</math> | ||
| + | **שימו לב שהאינטגרל <math>\int_{-\infty}^{\infty}\mathcal{F}[f](s)e^{isx}ds</math> לא חייב להתכנס, אבל אם הוא מתכנס הוא שווה לגבול לעיל. | ||
| + | |||
| + | ===דוגמא=== | ||
| + | |||
| + | *ראינו ש<math>\mathcal{F}[e^{-x^2}] = Ce^{-\frac{s^2}{4}} =\frac{1}{2\pi}\int_{-\infty}^\infty e^{-x^2}e^{-isx}dx</math> | ||
| + | *כיוון ש<math>e^{-x^2}</math> רציפה וגזירה, וכיוון ש <math>e^{-\frac{s^2}{4}}\in G</math> לפי משפט ההתמרה ההפוכה נקבל כי: | ||
| + | **<math>\mathcal{F}^{-1}[Ce^{-\frac{s^2}{4}}](x) = e^{-x^2}</math> | ||
| + | *כלומר <math>e^{-x^2}=\int_{-\infty}^\infty Ce^{-\frac{s^2}{4}}e^{isx}ds </math> | ||
| + | *נציב <math>t=\frac{s}{2}</math> ונקבל: | ||
| + | **<math>e^{-x^2} = 2C\int_{-\infty}^\infty e^{-t^2}e^{-i(-2x)t}dt = 2C\cdot 2\pi Ce^{-\frac{(-2x)^2}{4}}</math> | ||
| + | *ולכן <math>4C^2\pi = 1</math>, ומכאן <math>C=\frac{1}{2\sqrt{\pi}}</math> | ||
| + | |||
| + | |||
| + | *נזכור בנוסף שראינו כי <math>2\pi C = \int_{-\infty}^\infty e^{-x^2}dx</math>. | ||
| + | *לכן נובע כי <math>\int_{-\infty}^\infty e^{-x^2}dx = \sqrt{\pi}</math> | ||
| + | |||
| + | ===דוגמא=== | ||
| + | *נביט ב<math>f(x)=\begin{cases}1 & |x|<1 \\ 0 & |x|>1\end{cases}</math> | ||
| + | *<math>\mathcal{F}[f](s) = \frac{sin(s)}{\pi s}</math> | ||
| + | *<math>\lim \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}} \frac{sin(s)}{\pi s}e^{is}ds = \frac{1}{2}</math> (הצבנו x=1, הנקודה בה f אינה רציפה). | ||
| + | |||
| + | |||
| + | ===הקדמה לקראת הוכחת משפט ההתמרה ההפוכה=== | ||
| + | |||
| + | *כעת נוכיח מספר טענות הדרושות לנו לצורך הוכחת משפט ההתמרה ההפוכה. | ||
| + | |||
| + | |||
| + | ====למת רימן-לבג==== | ||
| + | *ראינו גרסא של למת רימן-לבג עבור טורי פוריה, לפי מקדמי הפורייה שואפים לאפס. | ||
| + | *כעת ננסח ונוכיח גרסא עבור התמרות פורייה: | ||
| + | |||
| + | |||
| + | *תהי <math>f\in G</math>, אזי <math>\lim_{s\to\pm\infty}\mathcal{F}[f](s)=0</math> | ||
| + | *(כלומר, האמפליטודות שואפות לאפס כאשר התדר שואף לאינסוף) | ||
| + | |||
| + | |||
| + | *נוכיח את הלמה: | ||
| + | |||
| + | |||
| + | *צ"ל כי<math>\lim_{s\to\pm\infty}\frac{1}{2\pi}\int_{-\infty}^\infty f(x)e^{-isx}dx =0</math> | ||
| + | *נשים לב כי <math>e^{-isx}=\cos(sx)-i\sin(sx)</math>. | ||
| + | *לכן מספיק לנו להוכיח כי <math>\lim_{s\to\pm\infty}\frac{1}{2\pi}\int_{-\infty}^\infty f(x)\cos(sx)dx =0</math> (ההוכחה עבור סינוס דומה). | ||
| + | *כיוון ש<math>f\in G</math> האינטגרל <math>\int_{-\infty}^{\infty}|f(x)|dx</math> מתכנס. | ||
| + | *לכן קיים <math>M</math> עבורו <math>\int_{|x|>M}|f(x)|dx<\frac{\varepsilon}{2}</math>. | ||
| + | *לכן <math>|\int_{|x|>M}f(x)\cos(sx)dx|\leq \int_{|x|>M}|f(x)|dx < \frac{\varepsilon}{2}</math> | ||
| + | *לכן מספיק לנו להוכיח כי עבור <math>|s|</math> מספיק גדול מתקיים <math>|\int_{-M}^{M}f(x)\cos(sx)dx| < \frac{\varepsilon}{2}</math> | ||
| + | *(עבור <math>M=\pi</math> ו<math>s\in\mathbb{N}</math> כבר הוכחנו טענה זו בעזרת פרסבל, כעת נשתמש בשיטות אחרות.) | ||
| + | |||
| + | |||
| + | *נשים לב כי בכל קטע מתקיים: | ||
| + | **<math>\lim_{s\to\pm\infty}\int_{x_1}^{x_2}\cos(sx)dx = \lim_{s\to\pm\infty}\frac{\sin(sx_2)-\sin(sx_1)}{s}=0</math> | ||
| + | *כיוון ש<math>f</math> רציפה למקוטעין היא אינטגרבילית ב<math>[-M,M]</math>. | ||
| + | *לכן ניתן לבחור פונקצית מדרגות <math>h</math> עבורה מתקיים <math>\int_{-M}^M |f-h|dx < \frac{\varepsilon}{4}</math> (האינטגרל על פונקצית המדרגות הינו סכום דרבו תחתון מספיק קרוב). | ||
| + | *כמו כן מתקיים: | ||
| + | **<math>\int_{-M}^Mh\cos(sx)dx = \sum \int_{x_{i-1}}^{x_i}m_i\cos(sx)dx</math> | ||
| + | **כיוון שמדובר בסכום סופי של ביטויים ששואפים לאפס, הסכום גם שואף לאפס. | ||
| + | *סה"כ <math>\int_{-M}^{M}f(x)\cos(sx)dx = \int_{-M}^{M}(f(x)-h(x))\cos(sx)dx + \int_{-M}^{M}h(x)\cos(sx)dx</math> | ||
| + | **מתקיים כי <math>|\int_{-M}^{M}(f(x)-h(x))\cos(sx)dx|\leq \int_{-M}^{M}|f(x)-h(x)|dx < \frac{\varepsilon}{4}</math> | ||
| + | **עבור <math>|s|</math> מספיק גדול מתקיים כי <math>|\int_{-M}^{M}h(x)\cos(sx)dx|< \frac{\varepsilon}{4}</math> | ||
| + | |||
| + | |||
| + | *סה"כ קיבלנו כי עבור <math>|s|</math> מספיק גדול מתקיים <math>|\int_{-\infty}^{\infty}f(x)\cos(sx)sx|<\varepsilon</math> | ||
| + | |||
| + | |||
| + | |||
| + | ====טענת עזר==== | ||
| + | *תהי <math>f\in G</math> ותהי x נק' בה הנגזרות החד צדדיות קיימות, אזי: | ||
| + | :<math>\lim_{n\to\infty} \frac{1}{\pi}\int_0^{\infty} f(x+t)\frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{f(x^+)}{2}</math> | ||
| + | :<math>\lim_{n\to\infty} \frac{1}{\pi}\int_{-\infty}^{0} f(x+t)\frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{f(x^-)}{2}</math> | ||
| + | |||
| + | |||
| + | *נוכיח את הטענה הראשונה, הטענה השנייה דומה. | ||
| + | |||
| + | |||
| + | *נגדיר את הפונקציה <math>g(t)=\begin{cases}\frac{f(x+t)}{t}& x\in [\pi,\infty)\\ 0 & x\in (-\infty,\pi)\end{cases}</math> | ||
| + | *כיוון ש<math>f\in G</math> נובע שגם <math>g\in G</math> הרי <math>\left|\frac{f(x+t)}{t}\right|\leq |f(x+t)|</math> עבור <math>t>\pi</math>. | ||
| + | *לכן לפי למת רימן-לבג נובע כי <math>\lim_{s\to\infty}\int_{-\infty}^{\infty}g(t)\sin(st)dt = 0</math> | ||
| + | *בפרט מתקיים גבול הסדרה: | ||
| + | **<math>\lim_{n\to\infty} \int_{-\infty}^{\infty}g(t)\sin\left((n+\frac{1}{2})t\right)dt =0</math> | ||
| + | *אבל <math>\int_{-\infty}^{\infty}g(t)\sin\left((n+\frac{1}{2})t\right)dt = \int_\pi^\infty \frac{f(x+t)}{t}\sin\left((n+\frac{1}{2})t\right)dt</math> | ||
| + | |||
| + | |||
| + | *לכן נותר להוכיח כי <math>\lim_{n\to\infty}\frac{1}{\pi}\int_0^{\pi} f(x+t)\frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{f(x^+)}{2}</math> | ||
| + | *נגדיר את הפונקציה <math>h(t)=f(x+t)\frac{2\sin(\frac{t}{2})}{t}</math>. | ||
| + | **אם נתקן את אי הרציפות הסליקה של <math>\frac{2\sin(\frac{t}{2})}{t}</math> נקבל טור טיילור שגזיר אינסוף פעמים. | ||
| + | **לכן הפוקנציה <math>h</math> רציפה למקוטעין ובעלת נגזרות חד צדדיות קיימות. | ||
| + | *כעת נשים לב כי: | ||
| + | **<math>\frac{1}{\pi}\int_0^{\pi} f(x+t)\frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{1}{\pi}\int_0^{\pi} h(t)\frac{\sin\left((n+\frac{1}{2})t\right)}{2\sin(\frac{t}{2})}dt | ||
| + | = \frac{1}{\pi}\int_0^{\pi} h(t)D_n(t)dt</math> | ||
| + | **לפי ההוכחה של משפט דיריכלה להתכנסות טורי פורייה, הגבול של הביטוי הזה שווה ל<math>\frac{h(0^+)}{2} = \frac{f(x^+)}{2}</math>. | ||
| + | |||
| + | |||
| + | =====דוגמא===== | ||
| + | *טענה: | ||
| + | :<math>\int_0^\infty \frac{\sin(x)}{x}dx = \frac{\pi}{2}</math> | ||
| + | |||
| + | |||
| + | *הוכחה: | ||
| + | **ראשית, אנו יודעים כי האינטגרל מתכנס לפי מבחן דיריכלה לאינטגרלים לא אמיתיים. | ||
| + | **לכן מתקיים כי <math>\int_0^\infty \frac{\sin(x)}{x}dx =\lim_{n\to\infty} \int_0^{(n+\frac{1}{2})\pi}\frac{\sin(x)}{x}dx</math> | ||
| + | **נבצע הצבה <math>t=\frac{x}{n+\frac{1}{2}}</math> ונקבל כי: | ||
| + | ***<math>\int_0^{(n+\frac{1}{2})\pi}\frac{\sin(x)}{x}dx = \int_0^\pi \frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt</math> | ||
| + | **עבור <math>f(x)=1</math>, לפי הוכחת טענת העזר נקבל כי הגבול הוא <math>\frac{\pi}{2}</math> | ||
| + | |||
| + | ===הוכחת משפט ההתמרה ההפוכה=== | ||
| + | *<math>\int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\mathcal{F}[f](s)e^{isx}ds = \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\left[\frac{1}{2\pi}\int_{-\infty}^\infty f(y)e^{-isy}dy\right]e^{isx}ds=</math> | ||
| + | *<math>=\frac{1}{2\pi} \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\int_{-\infty}^\infty f(y)e^{is(x-y)}dyds</math> | ||
| + | *נחליף את סדר האינטגרציה (הצדקה בהמשך), ונקבל: | ||
| + | *<math>\frac{1}{2\pi}\int_{-\infty}^\infty\int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}f(y)e^{is(x-y)}dsdy =</math> | ||
| + | *<math>\frac{1}{2\pi}\int_{-\infty}^\infty f(y) \left[\frac{e^{is(x-y)}}{i(x-y)}\right]_{-(n+\frac{1}{2})}^{n+\frac{1}{2}} dy =</math> | ||
| + | *<math>\frac{1}{2\pi}\int_{-\infty}^\infty f(y) \frac{2\sin\left((n+\frac{1}{2})(x-y)\right)}{(x-y)} dy</math> | ||
| + | *נציב <math>t=y-x</math> ונקבל: | ||
| + | *<math>\frac{1}{\pi}\int_{-\infty}^\infty f(x+t) \frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{f(x^+)+f(x^-)}{2}</math> | ||
| + | כאשר המעבר האחרון הוא בזכות טענת העזר לעיל. | ||
| + | |||
| + | |||
| + | ====הצדקת החלפת סדר האינטגרציה==== | ||
| + | |||
| + | *נביט בסדרה <math>u_k(s)=\int_{-k}^k f(y)e^{is(x-y)}dy</math>, שמתכנסת כמובן ל<math>\int_{-\infty}^\infty f(y)e^{is(x-y)}dy</math> | ||
| + | *מתקיים כי <math>|\int_{-\infty}^\infty f(y)e^{is(x-y)}dy - u_k(s)| \leq \int_{|y|>k} |f(y)e^{is(x-y)}|dy = \int_{|y|>k} |f(y)|dy\to 0</math> | ||
| + | **(נתון כי <math>f\in G</math>) | ||
| + | *לכן הסדרה מתכנסת במ"ש ומותר לבצע אינטגרציה איבר איבר: | ||
| + | **<math>\int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\int_{-\infty}^\infty f(y)e^{is(x-y)}dyds = \lim_{k\to\infty} \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}} u_k(s)ds</math> | ||
| + | **לפי פוביני מותר לנו להחליף את סדר האינטגרציה ונקבל כי | ||
| + | **<math>\int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\int_{-\infty}^\infty f(y)e^{is(x-y)}dyds = \lim_{k\to\infty} \int_{-k}^k \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}f(y)e^{is(x-y)}dsdy = \int_{-\infty}^\infty \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}f(y)e^{is(x-y)}dsdy</math> | ||
| + | **שימו לב שהאינטגרל הלא אמיתי אכן מתכנס (כפי שהוכחנו לעיל) ולכן שווה לגבול. | ||
| + | |||
| + | ==הרצאה 9 - קונבולוציה, משוואת החום על מוט אינסופי== | ||
| + | |||
| + | *תהיינה <math>f,g:\mathbb{R}\to\mathbb{C}</math> פונקציות, נגדיר את ה'''קונבולוציה''' ביניהן להיות: | ||
| + | **<math>f*g(x) = \int_{-\infty}^\infty f(x-y)g(y)dy</math>. | ||
| + | |||
| + | |||
| + | *מוטיבציה לדוגמא: | ||
| + | **אם <math>f,g</math> הן פונקציות צפיפות של משתנים מקריים, מהי פונקציית הצפיפות של סכום המשתנים? | ||
| + | **הסיכוי שסכום המשתנים יהיה x, הוא סכום מכפלות הסיכויים שמשתנה אחד יהיה שווה y והשני יהיה שווה x-y. | ||
| + | |||
| + | |||
| + | *הקונבולוציה היא אבלית: | ||
| + | **<math>g*f = \int_{-\infty}^\infty g(x-y)f(y)dy = \{t=x-y,dt=-dy\} = \int_{-\infty}^\infty g(t)f(x-t)dt = f*g</math> | ||
| + | |||
| + | |||
| + | *שימו לב: בנושא זה נבצע החלפת סדר אינטגרציה, אך לא נצדיק החלפה זו כיוון שהיא דורשת העמקה רבה. | ||
| + | *ניתן להעמיק ע"י קריאה בספר Fourier Analysis של T.W.Korner | ||
| + | |||
| + | |||
| + | *משפט הקונבולוציה: | ||
| + | *תהיינה <math>f,g\in G</math> רציפות וחסומות אזי <math>\mathcal{F}[f*g] = 2\pi \cdot \mathcal{F}[f] \cdot \mathcal{F}[g]</math> | ||
| + | |||
| + | |||
| + | *הסבר המשפט (לא הוכחה מלאה, כיוון שאנו מחליפים סדר אינטגרציה ללא הצדקה): | ||
| + | :<math>\mathcal{F}[f*g] = \frac{1}{2\pi}\int_{-\infty}^\infty \left[\int_{-\infty}^\infty f(x-y)g(y)dy\right]e^{-isx}dx = </math> | ||
| + | :<math>= \frac{1}{2\pi}\int_{-\infty}^\infty \int_{-\infty}^\infty f(x-y)e^{-is(x-y)}g(y)e^{-isy}dydx =</math> | ||
| + | :<math>= \frac{1}{2\pi}\int_{-\infty}^\infty \int_{-\infty}^\infty f(x-y)e^{-is(x-y)}g(y)e^{-isy}dxdy =</math> | ||
| + | :<math>= \frac{1}{2\pi}\int_{-\infty}^\infty \left[\int_{-\infty}^\infty f(x-y)e^{-is(x-y)}dx\right] g(y)e^{-isy}dy =</math> | ||
| + | :<math>= \frac{1}{2\pi}\int_{-\infty}^\infty \left[\int_{-\infty}^\infty f(t)e^{-ist}dt\right] g(y)e^{-isy}dy =</math> | ||
| + | :<math>= 2\pi\left(\frac{1}{2\pi}\int_{-\infty}^\infty f(t)e^{-ist}dt\right) \cdot \left( \frac{1}{2\pi}\int_{-\infty}^\infty g(y)e^{-isy}dy\right) =2\pi \cdot \mathcal{F}[f] \cdot \mathcal{F}[g]</math> | ||
| + | |||
| + | |||
| + | ===משוואת החום על מוט אינסופי=== | ||
| + | |||
| + | *אם פונקצית החום על מוט אינסופי היא <math>u(x,t)</math>, היא מקיימת את המשוואה <math>u_t-ku_{xx}=0</math>. | ||
| + | *נניח גם כי תנאי ההתחלה הם <math>u(x,0)=f(x)</math> (זה החום בכל נקודה במוט בזמן 0). | ||
| + | |||
| + | |||
| + | *נבצע התמרת פורייה של הפתרון לפי המשתנה x: | ||
| + | :<math>U(s,t)=\frac{1}{2\pi}\int_{-\infty}^{\infty} u(x,t)e^{-isx}dx</math> | ||
| + | *נגזור לפי המשתנה t: | ||
| + | :<math>U_t(s,t) = \frac{1}{2\pi}\int_{-\infty}^{\infty} u_t(x,t)e^{-isx}dx</math> | ||
| + | *(נניח כי הפתרון מקיים את התנאים שמאפשרים להחליף את סדר הגזירה והאינטגרציה, לא נרחיב על כך בהמשך) | ||
| + | *כיוון ש<math>u_t-ku_{xx}=0</math> נקבל כי: | ||
| + | :<math>U_t(s,t) = \frac{k}{2\pi}\int_{-\infty}^{\infty} u_{xx}(x,t)e^{-isx}dx</math> | ||
| + | *נזכר בנוסחאת התמרת הנגזרת <math>\mathcal{F}[f']=is\mathcal{F}[f]</math> | ||
| + | *ולכן נקבל כי: | ||
| + | :<math>U_t(s,t) = -s^2 \frac{k}{2\pi}\int_{-\infty}^\infty u(x,t)e^{-isx}dx = -ks^2 U(s,t)</math> | ||
| + | *זו מד"ר פשוטה שפתרונה הוא: | ||
| + | :<math>U(s,t) = A(s)e^{-ks^2 t}</math> | ||
| + | |||
| + | |||
| + | *נציב את תנאי ההתחלה <math>t=0</math> ונקבל כי | ||
| + | :<math>A(s) = U(s,0) = \frac{1}{2\pi}\int_{-\infty}^{\infty} u(x,0)e^{-isx}dx = \frac{1}{2\pi}\int_{-\infty}^{\infty} f(x)e^{-isx}dx = \mathcal{F}[f]</math> | ||
| + | *לכן בעצם מתקיים כי <math>U(s,t)= F(s)e^{-ks^2 t}</math> | ||
| + | *קיבלנו שההתמרה של הפתרון היא מכפלה של שתי התמרות, ולכן הפתרון הוא הקונבולוציה של שתי הפונקציות המקוריות. | ||
| + | |||
| + | |||
| + | *נחפש את ההתמרה ההפוכה של <math>e^{-ks^2 t}</math> | ||
| + | *נזכור כי <math>\mathcal{F}[e^{-x^2}] = \frac{1}{2\sqrt{\pi}} e^{-\frac{s^2}{4}}</math> | ||
| + | :<math>\mathcal{F}^{-1}[e^{-ks^2 t}]=\int_{-\infty}^\infty e^{-ks^2 t}e^{isx}ds = \{s=\frac{u}{2\sqrt{kt}}\}=</math> | ||
| + | :<math>=\frac{1}{2\sqrt{kt}}\int_{-\infty}^\infty e^{-\frac{u^2}{4}}e^{iu(\frac{x}{2\sqrt{kt}})}du = \frac{2\sqrt{\pi}}{2\sqrt{kt}} \mathcal{F}^{-1}[\frac{1}{2\sqrt{\pi}}e^{-\frac{u^2}{4}}](\frac{x}{2\sqrt{kt}}) = \frac{\sqrt{\pi}}{\sqrt{kt}}e^{-\frac{x^2}{4kt}}</math> | ||
| + | *נסמן פונקציה זו ב<math>p(x,t)=\frac{\sqrt{\pi}}{\sqrt{kt}}e^{-\frac{x^2}{4kt}}</math> | ||
| + | |||
| + | |||
| + | *לכן עבור פתרון מד"ח החום u מתקיים כי: | ||
| + | :<math>\mathcal{F}[u] = \mathcal{F}[f]\cdot \mathcal{F}[p]</math> | ||
| + | *ולכן לפי משפט הקונבולוציה מתקיים כי | ||
| + | :<math> u(x,t) = \frac{1}{2\pi} f*p(x,t)</math> | ||
| + | *שימו לב שהקונבולוציה היא לפי המשתנה x. | ||
| + | *לכן | ||
| + | :<math>u(x,t) = \frac{1}{2\pi}\int_{-\infty}^\infty f(y)p(x-y,t)dy = \frac{1}{2\sqrt{\pi kt}}\int_{-\infty}^\infty f(y)e^{-\frac{(x-y)^2}{4kt}}dy</math> | ||
| + | |||
| + | |||
| + | *שימו לב שבפתרון הסופי מופיעה פונקצית תנאי ההתחלה, ואין צורך לחשב את ההתמרה שלה. | ||
| + | |||
| + | ==הרצאה 10 - משפט הדגימה של שנון== | ||
| + | ===משפט הדגימה של שנון=== | ||
| + | *תהי פונקציה f. ברור שבהנתן הערכים של f על השלמים <math>f(0),f(\pm 1),f(\pm 2),...</math> לא ניתן להסיק כלום על ערכיה האחרים (אפילו אם היא רציפה וגזירה). | ||
| + | *בפרט אם נדגום באופן דומה את הפונקציה <math>sin(x)</math> בנקודות <math>2\pi n</math> אנחנו עשויים לחשוד שהיא קבועה לחלוטין. | ||
| + | *מה יקרה אם נדגום גל בקצב מהיר יותר מהתדר שלו? | ||
| + | *במילים פשוטות, משפט הדגימה של שנון אומר שבהנתן פונקציה שהתדרים שלה חסומים, אם נדגום אותה בקצב מהיר פי 2 מהתדר המקסימלי שלה, נוכל לשחזר אותה לחלוטין. | ||
| + | *כעת ננסח את המשפט במדויק, יחד עם ניסוח התנאים הנחוצים על הפונקציות. | ||
| + | |||
| + | |||
| + | *עד כה דיברנו על תדר כמדד לקצב בו הפונקציה חוזרת על עצמה, כעת נגדיר אותו במדויק: | ||
| + | *בהנתן פונקציה עם מחזור <math>t</math> נגדיר את התדר של המחזור להיות <math>\frac{1}{t}</math>. | ||
| + | *דוגמאות: | ||
| + | **התדר של <math>\sin(x)</math> הוא <math>\frac{1}{2\pi}</math> | ||
| + | **התדר של <math>\sin(\pi x)</math> הוא <math>\frac{1}{2}</math> | ||
| + | **באופן כללי, התדר של <math>sin(\pi t x)</math> הוא <math>\frac{t}{2}</math> כיוון ש <math>\sin(\pi t(x+\frac{2}{t})) = \sin(\pi t x)</math> | ||
| + | **התדר של <math>e^{isx}</math> הוא <math>\frac{|s|}{2\pi}</math> כיוון ש <math>e^{is(x+\frac{2\pi}{|s|})} = e^{isx\pm i2\pi} =e^{isx}</math> | ||
| + | |||
| + | |||
| + | *משפט הדגימה של שנון: | ||
| + | *תהי <math>f\in G</math> רציפה ובעלת נגזרת חד צדדיות הקיימות בכל נקודה, שתדריה חסומים על ידי <math>t</math>, אזי בהנתן דגימה שלה בתדר <math>2t</math> ניתן לשחזר אותה בכל הממשיים (כלומר היא נקבעת באופן יחיד על ידי הדגימות). | ||
| + | *שימו לב: הכוונה בכך שתדריה של הפונקציה חסומים, היא למעשה ש<math>\mathcal{F}[f](s)=0</math> לכל <math>\frac{|s|}{2\pi}>t</math>. | ||
| + | |||
| + | |||
| + | ====הוכחת משפט הדגימה==== | ||
| + | *כיוון שהתמרת הפורייה מתאפסת מחוץ לקטע <math>[-2\pi t,2\pi t]</math>, ניתן לקבוע כי | ||
| + | :<math>\int_{-\infty}^\infty \mathcal{F}[f](s)e^{isx}ds = \int_{-2\pi t}^{2\pi t}\mathcal{F}[f](s)e^{isx}ds</math> | ||
| + | *ובפרט האינטגרל מתכנס. | ||
| + | *לפי משפט ההתמרה ההפוכה, נובע כי <math>f(x)= \int_{-2\pi t}^{2\pi t}\mathcal{F}[f](s)e^{isx}ds</math> | ||
| + | |||
| + | |||
| + | *כעת, נתונה לנו סדרת הדגימות בתדר <math>2t</math>: | ||
| + | :<math>c_n = f\left(\frac{n}{2t}\right), n\in\mathbb{Z}</math> | ||
| + | *נציב אותן בנוסחא שמצאנו לעיל: | ||
| + | :<math>c_n = \int_{-2\pi t}^{2\pi t}\mathcal{F}[f](s)e^{is\left(\frac{n}{2t}\right)}ds</math> | ||
| + | *נבצע הצבה <math>\frac{s}{2t}=-x</math> ונקבל: | ||
| + | :<math>c_n = \int_{-\pi}^\pi \mathcal{F}[f](-2tx)e^{-inx}dx</math> | ||
| + | *אבל אלה בדיוק מקדמי פוריה (פרט לקבוע <math>\frac{1}{2\pi}</math>) של הפונקציה <math>\mathcal{F}[f](-2tx)</math>. | ||
| + | *כיוון שההתמרה חסומה בתדר, עבור <math>|x|\geq \pi</math> מתקיים כי <math>\mathcal{F}[f](-2tx)=0</math> (זכרו כי ההתמרה רציפה, ולכן מתאפסת גם בקצוות). | ||
| + | *לכן <math>\mathcal{F}[f](-2tx)</math> נקבעת על ידי ערכיה בקטע <math>(-\pi,\pi)</math>, והם נקבעים באופן יחיד על ידי מקדמי הפורייה (מסקנה מפרסבל). | ||
| + | *לבסוף, כפי שראינו לעיל, הפונקציה f נקבעת באופן יחיד על ידי ההתמרה (בזכות משפט ההתמרה ההפוכה). | ||
| + | |||
| + | |||
| + | ====הערות==== | ||
| + | *שימו לב שלא ניתן באופן פרקטי לדגום אות אנלוגי באינסוף נקודות. | ||
| + | *מה יקרה אם נדגום במספר סופי של נקודות ונניח כי הפונקציה ממשיכה באופן מחזורי? | ||
| + | *נקבל פונקציה שאינה שייכת ל<math>G</math>, כיוון שהאינטגרל שלה לא יכול להתכנס בכל הממשיים. | ||
| + | *בהמשך, נראה אנלוגיה למשפט הדגימה של שנון בהתמרת פורייה הבדידה. | ||
| + | |||
| + | |||
| + | ==הרצאה 11 - התמרת פורייה הבדידה== | ||
| + | |||
| + | ===DFT - Discrete Fourier transform=== | ||
| + | |||
| + | *תהי סדרת נקודות <math>a_0,...,a_{N-1} \in \mathbb{C}</math>, התמרת הפורייה הבדידה שלה היא סדרת הנקודות <math>A_0,...,A_{N-1}\in\mathbb{C}</math> המוגדרת ע"י: | ||
| + | :<math>A_n = \sum_{k=0}^{N-1} a_k e^{-2\pi i n\frac{k}{N}} </math> | ||
| + | |||
| + | |||
| + | *שימו לב שכמות הפעולות הנדרשות לחישוב ההתמרה באופן ישיר היא סדר גודל של <math>N^2</math>. | ||
| + | *התמרת פורייה המהירה (FFT) מבצעת את אותו חישוב בכמות פעולות בסדר גודל של <math>N\log(N)</math>. | ||
| + | |||
| + | |||
| + | ====משמעות ההתמרה==== | ||
| + | |||
| + | *תהי פונקציה f. נדגום ממנה <math>N</math> נקודות בתדר <math>t</math>, כלומר נתון לנו: | ||
| + | :<math>f(0),f(\frac{1}{t}),f(\frac{2}{t}),...,f(\frac{N-1}{t})</math> | ||
| + | *נסמן נקודות אלה ב<math>a_k=f(\frac{k}{t})</math> | ||
| + | |||
| + | *אנו רוצים לפרק אותה לסכום של גלים: | ||
| + | :<math>f(x)=B_0e^{2\pi i \cdot 0\cdot\frac{t}{N}x}+ B_1e^{2\pi i \cdot 1\cdot\frac{t}{N}x}+B_2e^{2\pi i \cdot 2\cdot\frac{t}{N}x}+...+B_{N-1}e^{2\pi i \cdot (N-1)\cdot\frac{t}{N}x}</math> | ||
| + | *כיוון שהתדר של <math>e^{isx}</math> הוא <math>\frac{|s|}{2\pi}</math> נובע כי הגלים הללו הם בתדרים <math>0,\frac{t}{N},\frac{2t}{N},...,\frac{(N-1)t}{N}</math> | ||
| + | *שימו לב - ככל שנדגום יותר נקודות נקבל יותר מגוון של תדרים. מצד שני, נביט בחלון זמן יותר ארוך ונפספס שינויי תדרים מהירים יותר. | ||
| + | |||
| + | |||
| + | *נוכיח שפירוק זה תמיד אפשרי כך שיהיה שיוויון בכל נקודות הדגימה, ונקשר בין סדרת המקדמים להתמרת הפורייה של נקודות הדגימה. | ||
| + | |||
| + | |||
| + | *נביט בפונקצית הגל <math>u_n(x)=e^{2\pi i n\frac{t}{N}x}</math>. | ||
| + | *נציב בה את נקודות הדגימה ונקבל את הוקטור המרוכב: | ||
| + | :<math>v_n= \left(u_n(0),u_n(\frac{1}{t}),...,u_n(\frac{N-1}{t})\right) = \left( 1,e^{2\pi i n \frac{1}{N}},e^{2\pi i n \frac{2}{N}},...,e^{2\pi i n \frac{N-1}{N}} \right)</math> | ||
| + | *נציב בפונקציה הנתונה f את נקודות הדגימה ונקבל את הוקטור המרוכב: | ||
| + | :<math>v=\left(f(0),f(\frac{1}{t}),f(\frac{2}{t}),...,f(\frac{N-1}{t})\right) = (a_0,...,a_{N-1})</math> | ||
| + | *לכן אנו מעוניינים בפתרון למשוואה: | ||
| + | :<math>v=B_0v_0+...+B_{N-1}v_{N-1}</math> | ||
| + | *זה בדיוק אומר שהפירוק של הפונקציה לגלים מתקיים בכל נקודות הדגימה: | ||
| + | :<math>f(\frac{k}{t}) = B_0u_0(\frac{k}{t})+...+B_{N-1}u_{N-1}(\frac{k}{t})</math> | ||
| + | |||
| + | |||
| + | *נבחן את הקבוצה <math>\{v_0,...,v_{N-1}\}</math>. | ||
| + | :<math>\langle v_n,v_n\rangle = v_n^t \overline{v_n} = \sum_{k=0}^{N-1} e^{2\pi i n \frac{k}{N}}\cdot e^{-2\pi i n \frac{k}{N}}= 1+1+...+1= N</math> | ||
| + | *עבור <math>n\neq m</math>: | ||
| + | :<math>\langle v_n,v_m\rangle = \sum_{k=0}^{N-1} e^{2\pi i n \frac{k}{N}}\cdot e^{-2\pi i m \frac{k}{N}} = \sum_{k=0}^{N-1} e^{2\pi i (n-m) \frac{k}{N}}</math> | ||
| + | *אבל זה בדיוק סכום סדרה הנדסית <math>1+q+...+q^{N-1}</math> עבור <math>q=e^{2\pi i (n-m)\frac{1}{N}}</math> | ||
| + | *שימו לב ש<math>\frac{|n-m|}{N}<1</math> ולכן <math>q\neq 1</math>. | ||
| + | *כמו כן, שימו לב ש<math>q^N = e^{2\pi i (n-m)}=1</math> | ||
| + | *לכן לפי הנוסחא לסכום סדרה הנדסית נקבל כי: | ||
| + | :<math>\langle v_n,v_m\rangle = \frac{1-q^N}{1-q}=0</math> | ||
| + | *כלומר גילינו כי <math>\{v_0,...,v_{N-1}\}</math> קבוצה אורתוגונלית (לא אורתונורמלית) ומהווה בסיס. | ||
| + | *לכן ניתן בקלות לחשב את המקדמים <math>B_n = \frac{\langle v,v_n\rangle}{N}</math> | ||
| + | |||
| + | |||
| + | *לבסוף, נשים לב כי: | ||
| + | :<math>\langle v,v_n\rangle = \sum_{k=0}^{N-1} a_k e^{-2\pi i n \frac{k}{N}} = A_n</math> | ||
| + | *כלומר <math>B_n = \frac{A_n}{N}</math> | ||
| + | |||
| + | ====התמרת פורייה הבדידה ההפוכה==== | ||
| + | *מכאן גם ניתן להסיק ישירות את התמרת פורייה ההפוכה, שמחזירה את סדרת המקדמים <math>A_n</math> לסדרת הדגימות <math>a_n</math>. | ||
| + | :<math>v=\frac{1}{N}(A_0v_0+...+A_{N-1}v_{N-1})</math> | ||
| + | *ולכן: | ||
| + | :<math>a_n = \frac{1}{N}\sum_{k=0}^{N-1} A_k e^{2\pi i k \frac{n}{N}}</math> | ||
| + | |||
| + | |||
| + | ====מסקנות לגבי גלים ממשיים==== | ||
| + | *פירקנו את הפונקציה לסכום של גלים מרוכבים בנקודות הדגימה, האם ניתן להשתמש בהתמרה על מנת לקבל פירוק לגלים ממשיים? | ||
| + | |||
| + | |||
| + | *ראשית, נשים לב לתופעה הבאה: | ||
| + | :<math>v_{N-n} = (1,e^{2\pi i (N-n) \frac{1}{N}},...,e^{2\pi i (N-n) \frac{N-1}{N}}) = (1,e^{2\pi i (N-n) \frac{1}{N} - 2\pi i },...,e^{2\pi i (N-n) \frac{N-1}{N} - 2\pi i (N-1)})</math> | ||
| + | *(השיוויון נכון בזכות המחזוריות) | ||
| + | *ולכן נקבל: | ||
| + | :<math>v_{N-n} = (1, e^{2\pi i (\frac{(N-n)}{N} - 1)},...,e^{2\pi i (N-1)(\frac{(N-n)}{N} - 1)}) = v_{-n}</math> | ||
| + | |||
| + | |||
| + | *כלומר פירוק הפונקציה לגלים <math>u_0,u_1,...,u_{N-1}</math> נותן את אותם המקדמים כמו פירוק הפונקציה לגלים <math>u_0,u_1,u_{-1},...</math>. | ||
| + | *כאשר המקדם של <math>u_{-n}</math> שווה למקדם של <math>u_{N-n}</math>. | ||
| + | *שימו לב שזה לא פירוק של הפונקציה לסכום הגלים בכל הממשיים, אלא רק בנקודות הדגימה. | ||
| + | |||
| + | |||
| + | *לדוגמא: | ||
| + | *נניח שיש לנו 5 דגימות של f. | ||
| + | *אם נפרק את f לגלים <math>u_0,u_1,...,u_5</math> נקבל <math>v=B_0v_0+...+B_4v_4</math> | ||
| + | *אם נפרק את f לגלים <math>u_{-2},u_{-1},u_0,u_1,u_2</math> נקבל <math>v=B_3v_{-2},B_4v_{-1}+B_0v_0+B_1v_1+B_2v_2</math> | ||
| + | *במצב זה, אם דגמנו בתדר <math>t</math> נקבל את התדרים <math>0,\frac{t}{5},\frac{2t}{5}</math> שזה מתאים למשפט הדגימה של שנון (טווח התדרים של הפונקציה הוא עד חצי מתדר הדגימה). | ||
| + | |||
| + | |||
| + | *עבור n ספציפי מתקיים כי: | ||
| + | :<math>B_ne^{2\pi i n \frac{t}{N}x} + B_{N-n}e^{-2\pi i n \frac{t}{N}x} = (B_n+B_{N-n}) \cos (2\pi n \frac{t}{N}x) + i(B_n-B_{N-n})sin(2\pi n \frac{t}{N}x)</math> | ||
| + | *מהצבה ישירה של הנוסחאות שמצאנו ניתן לראות שאם f ממשית אזי <math>B_n+B_{N-n}</math> וגם <math>i(B_n-B_{N-n})</math> הם ממשיים. | ||
| + | *כלומר הצלחנו לפרק את f לסכום של גלים ממשיים עם מקדמים ממשיים. | ||
| + | |||
| + | |||
| + | *הערה: אם N זוגי, אז הגל <math>u_{\frac{N}{2}}</math> נותר בודד. | ||
| + | *לדוגמא עבור <math>N=4</math> נקבל במקום הגלים <math>u_0,u_1,u_2,u_3</math> את <math>u_{-1},u_0,u_1,u_2</math> | ||
| + | *נשים לב כי במקרה זה <math>v_{\frac{N}{2}}</math> הוא וקטור ממשי (ולכן גם המקדם שלו ממשי) כיוון שהsin מתאפס בכל נקודות הדגימה. | ||
גרסה אחרונה מ־08:15, 16 במאי 2022
תוכן עניינים
- 1 מבחנים לדוגמא
- 2 תקציר ההרצאות
- 2.1 הרצאה 1 - הקדמה ומקדמי פוריה
- 2.2 הרצאה 2 - למת רימן לבג, גרעין דיריכלה
- 2.3 הרצאה 3 התכנסות נקודתית של טורי פוריה
- 2.4 הרצאה 4 - התכנסות במ"ש ושיוויון פרסבל
- 2.5 הרצאה 5 - תופעת גיבס, טורי הסינוסים והקוסינוסים
- 2.6 הרצאה 6 - משוואת החום על טבעת, התמרת פורייה
- 2.7 הרצאה 7 - תכונות של התמרות פורייה
- 2.8 הרצאה 8 - התמרה הפוכה
- 2.9 הרצאה 9 - קונבולוציה, משוואת החום על מוט אינסופי
- 2.10 הרצאה 10 - משפט הדגימה של שנון
- 2.11 הרצאה 11 - התמרת פורייה הבדידה
מבחנים לדוגמא
תקציר ההרצאות
- ההרצאות מבוססות בחלקן על הספר המצויין 'טורי פוריה' של זעפרני ופינקוס.
עוד ספרים מתמטיים בסגנון ניתן למצוא באתר של סמי זערפני.
הרצאה 1 - הקדמה ומקדמי פוריה
הקדמה - גלים
- מבלי להגדיר גל במפורש, גל הוא תופעה מחזורית.
- לגל שהוא פונקציה במשתנה אחד של ציר הזמן יש שלוש תכונות:
- תדר או אורך גל (אחד חלקי המחזור או המחזור)
- אמפליטודה (מרחק בין המקסימום למינימום)
- פאזה (מהי נק' ההתחלה של המחזור).
- אנחנו נתרכז כמעט באופן בלעדי בפונקציות הטריגונומטריות סינוס וקוסינוס, ונקרא להם גלים טריגונומטריים.
- מדוע דווקא סינוס וקוסינוס?
- למדנו במד"ר על המשוואה
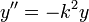 המתארת תנועה על מסה המחוברת לקפיץ
המתארת תנועה על מסה המחוברת לקפיץ - זו למעשה תנועה כללית של גל - ככל שהוא מתרחק, גדל הכוח שמושך אותו למרכז. מיתר גיטרה הוא דוגמא טובה נוספת.
- הפתרון הכללי למד"ר הוא
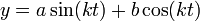 .
. - הקבוע
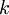 קובע את התדר של כל גל.
קובע את התדר של כל גל. - הקבועים
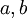 קובעים את האמפליטודה של כל גל.
קובעים את האמפליטודה של כל גל. - מה לגבי הפאזה?
- בפונקציה
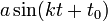 , הקבוע
, הקבוע 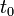 קובע את הפאזה.
קובע את הפאזה. - ניתן להציג כל גל כזה באמצעות סינוס וקוסינוס ללא פאזה:
- בפונקציה
- האם גם ההפך נכון? כלומר האם כל צירוף לינארי
 ניתן להציג כגל יחיד?
ניתן להציג כגל יחיד? - תשובה: כן.
- הוכחה:
- נסמן
- כלומר
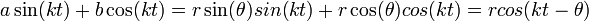
- נסמן
- שימו לב:
- סכמנו שני גלים מאותו תדר עם פאזה אפס, וקיבלנו גל חדש.
- הגל החדש הוא מאותו תדר כמו שני הגלים.
- לגל החדש יש פאזה שאינה אפס.
- האפליטודה של הגל החדש היא
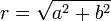 .
.
- האם כל פונקציה היא סכום של גלים?
- בהנתן פונקציה שהיא סכום של גלים, כיצד נמצא מיהם הגלים המרכיבים אותה?
- האם יש דרך יחידה להרכיב פונקציה מגלים? (למעשה כבר ראינו שלא באופן כללי - הרי הצלחנו להציג גל אחד כסכום של שני גלים אחרים).
- למה בכלל מעניין אותנו לפרק פונקציה לגלים?
- במהלך ההרצאות נענה (לפחות חלקית) על השאלות הללו.
טורי פורייה ומקדמי פוריה
- טור פורייה הוא טור מהצורה
![f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty \left[a_n\cos(nx)+b_n\sin(nx)\right]](/images/math/6/6/c/66c1bbf99995adc693d0394e5f637359.png)
- אם פונקציה שווה לטור פורייה שלה, מהם המקדמים
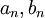 ?
?
חישובים להקדמה
- ראשית נזכור את הנוסחאות הטריגונומטריות:
- כעת, לכל
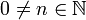 נקבל:
נקבל:
- עבור
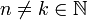 נקבל:
נקבל:
![\int_{-\pi}^{\pi}\sin(nx)\sin(kx)dx = \frac{1}{2}\int_{-\pi}^{\pi}(\cos((n-k)x)-\cos((n+k)x))dx = \frac{1}{2}\left[\frac{\sin((n-k)x)}{n-k}-\frac{\sin((n+k)x)}{n+k}\right]_{-\pi}^{\pi}=0](/images/math/8/f/b/8fbca5cb5a1f31c0bdbb8c0c68cc16b9.png)
- שימו לב כי השתמשנו כאן בעובדה ש
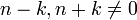 .
.
- באופן דומה, לכל
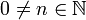 נקבל:
נקבל:
- עבור
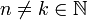 נקבל:
נקבל:
![\int_{-\pi}^{\pi}\cos(nx)\cos(kx)dx = \frac{1}{2}\int_{-\pi}^{\pi}(\cos((n+k)x)+\cos((n-k)x))dx = \frac{1}{2}\left[\frac{\sin((n+k)x)}{n+k}+\frac{\sin((n-k)x)}{n-k}\right]_{-\pi}^{\pi}=0](/images/math/7/d/6/7d6a0fcc6eaaef72edacd68b4278e786.png)
- שימו לב כי השתמשנו כאן בעובדה ש
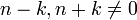 .
.
- עבור
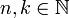 נקבל:
נקבל:
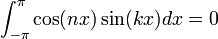 כיוון שמדובר באינטגרל בקטע סימטרי על פונקציה אי זוגית.
כיוון שמדובר באינטגרל בקטע סימטרי על פונקציה אי זוגית.
- ולבסוף, עבור
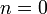 נקבל
נקבל
- שימו לב שכאשר מציבים 0 בsin מקבלים אפס, ולכן אין צורך בבדיקה הזו.
- כמו כן קל לחשב
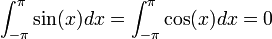
- הערה חשובה:
- למעשה כלל החישובים שעשינו לעיל מוכיחים שהקבוצה
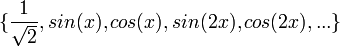 מהווה קבוצה אורתונורמלית לפי המכפלה הפנימית
מהווה קבוצה אורתונורמלית לפי המכפלה הפנימית 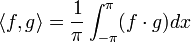
- למעשה כלל החישובים שעשינו לעיל מוכיחים שהקבוצה
מקדמי הטור
- כעת תהי פונקציה ששווה לטור פורייה, ועוד נניח שהטור מתכנס במ"ש.
![\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(kx)dx = \frac{1}{\pi}\int_{-\pi}^{\pi}\left(\frac{a_0}{2}+\sum_{n=1}^\infty \left[a_n\cos(nx)+b_n\sin(nx)\right]\right)\cos(kx)dx=](/images/math/a/1/8/a18fda320cac6333a54d8dc7285a69f2.png)
![=\frac{1}{\pi}\int_{-\pi}^{\pi}\left(\frac{a_0}{2}\cos(kx)+\sum_{n=1}^\infty \left[a_n\cos(nx)\cos(kx)+b_n\sin(nx)\cos(kx)\right]\right)dx=](/images/math/6/a/9/6a94fbbbdf98411fd913d8c54bf08f53.png)
- כיוון שהטור מתכנס במ"ש, מותר לנו לעשות אינטגרציה איבר איבר
![=\frac{1}{\pi}\int_{-\pi}^{\pi}\frac{a_0}{2}\cos(kx)dx + \sum_{n=1}^\infty \left[\frac{1}{\pi}\int_{-\pi}^{\pi}\left(a_n\cos(nx)\cos(kx)+b_n\sin(nx)\cos(kx)\right)dx\right]](/images/math/0/e/8/0e840fbc166461424acf8a0a238acdc2.png)
- לפי חישובי האינטגרלים לעיל, כמעט הכל מתאפס וסה"כ נקבל:
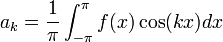
- שימו לב שחישוב זה נכון בפרט עבור
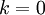 .
. - באופן דומה נקבל כי
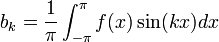
- הוכחנו שאם פונקציה שווה לטור פורייה, והטור מתכנס במ"ש, אזי הוא יחיד והמקדמים שלו נקבעים על ידי הנוסחאות לעיל.
- השאלה היא אילו פונקציות שוות לטור פורייה.
- באופן מיידי, ברור שטור פורייה הוא פונקציה עם מחזור
 .
. - לכן בדר"כ אנו שואלים האם ההמשך המחזורי של הפונקציה שווה לטור פורייה:
- תהי פונקציה
 , נגדיר את ההמשך המחזורי שלה
, נגדיר את ההמשך המחזורי שלה 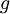 על ידי:
על ידי: - לכל
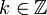 ולכל
ולכל 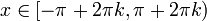 נגדיר
נגדיר 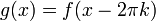 .
. - ברור ש
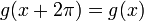 , כלומר קיבלנו פונקציה מחזורית.
, כלומר קיבלנו פונקציה מחזורית. - ניתן גם לרשום בנוסחא מקוצרת
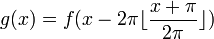
- תהי פונקציה
- לדוגמא, ההמשך המחזורי של
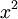 :
:
דוגמא
- נחשב את מקדמי הפורייה של ההמשך המחזורי של
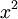
- שימו לב, מקדמי הפורייה של פונקציה וההמשך המחזורי שלה זהים, כיוון שערך הפונקציה בנקודה אחת לא משפיע על האינטגרל.
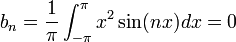 .
.
- שימו לב: מקדמי הפורייה של הסינוסים תמיד יתאפסו עבור פונקציה זוגית, ומקדמי הפורייה של הקוסינוסים תמיד יתאפסו עבור פונקציה אי זוגית.
- שימו לב כי לכל
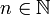 מתקיים כי
מתקיים כי 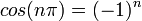
- סה"כ אם ההמשך המחזורי של
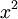 שווה לטור פורייה שמתכנס במ"ש, אזי טור זה הוא:
שווה לטור פורייה שמתכנס במ"ש, אזי טור זה הוא:
- נניח (ונוכיח בהמשך) שטור זה אכן שווה לפונקציה ונציב
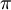 .
. 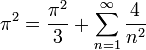
- ונקבל את הסכום המפורסם
הרצאה 2 - למת רימן לבג, גרעין דיריכלה
מרחבי מכפלה פנימית שאינם ממימד סופי והיטלים
- פונקציה נקראת רציפה למקוטעין בקטע סופי אם:
- 1. היא רציפה פרט אולי למספר סופי של נקודות.
- 2. הגבולות החד צדדיים הרלוונטיים בכל נקודה הם סופיים.
- למעשה נקודות אי הרציפות היחידות של פונקציה רציפה למקוטעין הן ממין ראשון (קפיצתיות).
- פונקציה נקראת רציפה למקוטעין בקטע כללי, אם ניתן לחלק אותו לקטעים סופיים בהן הפונקציה רציפה למקוטעין.
- E הוא המרחב הוקטורי של כל הפונקציות הרציפות למקוטעין
![f:[-\pi,\pi]\to\mathbb{C}](/images/math/2/c/b/2cb36383da87b746f0502644a80815b8.png) מעל השדה
מעל השדה 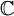 , המקיימות בנוסף שבכל נקודה ערך הפונקציה שווה לממוצע בין הגבולות החד צדדיים שלה, ובקצוות ערך הנקודה שווה לגבול החד צדדי המוגדר.
, המקיימות בנוסף שבכל נקודה ערך הפונקציה שווה לממוצע בין הגבולות החד צדדיים שלה, ובקצוות ערך הנקודה שווה לגבול החד צדדי המוגדר.
- לא קשה להוכיח שאכן מדובר במרחב וקטורי. בעיקר יש לשים לב לכך שסכום פונקציות בקבוצה נשאר בקבוצה.
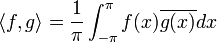 היא מכפלה פנימית מעל E.
היא מכפלה פנימית מעל E.
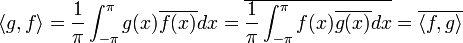
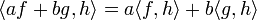
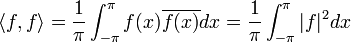
- בכל קטע רציפות האינטגרל על פונקציה חיובית הוא אפס אם ורק אם היא אפס.
- כיוון שהפונקציה בכל נקודה שווה לאחד הגבולות החד צדדיים או לממוצע בניהם, נובע שאם האינטגרל לעיל מתאפס הפונקציה חייבת להתאפס לחלוטין.
- נביט בנורמה המושרית
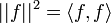
- כעת נוכיח מספר תכונות של היטלים במרחבי מכפלה פנימית.
- יש לנקוט בזהירות מיוחדת בנושא זה, כיוון שאנו עוסקים במרחבים שאינם נוצרים סופית (אין להם בסיס סופי או מימד).
- ייתכן שהוכחתם חלק מהמשפטים הבאים רק עבור מרחבים נוצרים סופית.
- תהי קבוצה אורתונורמלית סופית
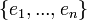 , ונקרא למרחב שהיא פורשת W.
, ונקרא למרחב שהיא פורשת W. - לכל וקטור
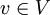 נגדיר את ההיטל של
נגדיר את ההיטל של 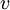 על W על ידי
על W על ידי 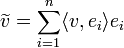
- נוכיח מספר תכונות לגבי ההיטל הזה:
- מתקיים כי
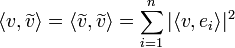
- הוכחה:
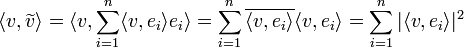
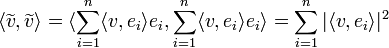
- המעבר האחרון נכון כיוון ש
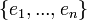 אורתונורמלית.
אורתונורמלית.
- מתקיים כי
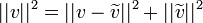
- הוכחה:
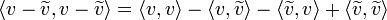
- נזכור כי
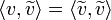 .
. - לכן קיבלנו כי
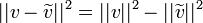
- מסקנה מיידית:
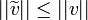
אי שיוויון בסל
- כעת תהי קבוצה אורתונורמלית אינסופית
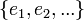 .
. - לכל
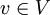 מתקיים כי
מתקיים כי 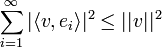
- הוכחה:
- ראינו שלכל n מתקיים כי
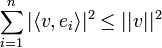 .
. - כלומר סדרת הסכומים החלקיים של הטור החיובי חסומה על ידי
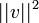 ולכן הטור מתכנס למספר שקטן או שווה לו.
ולכן הטור מתכנס למספר שקטן או שווה לו.
- בפרט נובע כי
למת רימן לבג
- ראינו כי
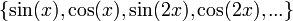 היא קבוצה אורתונורמלית ב
היא קבוצה אורתונורמלית ב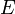 (כרגע אנו לא צריכים את הפונקציה הקבועה).
(כרגע אנו לא צריכים את הפונקציה הקבועה). - כמו כן לכל פונקציה f הגדרנו מקדמי פורייה ע"י:
- לכל
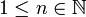 הגדרנו
הגדרנו 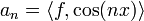 , ו
, ו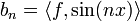
- נובע מאי שיוויון בסל כי המקדמים שואפים לאפס.
- כלומר:
- למת רימן-לבג: תהי
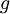 רציפה למקוטעין בקטע
רציפה למקוטעין בקטע ![[0,\pi]](/images/math/e/1/8/e1868564b62b4e2f1c063321df289469.png) , אזי:
, אזי:
- הוכחה:
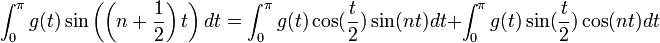
- נגדיר את שתי הפונקציות
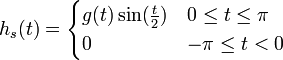 ו
ו 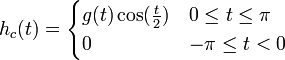
- קל לראות כי שתי הפונקציות רציפות למקוטעין. לכן פרט לשינוי במספר סופי של נקודות שלא משפיע על האינטגרל, ניתן להניח כי
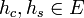 .
. - ביחד נקבל כי
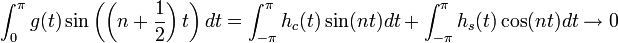
גרעין דיריכלה
- גרעין דיריכלה הוא הפונקציה
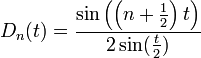
- טענה:
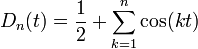 בכל נקודה
בכל נקודה 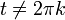
- הוכחה:
- נכפל ב
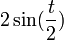 ונקבל בצד שמאל:
ונקבל בצד שמאל: 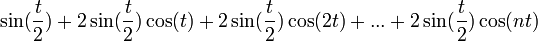
- נבחין בזהות הטריגונומטרית
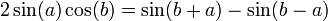
- ובפרט
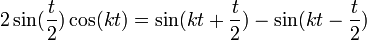
- ביחד נקבל
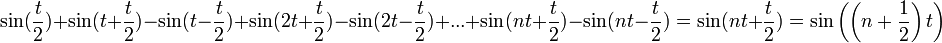
- נשים לב כי הפונקציה
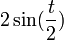 מתאפסת בנקודות
מתאפסת בנקודות 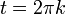 , בנקודות אלו לגרעין דיריכלה יש אי רציפות סליקה.
, בנקודות אלו לגרעין דיריכלה יש אי רציפות סליקה. - זה נכון כיוון שפרט לנקודות אלו מדובר בפונקציה רציפה.
- כמו כן, גרעין דיריכלה מחזורי
 כיוון שהוא סכום של פונקציות מחזוריות
כיוון שהוא סכום של פונקציות מחזוריות  .
.
- נחשב את האינטגרל על גרעין דיריכלה:
- ראשית, לכל
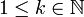 מתקיים:
מתקיים:
- לכן נקבל:
הסכומים החלקיים של טור פוריה
- תהיה נקודה x, נביט בסדרת הסכומים החלקיים של טור הפוריה המתאים לפונקציה
 שהיא מחזורית
שהיא מחזורית  :
:
- נציב את מקדמי פוריה ונקבל כי:
- זה בעצם גרעין דיריכלה, כלומר קיבלנו כי:
- שימו לב ששינוי מספר סופי של נקודות לא משפיע על האינטגרל, ולכן נקודות אי הרציפות הסליקות של גרעין דיריכלה לא פוגעות בהוכחה.
- טענה: תהי
 פונקציה מחזורית
פונקציה מחזורית  . אזי לכל
. אזי לכל 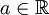 מתקיים כי:
מתקיים כי:
- כלומר, השטח מתחת לגרף הפונקציה שווה על כל קטע באורך
 .
.
- הוכחה:
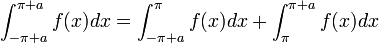
- נבצע הצבה
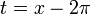 באינטגרל השני ונקבל:
באינטגרל השני ונקבל: 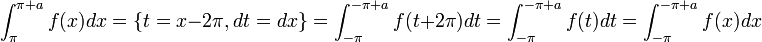
- ביחד נקבל כי:
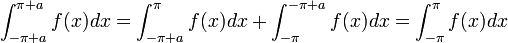
- נחזור לסכומים החלקיים ונבצע הצבה:
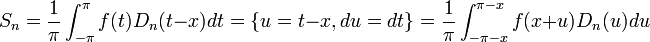
- כיוון שגרעין דיריכלה ו
 הן מחזוריות, נקבל:
הן מחזוריות, נקבל: 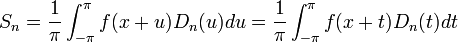
הרצאה 3 התכנסות נקודתית של טורי פוריה
סימונים והגדרות
- נסמן את הגבול החד צדדי מימין ב
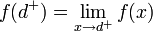 .
. - נסמן את הגבול החד צדדי משמאל ב
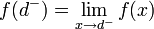 .
. - שימו לב: אם הפונקציה רציפה למקוטעין, הערכים הללו תמיד מוגדרים.
- נגדיר את הנגזרת הימנית ע"י
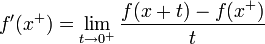 .
. - נגדיר את הנגזרת השמאלית ע"י
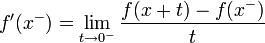 .
. - שימו לב: ייתכן ש
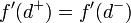 אך הפונקציה אינה גזירה בd. זה יקרה אם היא לא רציפה בנקודה.
אך הפונקציה אינה גזירה בd. זה יקרה אם היא לא רציפה בנקודה.
דוגמא:
- נביט בפונקציה
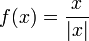
- מתקיים כי
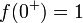 , ו
, ו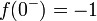 .
. - כמו כן מתקיים כי
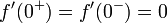 .
.
כמובן שהפונקציה אינה רציפה ואינה גזירה ב0.
משפט דיריכלה - התכנסות נקודתית של טור פוריה
- תהי
 פונקציה מחזורית
פונקציה מחזורית  , רציפה למקוטעין כך שבכל נקודה הנגזרות החד צדדיות שלה קיימות וסופיות.
, רציפה למקוטעין כך שבכל נקודה הנגזרות החד צדדיות שלה קיימות וסופיות. - אזי לכל
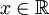 הטור עם מקדמי הפוריה של
הטור עם מקדמי הפוריה של  מתכנס:
מתכנס:
- בפרט, בכל נקודה בה הפונקציה רציפה טור הפוריה מתכנס נקודתית לפונקציה, ובכל נקודה בה יש אי רציפות קפיצתית טור הפוריה מתכנס לממוצע הגבולות מימין ומשמאל.
הוכחה
- תהי נקודה
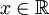 .
. - נביט בפונקציה
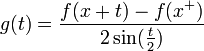
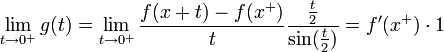
- כיוון שהנגזרות החד צדדיות קיימות וסופיות, קיבלנו ש
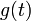 רציפה למקוטעין בקטע
רציפה למקוטעין בקטע ![[0,\pi]](/images/math/e/1/8/e1868564b62b4e2f1c063321df289469.png) .
. - לפי למת רימן-לבג נובע כי:
- כלומר:
- כיוון ש
- נובע כי:
- באופן דומה לחלוטין ניתן להוכיח כי:
- ולכן סה"כ נקבל כי:
דוגמאות
דוגמא 1
- תהי
 ההמשך המחזורי של
ההמשך המחזורי של 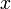 .
.
- כיוון שf רציפה למקוטעין ובעלת נגזרות חד צדדיות קיימות (כולן שוות 1), תנאי משפט דיריכלה מתקיימים.
- כיוון שf הינה אי-זוגית, לכל
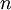 מתקיים כי
מתקיים כי 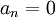 .
.
- כעת נחשב את המקדמים של הסינוסים:
- לכן, בכל נקודת רציפות של f, כלומר בכל נקודה
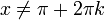 , מתקיים כי:
, מתקיים כי:
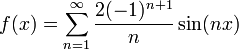 .
.
- בפרט, לכל נקודה
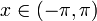 מתקיים כי:
מתקיים כי:
- עבור נקודות אי הרציפות (הקפיצתיות), מתקיים כי הממוצע בין הגבולות החד צדדיים הוא אפס.
- קל לראות שאכן לכל
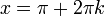 נקבל שטור הפורייה מתכנס לאפס (למעשה כל הסינוסים מתאפסים).
נקבל שטור הפורייה מתכנס לאפס (למעשה כל הסינוסים מתאפסים).
- נציב לדוגמא
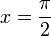 ונקבל:
ונקבל:
- לכל n זוגי הסינוס יתאפס, ולכן נקבל:
- שימו לב שהפעם לא קיבלנו טור חדש בזכות פורייה, כיוון שנקבל בדיוק את אותו הטור אם נציב 1 בטור הטיילור של
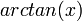 .
.
דוגמא 2
- כעת, תהי
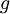 ההמשך המחזורי של
ההמשך המחזורי של 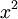 .
. - הפונקציה g הינה רציפה בכל הממשיים.
- הפונקציה g גזירה בכל הממשיים פרט לנקודות
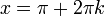 .
. - בנקודות אי הגזירות, הנגזרות החד צדדיות קיימות ושוות ל
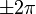 (כיוון שהנגזרת של
(כיוון שהנגזרת של 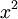 היא
היא 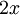 ).
). - סה"כ לפי משפט דיריכלה, טור הפוריה של g מתכנס אליה בכל הממשיים (כיוון שהיא רציפה בכל הממשיים).
- כלומר קיבלנו שלכל
![x\in [-\pi,\pi]](/images/math/c/8/2/c8293d1bbeed341c917b0834713a1b73.png) מתקיים כי:
מתקיים כי:
- שימו לב שאם נגזור איבר איבר את טור הפוריה של
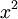 , נקבל את טור הפורייה של
, נקבל את טור הפורייה של 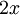 .
. - האם זה מפתיע?
דוגמא 3
- תהי
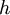 ההמשך המחזורי של הפונקציה
ההמשך המחזורי של הפונקציה ![\begin{cases}x & x\in [0,\pi]\\0 & x\in [-\pi,0)\end{cases}](/images/math/7/b/d/7bdd60b977bad799c8307881d2e07e0e.png)
- שוב, קיבלנו פונקציה רציפה למקוטעין עם נגזרות חד צדדיות קיימות וסופיות.
- נחשב את מקדמי הפורייה:
- סה"כ שלכל
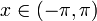 מתקיים כי:
מתקיים כי:
- שימו לב: מצאנו שני טורי פורייה שמתכנסים ל
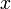 בקטע
בקטע 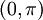 .
. - באופן דומה אפשר להראות שקיימים אינסוף טורי פורייה כאלה.
טור הנגזרת
- תהי
 רציפה בקטע
רציפה בקטע ![[-\pi,\pi]](/images/math/9/1/1/911bebeafbf3d4845e122edfc4f667f8.png) כך שהנגזרת שלה
כך שהנגזרת שלה 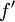 רציפה למקוטעין בקטע.
רציפה למקוטעין בקטע.
שימוש בנוסחאת ניוטון לייבניץ לחישוב האינטגרל המסויים
- שימו לב שמותר לנו להשתמש בנוסחאת ניוטון לייבניץ:
- כיוון שהנגזרת רציפה למקוטעין, אפשר להראות בעזרת לופיטל שהנגזרות החד צדדיות בנקודות אי הגזירות של f קיימות.
- בעצם, זה מראה שf גזירה בקטעים סגורים בהם אפשר להפעיל את נוסחאת ניוטון לייבניץ.
- אם נחשב את האינטגרל על הנגזרת בכל הקטעים הסגורים, ערכי f יצטמצמו, פרט לקצוות.
- לדוגמא:
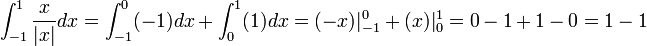
- כלומר קיבלנו כי
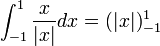 , כאשר
, כאשר 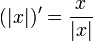
חישוב מקדמי טור הפורייה של הנגזרת
- נסמן את מקדמי הפורייה של
 ב
ב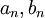
- נחשב את מקדמי הפורייה של הנגזרת, נסמן אותם ב
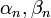 :
:
- כלומר, בתנאים הנתונים, אם טור הפוריה של f הינו:
- אזי טור הפורייה של הנגזרת הינו:
- במקרה המיוחד בו
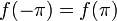 מתקיים כי
מתקיים כי 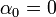 ולכן נקבל את טור הפורייה הפשוט:
ולכן נקבל את טור הפורייה הפשוט:
דוגמאות
דוגמא 1
- נזכר בטור הפורייה של
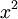 :
:
- נרצה למצוא את מקדמי הפוריה של
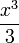 , נסמנם ב
, נסמנם ב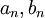 .
.
- לכל
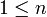 נקבל כי:
נקבל כי:
- כמו כן נחשב את המקדם הראשון:
- נחלץ את המקדמים ונקבל כי טור הפורייה של
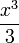 הוא:
הוא:
דוגמא 2
- נחשב את טור הפורייה של
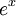 .
. - נסמן את טור הפורייה של
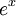 ב:
ב:
- כמובן שהנגזרת במקרה הזה שווה לפונקציה, ולכן יש לה בדיוק אותו טור פורייה.
- מצד שני, טור הפורייה של הנגזרת צריך להיות:
- כאשר
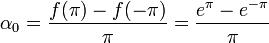
- ביחד נקבל את המשוואות:
- נציב את המשוואה השלישית בשנייה ונקבל:
- ולכן
- סה"כ קיבלנו כי טור הפורייה של
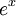 הינו:
הינו:
- כיוון שלהמשך המחזורי של
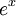 יש אי רציפות קפיצתית ב
יש אי רציפות קפיצתית ב , טור הפורייה שם מתכנס לממוצע
, טור הפורייה שם מתכנס לממוצע 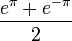
- כלומר, אם נציב
 נקבל:
נקבל:
- נפשט:
הרצאה 4 - התכנסות במ"ש ושיוויון פרסבל
תנאי להתכנסות במ"ש של טור פורייה
- תהי
 רציפה בקטע
רציפה בקטע ![[-\pi,\pi]](/images/math/9/1/1/911bebeafbf3d4845e122edfc4f667f8.png) המקיימת
המקיימת 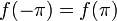 , כך ש
, כך ש 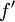 רציפה למקוטעין.
רציפה למקוטעין. - אזי טור הפורייה של
 מתכנס אליה במ"ש בכל הממשיים.
מתכנס אליה במ"ש בכל הממשיים.
- לפי משפט דיריכלה ידוע כי טור הפורייה של ההמשך המחזורי של f מתכנס אליה בכל נקודה.
- נסמן את טור הפורייה ב
- ברור כי
- לפי מבחן ה-M של ויירשטראס, מספיק להוכיח שטור המספרים מימין מתכנס על מנת להסיק שטור הפורייה מתכנס במ"ש.
- נסמן את מקדמי פורייה של הנגזרת ב
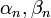 .
. - כבר חישבנו ש:
- לכן ביחד נקבל כי
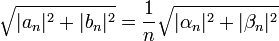
- לפי אי שיוויון קושי שוורץ, נקבל כי לכל n מתקיים:
- לפי אי שיוויון בסל, אנו יודעים כי הטור
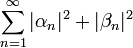 מתכנס, כיוון שמדובר במקדמי פורייה של
מתכנס, כיוון שמדובר במקדמי פורייה של 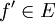 .
.
- (זכרו שמותר להניח כי
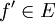 על ידי שינוי מספר סופי של נקודות שלא משפיעות על חישוב מקדמי הפורייה.)
על ידי שינוי מספר סופי של נקודות שלא משפיעות על חישוב מקדמי הפורייה.)
- (זכרו שמותר להניח כי
- לכן
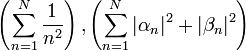 חסומות כסדרות סכומים חלקיים של טורים מתכנסים.
חסומות כסדרות סכומים חלקיים של טורים מתכנסים. - לכן סה"כ
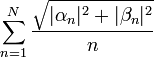 חסומה, ולכן הטור האינסופי המתאים לה מתכנס.
חסומה, ולכן הטור האינסופי המתאים לה מתכנס.
- סה"כ קיבלנו כי
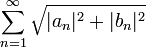 מתכנס.
מתכנס. - לכן בוודאי גם הטורים הקטנים יותר
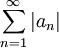 ו
ו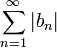 מתכנסים, כפי שרצינו.
מתכנסים, כפי שרצינו.
שיוויון פרסבל
- נביט במערכת האורתונורמלית
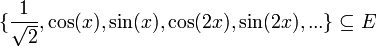 , ותהי
, ותהי 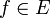 .
. - ידוע לנו כי
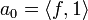 , ולכן
, ולכן 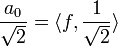
- נסמן את סדרת הסכומים החלקיים של טור הפורייה המתאים לפונקציה f ב
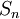 .
. 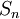 היא ההיטל של
היא ההיטל של  על הקבוצה האורתונורמלית
על הקבוצה האורתונורמלית 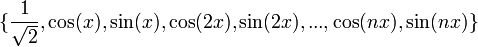
- אכן
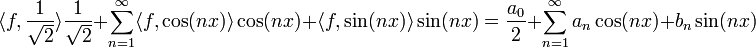
- אכן
- נזכור כי
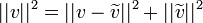
- לכן
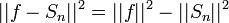 .
.
- לכן
- כמו כן, נזכור כי
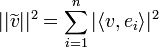
- לכן
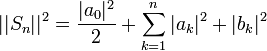
- לכן
- אי שיוויון בסל אומר כי
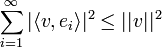
- כלומר:
- משפט שיוויון פרסבל אומר שבעצם מתקיים שיוויון:
- אם נוכיח ש
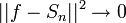 , נסיק כי
, נסיק כי 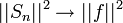 וזהו בדיוק שיוויון פרסבל.
וזהו בדיוק שיוויון פרסבל.
הוכחת שיוויון פרסבל כאשר טור הפורייה מתכנס במ"ש
- תהי
 רציפה בקטע
רציפה בקטע ![[-\pi,\pi]](/images/math/9/1/1/911bebeafbf3d4845e122edfc4f667f8.png) המקיימת
המקיימת 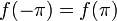 , כך שהנגזרת שלה
, כך שהנגזרת שלה 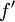 רציפה למקוטעין.
רציפה למקוטעין. - נסמן
![d_n=\sup_{[-\pi,\pi]}|f-S_n|](/images/math/8/2/6/826174f7341a00850b6ac608c6f1c73c.png)
- הוכחנו כי טור הפורייה של f מתכנס אליה במ"ש, כלומר
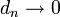 .
. - לכן
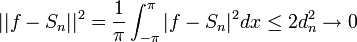
דוגמא
- הפונקציה
 מקיימת את דרישות המשפט.
מקיימת את דרישות המשפט. - נזכור כי טור הפורייה שלה הוא:
- לכן לפי שיוויון פרסבל נקבל כי:
- ולכן:
הוכחת שיוויון פרסבל במקרה הכללי
- תהי
 , אנחנו מעוניינים להוכיח כי
, אנחנו מעוניינים להוכיח כי 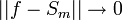 .
. - נבנה סדרת פונקציות
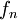 רציפות בקטע
רציפות בקטע ![[-\pi,\pi]](/images/math/9/1/1/911bebeafbf3d4845e122edfc4f667f8.png) המקיימות
המקיימות 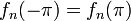 , כך שהנגזרות שלהן
, כך שהנגזרות שלהן 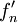 רציפות למקוטעין, המקיימות:
רציפות למקוטעין, המקיימות:
- יהי
 , נבחר
, נבחר 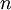 כך ש
כך ש 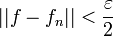 .
. - נסמן ב
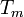 את סדרת הסכומים החלקיים של טור הפורייה של
את סדרת הסכומים החלקיים של טור הפורייה של 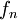 .
. - ראינו כי
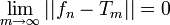 .
.
- כיוון שההיטל הוא הוקטור הקרוב ביותר, נקבל:
- כמו כן,
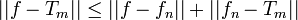
- קיים מקום החל ממנו לכל
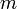 מתקיים כי
מתקיים כי  .
. - לכן החל ממקום זה
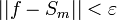 כפי שרצינו.
כפי שרצינו.
בניית סדרת הפונקציות
- f רציפה למקוטעין, ולכן רציפה במ"ש בכל קטע רציפות.
- לכן ניתן לבחור חלוקה
 הכוללת את נקודות אי הרציפות, עם פרמטר חלוקה מספיק קטן כך ש
הכוללת את נקודות אי הרציפות, עם פרמטר חלוקה מספיק קטן כך ש 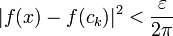 לכל זוג נקודות
לכל זוג נקודות ![x,c_k\in [x_{k-1},x_k]](/images/math/5/c/8/5c8c30cbc0548931f4a435cf00a17f3d.png) .
. - נבחר נקודות כלשהן
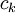 בכל קטע ונביט בפונקצית המדרגות g שבכל תת קטע שווה לקבוע
בכל קטע ונביט בפונקצית המדרגות g שבכל תת קטע שווה לקבוע 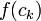 .
. - כעת האינטגרל תמיד קטן מסכום הדרבו העליון:
- לכן אפשר לבנות סדרת פונקציות מדרגות כנ"ל
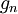 כך ש
כך ש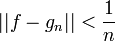
- כעת נגדיר סדרת פונקציות
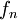 להיות
להיות 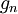 , פרט לשינויים הבאים:
, פרט לשינויים הבאים:
- עבור
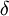 שנקבע בהמשך, נחבר בקו ישר את הנקודות בקצוות המקטעים
שנקבע בהמשך, נחבר בקו ישר את הנקודות בקצוות המקטעים ![[x_k-\delta,x_k]](/images/math/d/2/5/d254852559babcefbfed767b38dde9c7.png) .
. - נגדיר
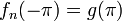 .
. - נחבר בקו ישר את הנקודות בקצה הקטע
![[x_0,x_0+\delta]](/images/math/a/8/0/a800cdf559292b9301d1182668c7b7e8.png) .
.
- עבור
- עבור
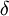 קטנה מספיק,
קטנה מספיק, 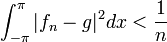 .
.
- סה"כ נקבל כי
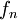 מורכבת מקטעים ישרים המחוברים זה לזה, ולכן מדובר בפונקציה רציפה, בעלת נגזרת רציפה למקוטעין.
מורכבת מקטעים ישרים המחוברים זה לזה, ולכן מדובר בפונקציה רציפה, בעלת נגזרת רציפה למקוטעין.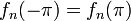
- אכן מתקיים כי
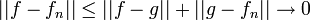
יחידות טור פורייה
הם ישנן שתי פונקציות שונות בעלות אותו טור פורייה?
- תהיינה
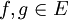 בעלות אותם מקדמי פורייה.
בעלות אותם מקדמי פורייה. - אם טורי הפורייה מתכנסים לפונקציה, ברור שזו אותה הפונקציה, אבל אם לא?
- מקדמי הפורייה של
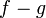 הם אפס, ולכן לפי שיוויון פרסבל:
הם אפס, ולכן לפי שיוויון פרסבל:
- לכן
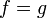 .
.
- שימו לב שעבור סתם פונקציות רציפות למקוטעין, זה אומר ש
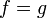 פרט למספר סופי של נקודות.
פרט למספר סופי של נקודות.
האם תתכן פונקציה אחת, בעלת שני טורים טריגונומטריים?
- קנטור הוכיח שאם טור טריגונומטרי שווה לאפס בכל הקטע
![[-\pi,\pi]](/images/math/9/1/1/911bebeafbf3d4845e122edfc4f667f8.png) , אזי כל מקדמי הטור הם אפס.
, אזי כל מקדמי הטור הם אפס. - יותר מאוחר הוכיחו כי אם הטור מתאפס בכל נקודה בקטע פרט לקבוצה בת מנייה של נקודות, עדיין כל מקדמי הטור הם אפס.
- מנשוב מצא ב1916 טור טריגונומטרי שמתכנס לאפס בכל נקודה פרט לקבוצה ממידה אפס של נקודות, אך לא כל מקדמי הטור הם אפס.
הרצאה 5 - תופעת גיבס, טורי הסינוסים והקוסינוסים
תופעת גיבס
- ראינו תנאים בהם טור הפורייה מתכנס במ"ש.
- כעת אנחנו רוצים לחקור מקרים בהם אין התכנסות במ"ש, ונראה כי בהן יש חריגה מיוחדת של סדרת הסכומי החלקיים מן הפונקציה.
- נביט בטור פורייה של הפונקציה x:
- נסמן ב
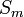 את סדרת הסכומים החלקיים של הטור ונביט ב:
את סדרת הסכומים החלקיים של הטור ונביט ב:
- כעת,
- לכן סה"כ השגיאה בקירוב ע"י הסכומים החלקיים בסדרת הנקודות הללו היא:
- (הערכת האינטגרל נעשית על ידי פיתוח טור הטיילור של הפונקציה, נקבל טור לייבניץ לפיו קל לבצע הערכת שגיאה.)
- כלומר סדרת הסכומים החלקיים עולה משמעותית מעל הפונקציה, כפי שניתן לראות בגרף המצורף.
- אם נחלק את זה בגודל הקפיצה בין הגבולות החד צדדים של ההמשך המחזורי של x בנקודה
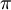 , נקבל בערך
, נקבל בערך 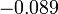 .
.
- לא נוכיח זאת, אבל יחס הטעות הזה בנקודות אי הרציפות נשמר באופן כללי עבור פונקציות בE שנגזרתן רציפה למקוטעין, ונקרא 'תופעת גיבס'.
טור הסינוסים וטור הקוסינוסים
- עבור פונקציה
 הרציפה בקטע
הרציפה בקטע ![[0,\pi]](/images/math/e/1/8/e1868564b62b4e2f1c063321df289469.png) ובעלת נגזרת רציפה למקוטעין, ניתן להשלים אותה לפונקציה
ובעלת נגזרת רציפה למקוטעין, ניתן להשלים אותה לפונקציה 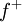 הזוגית בקטע
הזוגית בקטע ![[-\pi,\pi]](/images/math/9/1/1/911bebeafbf3d4845e122edfc4f667f8.png) , או ל
, או ל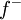 האי זוגית בקטע
האי זוגית בקטע ![[-\pi,\pi]](/images/math/9/1/1/911bebeafbf3d4845e122edfc4f667f8.png) .
.
- את ההמשך הזוגי אפשר לפתח לטור קוסינוסים, שמתכנס במ"ש בקטע
![[0,\pi]](/images/math/e/1/8/e1868564b62b4e2f1c063321df289469.png) . זה נקרא טור הקוסינוסים של הפונקציה
. זה נקרא טור הקוסינוסים של הפונקציה  .
. - הוכחה:
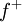 רציפה ב
רציפה ב![[-\pi,\pi]](/images/math/9/1/1/911bebeafbf3d4845e122edfc4f667f8.png) , בעלת נגזרת רציפה למקוטעין, ומתקיים כמובן ש
, בעלת נגזרת רציפה למקוטעין, ומתקיים כמובן ש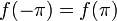 .
.
- את ההמשך האי זוגי אפשר לפתח לטור סינוסים, שמתכנס אל הפונקציה בקטע
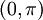 . זה נקרא טור הסינוסים של הפונקציה
. זה נקרא טור הסינוסים של הפונקציה  .
. - אם
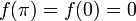 אזי טור הסינוסים מתכנס במ"ש בקטע
אזי טור הסינוסים מתכנס במ"ש בקטע ![[0,\pi]](/images/math/e/1/8/e1868564b62b4e2f1c063321df289469.png) .
. - הוכחה:
 רציפה כיוון ש
רציפה כיוון ש , ומתקיים כי
, ומתקיים כי 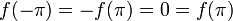 .
.
- חישוב המקדמים:
- עבור טור הקוסינוסים:
- עבור טור הסינוסים:
דוגמאות
- נחשב טור קוסינוסים של
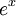 :
:
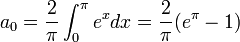
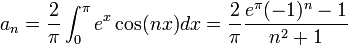
- הטור מתכנס במ"ש לפונקציה בקטע
![[0,\pi]](/images/math/e/1/8/e1868564b62b4e2f1c063321df289469.png) :
:
- לכן מותר לבצע אינטגרציה איבר איבר, נחשב את
 בשני הצדדים ונקבל:
בשני הצדדים ונקבל:
- נציב למשל
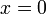 ונקבל את השיוויון:
ונקבל את השיוויון:
- נחשב טור סינוסים של
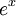 :
:
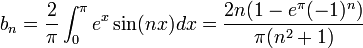
- הטור מתכנס בקטע
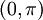 :
:
- נחשב טור סינוסים של
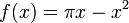 .
. - שימו לב:
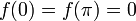 .
.
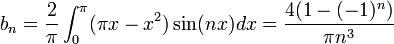
- לכן הטור מתכנס במ"ש בקטע
![[0,\pi]](/images/math/e/1/8/e1868564b62b4e2f1c063321df289469.png) :
:
- לכן מותר לבצע אינטגרציה איבר איבר, נחשב את
 בשני הצדדים ונקבל:
בשני הצדדים ונקבל:
- שימו לב שלא מדובר בטור טריגונומטרי.
הרצאה 6 - משוואת החום על טבעת, התמרת פורייה
משוואת החום על טבעת
- נביט במד"ח החום על מוט עבור הפונקציה
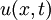 :
:
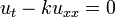
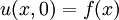 (תנאי התחלה)
(תנאי התחלה)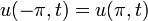 (תנאי שפה)
(תנאי שפה)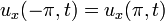 (תנאי שפה)
(תנאי שפה)- כאשר
![x\in[-\pi,\pi]](/images/math/c/8/2/c8293d1bbeed341c917b0834713a1b73.png) , ו
, ו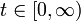
- על מנת להבין את תנאי השפה, אפשר לחשוב על הבעייה במובן שהמוט הוא מעגלי.
- נחפש פתרון מהצורה
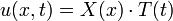 .
. - נציב במד"ח את הניחוש, ונקבל:
- נניח שהצדדים שונים מאפס ונחלק:
- כיוון שכל צד תלוי במשתנה אחר, הדרך היחידה לקבל שיוויון היא אם שני הצדדים קבועים.
- נביט בפתרונות עבור קבוע שלילי:
- כעת נפתור את המד"רים בנפרד:
- שימו לב שאנו בוחרים את השמות של הקבועים בצורה מיוחדת לקראת הפתרון בהמשך.
- עבור
 :
:
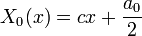 , ועל מנת לקיים את תנאי השפה נקבל כי
, ועל מנת לקיים את תנאי השפה נקבל כי 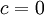
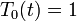 (הקבוע יבלע בקבוע של
(הקבוע יבלע בקבוע של 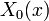 )
)
- עבור
- עבור
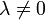 :
:
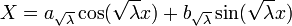
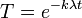 (הקבוע חסר כי הוא יבלע בקבועים האחרים כאשר נכפול ב
(הקבוע חסר כי הוא יבלע בקבועים האחרים כאשר נכפול ב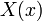 )
)
- עבור
- ע"י הצבה ניתן לוודא שעבור
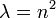 הפונקציות לעיל מקיימות את תנאי השפה.
הפונקציות לעיל מקיימות את תנאי השפה. - גם צירוף לינארי שלהן יהווה פתרון כיוון שהמד"ח הומוגנית ותנאי השפה הומוגניים.
- צירוף לינארי אינסופי יהווה פתרון לבעייה אם טורי הנגזרות יתכנסו במ"ש (ולכן יהיה מותר לגזור איבר איבר).
- לכן אנו מחפשים פתרון כללי מהצורה:
- כל שנותר לנו לעשות הוא למצוא את הקבועים
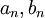 .
. - נציב כעת בתנאי ההתחלה
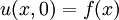 ונקבל בעצם את טור הפורייה:
ונקבל בעצם את טור הפורייה:
- אנחנו יכולים לפתור משוואה זו בהנתן שf מקיימת את תנאי משפט דיריכלה.
- מדוע זה יהיה פתרון?
- נזכור שמקדמי הפורייה שואפים לאפס.
- בזכות האקספוננט, טור זה ונגזרותיו אכן יתכנסו במ"ש עבור
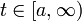 לכל
לכל 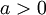 ולכל
ולכל ![x\in[-\pi,\pi]](/images/math/c/8/2/c8293d1bbeed341c917b0834713a1b73.png) .
. - לכן מותר לגזור איבר איבר, ואכן מדובר בפתרון של המד"ח.
התמרת פורייה
טור פורייה המרוכב
- לא קשה לוודא כי
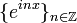 מהווה קבוצה אורתונורמלית בE אם נעדכן מעט את המכפלה הפנימית:
מהווה קבוצה אורתונורמלית בE אם נעדכן מעט את המכפלה הפנימית:
- תהי
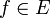 , שאלה שעולה באופן טבעי היא האם:
, שאלה שעולה באופן טבעי היא האם:
- כאשר אנו מגדירים את הסכום ממינוס אינסוף עד אינסוף באופן הבא:
- נסמן את מקדמי פורייה הרגילים ב
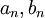 .
.
- נשים לב כי עבור
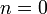 נקבל:
נקבל:
- כעת עבור
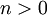 מתקיים:
מתקיים:
- (שימו לב: הi יצא מהצד הימני של המכפלה הפנימית עם מינוס)
- כלומר, טור פורייה המרוכב הוא בדיוק טור פורייה הרגיל!
הכללה לפונקציות שאינן מחזוריות
- טורי פורייה עזרו לנו לחקור פונקציות בקטע
![[-\pi,\pi]](/images/math/9/1/1/911bebeafbf3d4845e122edfc4f667f8.png) .
. - בהנתן גל
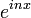 , מצאנו את ה'אמפליטודה' שלו (המקדם):
, מצאנו את ה'אמפליטודה' שלו (המקדם):
- (שימו לב - המכפלה הפנימית מצמידה את הפונקציה מימין, ולכן קיבלנו
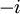 ).
).
- מחשבה הגיונית היא שאם נרצה לחקור פונקציות בכל הממשיים, עבור גל
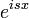 נמצא את ה'אמפליטודה':
נמצא את ה'אמפליטודה':
=\frac{1}{2\pi}\int_{-\infty}^\infty f(x)e^{-isx}dx](/images/math/9/3/7/93777760c24086ac05953f376cf0a6d0.png) .
.
- כאשר האינטגרל מתכנס, הפונקציה
](/images/math/7/e/1/7e1b61e8fc25603bc4e801977072e308.png) נקראת התמרת פורייה של הפונקציה
נקראת התמרת פורייה של הפונקציה  .
. - הערה - המקדם
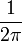 לעיתים אינו מופיע בהגדרת ההתמרה. אנחנו נראה בהמשך שיש לו קשר להתמרה ההפוכה.
לעיתים אינו מופיע בהגדרת ההתמרה. אנחנו נראה בהמשך שיש לו קשר להתמרה ההפוכה.
- הערות כלליות:
- נסמן בדר"כ את ההתמרה של f ב
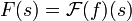 .
. 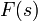 מייצגת את האמפליטודה בכל תדר, ולכן נהוג לומר שהיא מוגדרת ב'מרחב התדר'.
מייצגת את האמפליטודה בכל תדר, ולכן נהוג לומר שהיא מוגדרת ב'מרחב התדר'.- לעומת זאת,
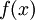 מייצגת את גובה הפונקציה בכל נקודה בזמן, ונהוג לומר שהיא מוגדרת ב'מרחב הזמן'.
מייצגת את גובה הפונקציה בכל נקודה בזמן, ונהוג לומר שהיא מוגדרת ב'מרחב הזמן'. - לכל תדר
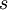 יש שני גלים שמייצגים אותו,
יש שני גלים שמייצגים אותו, 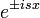 .
. - כפי שלמדנו, באמצעות שני הגלים ניתן לייצג כל 'פאזה'.
- נסמן בדר"כ את ההתמרה של f ב
- נסמן ב
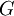 את אוסף הפונקציות
את אוסף הפונקציות 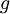 הרציפות למקוטעין ב
הרציפות למקוטעין ב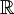 , עבורן האינטגרל הלא אמיתי מתכנס
, עבורן האינטגרל הלא אמיתי מתכנס 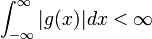 .
. - לכל
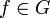 התמרת הפורייה מוגדרת בכל הממשיים.
התמרת הפורייה מוגדרת בכל הממשיים.
- הוכחה:
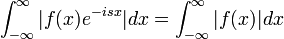 מתכנס.
מתכנס.- כיוון שהאינטגרל המגדיר את
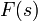 מתכנס בהחלט, הוא מתכנס.
מתכנס בהחלט, הוא מתכנס.
דוגמאות
- נמצא את
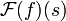 עבור
עבור 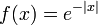 .
.
- שימו לב - השתמשנו בעובדה ש
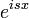 חסומה, ואילו
חסומה, ואילו 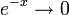 כאשר
כאשר  .
. - לכן סה"כ קיבלנו כי
 = \frac{1}{\pi(1+s^2)}](/images/math/2/a/4/2a42a2fc78cd24dbd00e4aa5fdafdb01.png)
- נמצא את התמרת הפורייה של
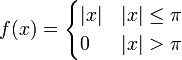
- שימו לב: חישוב האינטגרל שגוי עבור
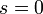 , ניתן להציבו בנוסחא המקורית של האינטגרל או להשתמש ברציפות ההתמרה, שנלמד בהמשך.
, ניתן להציבו בנוסחא המקורית של האינטגרל או להשתמש ברציפות ההתמרה, שנלמד בהמשך.
הרצאה 7 - תכונות של התמרות פורייה
תכונות ההתמרה
- תהי
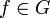 אזי
אזי ](/images/math/2/c/5/2c5661e27dac90f79985bec8b323dfcd.png) רציפה במ"ש ב
רציפה במ"ש ב .
.
- הוכחה:
- יהי
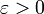 . כיוון ש
. כיוון ש 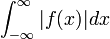 מתכנס, קיים
מתכנס, קיים  עבורו
עבורו 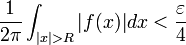
- עבור
 מתקיים כי
מתקיים כי 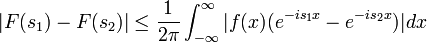
- כמובן ש
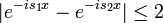 ולכן בתחום
ולכן בתחום 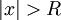 האינטגרל הנ"ל קטן מ
האינטגרל הנ"ל קטן מ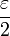 .
. - נותר להוכיח שעבור
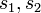 מספיק קרובים מתקיים כי
מספיק קרובים מתקיים כי 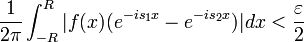
- נראה כי
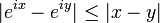 .
.
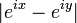 הוא המרחק בין שתי נקודות על מעגל היחידה.
הוא המרחק בין שתי נקודות על מעגל היחידה.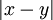 הוא הזווית בינהן, כלומר אורך הקשת בינהן.
הוא הזווית בינהן, כלומר אורך הקשת בינהן.- אורך הקשת בוודאי גדול או שווה למרחק הישר בין שתי הנקודות.
- לכן
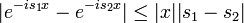
- כיוון ש
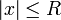 והפונקציה
והפונקציה  חסומה בתחום זה, עבור
חסומה בתחום זה, עבור 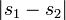 מספיק קטן נקבל את הדרוש.
מספיק קטן נקבל את הדרוש.
- רשימת תכונות נוספות של ההתמרה:
![\mathcal{F}[f+a\cdot g] = \mathcal{F}[f]+a\mathcal{F}[g]](/images/math/1/b/0/1b0ef3642597d0ea874acacc5c9a2149.png)
 = \overline{\mathcal{F}[f](s)}](/images/math/4/5/5/455abd638020b9193c2b4aacacd62419.png)
- אם
 ממשית וזוגית, גם
ממשית וזוגית, גם ](/images/math/7/e/1/7e1b61e8fc25603bc4e801977072e308.png) ממשית וזוגית.
ממשית וזוגית.
- הזזה במרחב הזמן:
- אם
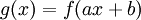 , אזי
, אזי ](/images/math/d/7/9/d79c3fb9a832d8837fcb3a69f7bdca78.png)
- אם
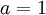 אז נקבל שהזזה במרחב הזמן שקולה לסיבוב במרחב התדר (כפל ב
אז נקבל שהזזה במרחב הזמן שקולה לסיבוב במרחב התדר (כפל ב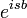 משנה את הזוית).
משנה את הזוית).
- הזזה במרחב התדר:
 = \mathcal{F}[f](s-b)](/images/math/a/6/4/a64c67ea81661afc9d44f88118f00093.png)
- באופן דומה, קיבלנו שסיבוב בזמן שקול להזזה בתדר.
- התמרת הנגזרת:
- נניח
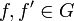 ונניח כי
ונניח כי 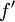 רציפה ומתקיים כי
רציפה ומתקיים כי 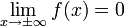 , אזי:
, אזי: =is\mathcal{F}[f](s)](/images/math/8/3/a/83a17f1df841167d6379ce0c5be0ea2e.png)
- הוכחה:
 = \frac{1}{2\pi}\int_{-\infty}^{\infty} f'(x)e^{-isx}dx](/images/math/f/3/1/f31b4c29973ce0e038001220e5a4f14e.png)
- נבצע אינטגרציה בחלקים ונקבל כי
 = \frac{1}{2\pi}(fe^{-isx})_{-\infty}^{\infty} + \frac{is}{2\pi} \int_{-\infty}^{\infty} f(x)e^{-isx}dx](/images/math/6/f/3/6f330d3a09eeed73802fc6a07bbc4198.png) .
.- כיוון ש
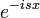 חסומה, יחד עם הנתון נובע כי
חסומה, יחד עם הנתון נובע כי 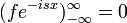 .
. - לכן סה"כ קיבלנו כי
=is\mathcal{F}[f](s)](/images/math/8/3/a/83a17f1df841167d6379ce0c5be0ea2e.png)
- נגזרת ההתמרה:
- תהי
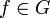 רציפה כך ש
רציפה כך ש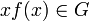 אזי:
אזי: =i\frac{d}{ds}\mathcal{F}[f](s)](/images/math/2/8/f/28fe8d5528346f2342a1eafd67f49565.png)
- הוכחה:
 = i \frac{d}{ds} \frac{1}{2\pi}\int_{-\infty}^{\infty} f(x)e^{-isx}dx = \frac{i}{2\pi}\int_{-\infty}^{\infty} f(x)\frac{d}{ds}e^{-isx}dx = \frac{-i^2}{2\pi}\int_{-\infty}^{\infty} xf(x)e^{-isx} = \mathcal{F}[xf(x)](s)](/images/math/e/8/1/e81158ba9f4d8f867b1be69ba43808bd.png)
- אנחנו צריכים להצדיק את ההכנסה של הנגזרת אל תוך האינטגרל:
- נסמן
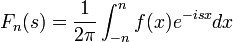
- ברור ש
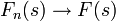 , נוכיח שסדרת הנגזרות מתכנסת במ"ש ולכן מתכנסת לנגזרת של
, נוכיח שסדרת הנגזרות מתכנסת במ"ש ולכן מתכנסת לנגזרת של 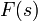 .
. - עבור אינטגרל סופי מותר להחליף את סדר הנגזרת והאינטגרל בזכות פוביני.
- אכן
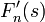 מתכנסות במ"ש כיוון שהאינטגרל
מתכנסות במ"ש כיוון שהאינטגרל 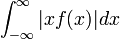 מתכנס, והרי
מתכנס, והרי 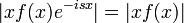 ואכן אינו תלוי בs.
ואכן אינו תלוי בs.
- נסמן
דוגמאות
- ראינו כי
 = \frac{1}{\pi(1+s^2)}](/images/math/2/a/4/2a42a2fc78cd24dbd00e4aa5fdafdb01.png)
- לכן על ידי הזזה בזמן נקבל כי:
- נסמן
![F(s)=\mathcal{F}[e^{-x^2}]](/images/math/d/a/4/da48c19515110db778279941d7ef2843.png) .
. - כעת
![\mathcal{F}[xe^{-x^2}] = iF'](/images/math/8/9/0/890a87dd9f083ab8cbc176df4a0f73e7.png) לפי הנוסחא של נגזרת ההתמרה.
לפי הנוסחא של נגזרת ההתמרה. - מצד שני,
![\mathcal{F}[-2xe^{-x^2}] = isF](/images/math/a/d/2/ad293a137a574251fbe884aac4997965.png) לפי הנוסחא של התמרת הנגזרת.
לפי הנוסחא של התמרת הנגזרת. - ביחד נקבל כי
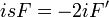 , ולכן
, ולכן 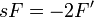 .
. - נפתור את המד"ר:
- נכפול בגורם אינטגרציה
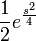 ונקבל
ונקבל 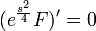
- לכן
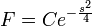
- נציב
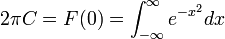 , נחשב אינטגרל מפורסם זה בהמשך.
, נחשב אינטגרל מפורסם זה בהמשך.
- נכפול בגורם אינטגרציה
הרצאה 8 - התמרה הפוכה
- בטורי פורייה, מקדמי הפורייה היו האמפליטודות של התדרים, וכאשר סכמנו את הגלים קיבלנו חזרה את הפונקציה לפי משפט דיריכלה.
- כעת התדרים שלנו הם כל הממשיים, ולכן הסכימה שלהם היא בעצם אינטגרל.
- האמפליטודה של כל תדר מרוכב
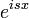 היא התמרת הפורייה
היא התמרת הפורייה 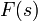 , ולכן אנחנו מצפים לקבל:
, ולכן אנחנו מצפים לקבל:
- משפט ההתמרה ההפוכה:
- תהי
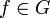 , אזי בכל נקודה בה קיימות הנגזרות החד צדדיות מתקיים כי:
, אזי בכל נקודה בה קיימות הנגזרות החד צדדיות מתקיים כי: e^{isx}ds](/images/math/5/9/a/59ae7376c16b9892bf6be905c5c6c81a.png)
- שימו לב שהאינטגרל
e^{isx}ds](/images/math/6/e/2/6e26264bc2a8d1e493ec8c92694fd0fb.png) לא חייב להתכנס, אבל אם הוא מתכנס הוא שווה לגבול לעיל.
לא חייב להתכנס, אבל אם הוא מתכנס הוא שווה לגבול לעיל.
- תהי
דוגמא
- ראינו ש
![\mathcal{F}[e^{-x^2}] = Ce^{-\frac{s^2}{4}} =\frac{1}{2\pi}\int_{-\infty}^\infty e^{-x^2}e^{-isx}dx](/images/math/4/1/1/41130b6b42bce0811209a7aa84fb397b.png)
- כיוון ש
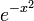 רציפה וגזירה, וכיוון ש
רציפה וגזירה, וכיוון ש 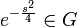 לפי משפט ההתמרה ההפוכה נקבל כי:
לפי משפט ההתמרה ההפוכה נקבל כי:
- כלומר
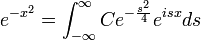
- נציב
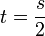 ונקבל:
ונקבל:
- ולכן
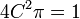 , ומכאן
, ומכאן 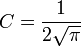
- נזכור בנוסף שראינו כי
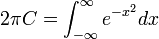 .
. - לכן נובע כי
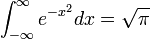
דוגמא
- נביט ב
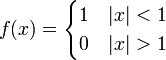
 = \frac{sin(s)}{\pi s}](/images/math/0/d/e/0dee0c2d447cbbcf2eb44c18242e72fb.png)
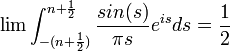 (הצבנו x=1, הנקודה בה f אינה רציפה).
(הצבנו x=1, הנקודה בה f אינה רציפה).
הקדמה לקראת הוכחת משפט ההתמרה ההפוכה
- כעת נוכיח מספר טענות הדרושות לנו לצורך הוכחת משפט ההתמרה ההפוכה.
למת רימן-לבג
- ראינו גרסא של למת רימן-לבג עבור טורי פוריה, לפי מקדמי הפורייה שואפים לאפס.
- כעת ננסח ונוכיח גרסא עבור התמרות פורייה:
- תהי
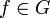 , אזי
, אזי =0](/images/math/7/1/9/7198cb1a9d11057f27c57f31a6d5dc33.png)
- (כלומר, האמפליטודות שואפות לאפס כאשר התדר שואף לאינסוף)
- נוכיח את הלמה:
- צ"ל כי
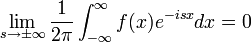
- נשים לב כי
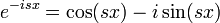 .
. - לכן מספיק לנו להוכיח כי
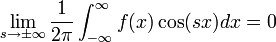 (ההוכחה עבור סינוס דומה).
(ההוכחה עבור סינוס דומה). - כיוון ש
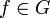 האינטגרל
האינטגרל 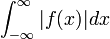 מתכנס.
מתכנס. - לכן קיים
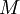 עבורו
עבורו 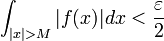 .
. - לכן
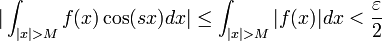
- לכן מספיק לנו להוכיח כי עבור
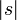 מספיק גדול מתקיים
מספיק גדול מתקיים 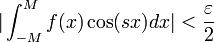
- (עבור
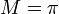 ו
ו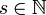 כבר הוכחנו טענה זו בעזרת פרסבל, כעת נשתמש בשיטות אחרות.)
כבר הוכחנו טענה זו בעזרת פרסבל, כעת נשתמש בשיטות אחרות.)
- נשים לב כי בכל קטע מתקיים:
- כיוון ש
 רציפה למקוטעין היא אינטגרבילית ב
רציפה למקוטעין היא אינטגרבילית ב![[-M,M]](/images/math/f/9/b/f9b7329df8a2ac4dd6453f4a08ed77a5.png) .
. - לכן ניתן לבחור פונקצית מדרגות
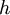 עבורה מתקיים
עבורה מתקיים 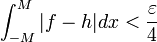 (האינטגרל על פונקצית המדרגות הינו סכום דרבו תחתון מספיק קרוב).
(האינטגרל על פונקצית המדרגות הינו סכום דרבו תחתון מספיק קרוב). - כמו כן מתקיים:
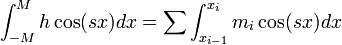
- כיוון שמדובר בסכום סופי של ביטויים ששואפים לאפס, הסכום גם שואף לאפס.
- סה"כ
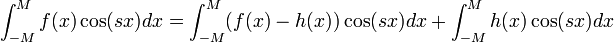
- מתקיים כי
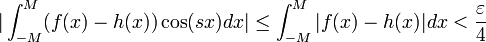
- עבור
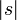 מספיק גדול מתקיים כי
מספיק גדול מתקיים כי 
- מתקיים כי
- סה"כ קיבלנו כי עבור
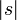 מספיק גדול מתקיים
מספיק גדול מתקיים 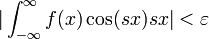
טענת עזר
- תהי
 ותהי x נק' בה הנגזרות החד צדדיות קיימות, אזי:
ותהי x נק' בה הנגזרות החד צדדיות קיימות, אזי:
- נוכיח את הטענה הראשונה, הטענה השנייה דומה.
- נגדיר את הפונקציה
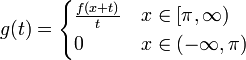
- כיוון ש
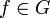 נובע שגם
נובע שגם 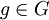 הרי
הרי 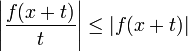 עבור
עבור 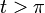 .
. - לכן לפי למת רימן-לבג נובע כי
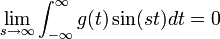
- בפרט מתקיים גבול הסדרה:
- אבל
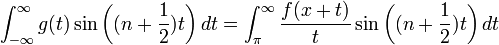
- לכן נותר להוכיח כי
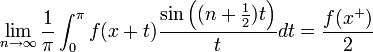
- נגדיר את הפונקציה
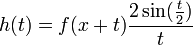 .
.
- אם נתקן את אי הרציפות הסליקה של
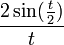 נקבל טור טיילור שגזיר אינסוף פעמים.
נקבל טור טיילור שגזיר אינסוף פעמים. - לכן הפוקנציה
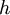 רציפה למקוטעין ובעלת נגזרות חד צדדיות קיימות.
רציפה למקוטעין ובעלת נגזרות חד צדדיות קיימות.
- אם נתקן את אי הרציפות הסליקה של
- כעת נשים לב כי:
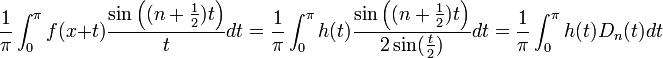
- לפי ההוכחה של משפט דיריכלה להתכנסות טורי פורייה, הגבול של הביטוי הזה שווה ל
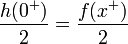 .
.
דוגמא
- טענה:
- הוכחה:
- ראשית, אנו יודעים כי האינטגרל מתכנס לפי מבחן דיריכלה לאינטגרלים לא אמיתיים.
- לכן מתקיים כי
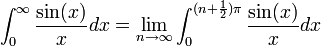
- נבצע הצבה
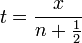 ונקבל כי:
ונקבל כי:
- עבור
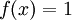 , לפי הוכחת טענת העזר נקבל כי הגבול הוא
, לפי הוכחת טענת העזר נקבל כי הגבול הוא 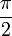
הוכחת משפט ההתמרה ההפוכה
e^{isx}ds = \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\left[\frac{1}{2\pi}\int_{-\infty}^\infty f(y)e^{-isy}dy\right]e^{isx}ds=](/images/math/f/3/b/f3bb5843838124d22ef6966c81d4cc8a.png)
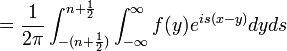
- נחליף את סדר האינטגרציה (הצדקה בהמשך), ונקבל:
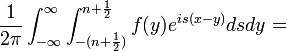
![\frac{1}{2\pi}\int_{-\infty}^\infty f(y) \left[\frac{e^{is(x-y)}}{i(x-y)}\right]_{-(n+\frac{1}{2})}^{n+\frac{1}{2}} dy =](/images/math/f/6/9/f699cd30045eb055a415f6c35c7e8c2a.png)
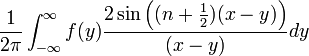
- נציב
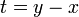 ונקבל:
ונקבל: 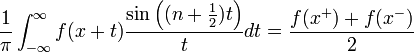
כאשר המעבר האחרון הוא בזכות טענת העזר לעיל.
הצדקת החלפת סדר האינטגרציה
- נביט בסדרה
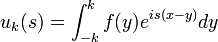 , שמתכנסת כמובן ל
, שמתכנסת כמובן ל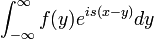
- מתקיים כי
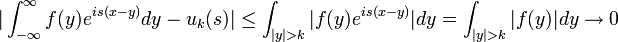
- (נתון כי
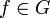 )
)
- (נתון כי
- לכן הסדרה מתכנסת במ"ש ומותר לבצע אינטגרציה איבר איבר:
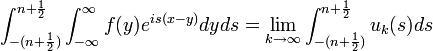
- לפי פוביני מותר לנו להחליף את סדר האינטגרציה ונקבל כי
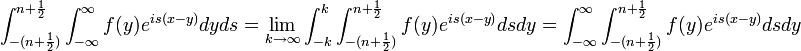
- שימו לב שהאינטגרל הלא אמיתי אכן מתכנס (כפי שהוכחנו לעיל) ולכן שווה לגבול.
הרצאה 9 - קונבולוציה, משוואת החום על מוט אינסופי
- תהיינה
 פונקציות, נגדיר את הקונבולוציה ביניהן להיות:
פונקציות, נגדיר את הקונבולוציה ביניהן להיות:
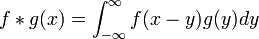 .
.
- מוטיבציה לדוגמא:
- אם
 הן פונקציות צפיפות של משתנים מקריים, מהי פונקציית הצפיפות של סכום המשתנים?
הן פונקציות צפיפות של משתנים מקריים, מהי פונקציית הצפיפות של סכום המשתנים? - הסיכוי שסכום המשתנים יהיה x, הוא סכום מכפלות הסיכויים שמשתנה אחד יהיה שווה y והשני יהיה שווה x-y.
- אם
- הקונבולוציה היא אבלית:
- שימו לב: בנושא זה נבצע החלפת סדר אינטגרציה, אך לא נצדיק החלפה זו כיוון שהיא דורשת העמקה רבה.
- ניתן להעמיק ע"י קריאה בספר Fourier Analysis של T.W.Korner
- משפט הקונבולוציה:
- תהיינה
 רציפות וחסומות אזי
רציפות וחסומות אזי ![\mathcal{F}[f*g] = 2\pi \cdot \mathcal{F}[f] \cdot \mathcal{F}[g]](/images/math/c/a/7/ca793a8f1150a4d52e3c55d9de033396.png)
- הסבר המשפט (לא הוכחה מלאה, כיוון שאנו מחליפים סדר אינטגרציה ללא הצדקה):
משוואת החום על מוט אינסופי
- אם פונקצית החום על מוט אינסופי היא
 , היא מקיימת את המשוואה
, היא מקיימת את המשוואה 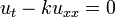 .
. - נניח גם כי תנאי ההתחלה הם
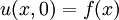 (זה החום בכל נקודה במוט בזמן 0).
(זה החום בכל נקודה במוט בזמן 0).
- נבצע התמרת פורייה של הפתרון לפי המשתנה x:
- נגזור לפי המשתנה t:
- (נניח כי הפתרון מקיים את התנאים שמאפשרים להחליף את סדר הגזירה והאינטגרציה, לא נרחיב על כך בהמשך)
- כיוון ש
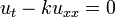 נקבל כי:
נקבל כי:
- נזכר בנוסחאת התמרת הנגזרת
![\mathcal{F}[f']=is\mathcal{F}[f]](/images/math/b/5/2/b52be90de067012bc2fcbd52c3783b5b.png)
- ולכן נקבל כי:
- זו מד"ר פשוטה שפתרונה הוא:
- נציב את תנאי ההתחלה
 ונקבל כי
ונקבל כי
- לכן בעצם מתקיים כי
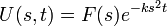
- קיבלנו שההתמרה של הפתרון היא מכפלה של שתי התמרות, ולכן הפתרון הוא הקונבולוציה של שתי הפונקציות המקוריות.
- נחפש את ההתמרה ההפוכה של
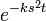
- נזכור כי
![\mathcal{F}[e^{-x^2}] = \frac{1}{2\sqrt{\pi}} e^{-\frac{s^2}{4}}](/images/math/0/f/2/0f2559c31ad99a78b5cf01621dd89870.png)
- נסמן פונקציה זו ב
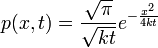
- לכן עבור פתרון מד"ח החום u מתקיים כי:
- ולכן לפי משפט הקונבולוציה מתקיים כי
- שימו לב שהקונבולוציה היא לפי המשתנה x.
- לכן
- שימו לב שבפתרון הסופי מופיעה פונקצית תנאי ההתחלה, ואין צורך לחשב את ההתמרה שלה.
הרצאה 10 - משפט הדגימה של שנון
משפט הדגימה של שנון
- תהי פונקציה f. ברור שבהנתן הערכים של f על השלמים
 לא ניתן להסיק כלום על ערכיה האחרים (אפילו אם היא רציפה וגזירה).
לא ניתן להסיק כלום על ערכיה האחרים (אפילו אם היא רציפה וגזירה). - בפרט אם נדגום באופן דומה את הפונקציה
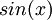 בנקודות
בנקודות 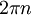 אנחנו עשויים לחשוד שהיא קבועה לחלוטין.
אנחנו עשויים לחשוד שהיא קבועה לחלוטין. - מה יקרה אם נדגום גל בקצב מהיר יותר מהתדר שלו?
- במילים פשוטות, משפט הדגימה של שנון אומר שבהנתן פונקציה שהתדרים שלה חסומים, אם נדגום אותה בקצב מהיר פי 2 מהתדר המקסימלי שלה, נוכל לשחזר אותה לחלוטין.
- כעת ננסח את המשפט במדויק, יחד עם ניסוח התנאים הנחוצים על הפונקציות.
- עד כה דיברנו על תדר כמדד לקצב בו הפונקציה חוזרת על עצמה, כעת נגדיר אותו במדויק:
- בהנתן פונקציה עם מחזור
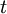 נגדיר את התדר של המחזור להיות
נגדיר את התדר של המחזור להיות  .
. - דוגמאות:
- התדר של
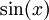 הוא
הוא 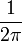
- התדר של
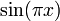 הוא
הוא 
- באופן כללי, התדר של
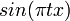 הוא
הוא 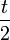 כיוון ש
כיוון ש 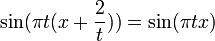
- התדר של
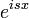 הוא
הוא 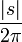 כיוון ש
כיוון ש 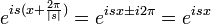
- התדר של
- משפט הדגימה של שנון:
- תהי
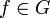 רציפה ובעלת נגזרת חד צדדיות הקיימות בכל נקודה, שתדריה חסומים על ידי
רציפה ובעלת נגזרת חד צדדיות הקיימות בכל נקודה, שתדריה חסומים על ידי 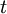 , אזי בהנתן דגימה שלה בתדר
, אזי בהנתן דגימה שלה בתדר 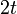 ניתן לשחזר אותה בכל הממשיים (כלומר היא נקבעת באופן יחיד על ידי הדגימות).
ניתן לשחזר אותה בכל הממשיים (כלומר היא נקבעת באופן יחיד על ידי הדגימות). - שימו לב: הכוונה בכך שתדריה של הפונקציה חסומים, היא למעשה ש
=0](/images/math/6/1/f/61f1fb2261353e227d0edab34ef219e0.png) לכל
לכל 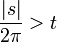 .
.
הוכחת משפט הדגימה
- כיוון שהתמרת הפורייה מתאפסת מחוץ לקטע
![[-2\pi t,2\pi t]](/images/math/9/0/5/90543d4de85c883ab34df8067b5c15a6.png) , ניתן לקבוע כי
, ניתן לקבוע כי
- ובפרט האינטגרל מתכנס.
- לפי משפט ההתמרה ההפוכה, נובע כי
e^{isx}ds](/images/math/3/a/9/3a9144bf0583bff2e53e1f4b7f200b11.png)
- כעת, נתונה לנו סדרת הדגימות בתדר
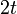 :
:
- נציב אותן בנוסחא שמצאנו לעיל:
- נבצע הצבה
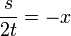 ונקבל:
ונקבל:
- אבל אלה בדיוק מקדמי פוריה (פרט לקבוע
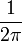 ) של הפונקציה
) של הפונקציה ](/images/math/7/c/1/7c1a88dd4b079d23495887acf57f5306.png) .
. - כיוון שההתמרה חסומה בתדר, עבור
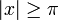 מתקיים כי
מתקיים כי =0](/images/math/e/9/d/e9dd99710ccab32def87fa38548f8ba7.png) (זכרו כי ההתמרה רציפה, ולכן מתאפסת גם בקצוות).
(זכרו כי ההתמרה רציפה, ולכן מתאפסת גם בקצוות). - לכן
](/images/math/7/c/1/7c1a88dd4b079d23495887acf57f5306.png) נקבעת על ידי ערכיה בקטע
נקבעת על ידי ערכיה בקטע 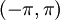 , והם נקבעים באופן יחיד על ידי מקדמי הפורייה (מסקנה מפרסבל).
, והם נקבעים באופן יחיד על ידי מקדמי הפורייה (מסקנה מפרסבל). - לבסוף, כפי שראינו לעיל, הפונקציה f נקבעת באופן יחיד על ידי ההתמרה (בזכות משפט ההתמרה ההפוכה).
הערות
- שימו לב שלא ניתן באופן פרקטי לדגום אות אנלוגי באינסוף נקודות.
- מה יקרה אם נדגום במספר סופי של נקודות ונניח כי הפונקציה ממשיכה באופן מחזורי?
- נקבל פונקציה שאינה שייכת ל
 , כיוון שהאינטגרל שלה לא יכול להתכנס בכל הממשיים.
, כיוון שהאינטגרל שלה לא יכול להתכנס בכל הממשיים. - בהמשך, נראה אנלוגיה למשפט הדגימה של שנון בהתמרת פורייה הבדידה.
הרצאה 11 - התמרת פורייה הבדידה
DFT - Discrete Fourier transform
- תהי סדרת נקודות
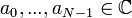 , התמרת הפורייה הבדידה שלה היא סדרת הנקודות
, התמרת הפורייה הבדידה שלה היא סדרת הנקודות 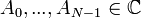 המוגדרת ע"י:
המוגדרת ע"י:
- שימו לב שכמות הפעולות הנדרשות לחישוב ההתמרה באופן ישיר היא סדר גודל של
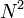 .
. - התמרת פורייה המהירה (FFT) מבצעת את אותו חישוב בכמות פעולות בסדר גודל של
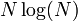 .
.
משמעות ההתמרה
- תהי פונקציה f. נדגום ממנה
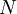 נקודות בתדר
נקודות בתדר 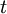 , כלומר נתון לנו:
, כלומר נתון לנו:
- נסמן נקודות אלה ב
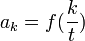
- אנו רוצים לפרק אותה לסכום של גלים:
- כיוון שהתדר של
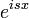 הוא
הוא 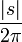 נובע כי הגלים הללו הם בתדרים
נובע כי הגלים הללו הם בתדרים 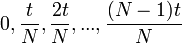
- שימו לב - ככל שנדגום יותר נקודות נקבל יותר מגוון של תדרים. מצד שני, נביט בחלון זמן יותר ארוך ונפספס שינויי תדרים מהירים יותר.
- נוכיח שפירוק זה תמיד אפשרי כך שיהיה שיוויון בכל נקודות הדגימה, ונקשר בין סדרת המקדמים להתמרת הפורייה של נקודות הדגימה.
- נביט בפונקצית הגל
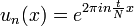 .
. - נציב בה את נקודות הדגימה ונקבל את הוקטור המרוכב:
- נציב בפונקציה הנתונה f את נקודות הדגימה ונקבל את הוקטור המרוכב:
- לכן אנו מעוניינים בפתרון למשוואה:
- זה בדיוק אומר שהפירוק של הפונקציה לגלים מתקיים בכל נקודות הדגימה:
- נבחן את הקבוצה
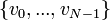 .
.
- עבור
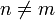 :
:
- אבל זה בדיוק סכום סדרה הנדסית
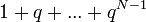 עבור
עבור 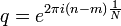
- שימו לב ש
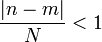 ולכן
ולכן 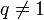 .
. - כמו כן, שימו לב ש
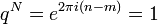
- לכן לפי הנוסחא לסכום סדרה הנדסית נקבל כי:
- כלומר גילינו כי
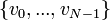 קבוצה אורתוגונלית (לא אורתונורמלית) ומהווה בסיס.
קבוצה אורתוגונלית (לא אורתונורמלית) ומהווה בסיס. - לכן ניתן בקלות לחשב את המקדמים
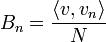
- לבסוף, נשים לב כי:
- כלומר
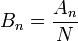
התמרת פורייה הבדידה ההפוכה
- מכאן גם ניתן להסיק ישירות את התמרת פורייה ההפוכה, שמחזירה את סדרת המקדמים
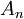 לסדרת הדגימות
לסדרת הדגימות 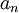 .
.
- ולכן:
מסקנות לגבי גלים ממשיים
- פירקנו את הפונקציה לסכום של גלים מרוכבים בנקודות הדגימה, האם ניתן להשתמש בהתמרה על מנת לקבל פירוק לגלים ממשיים?
- ראשית, נשים לב לתופעה הבאה:
- (השיוויון נכון בזכות המחזוריות)
- ולכן נקבל:
- כלומר פירוק הפונקציה לגלים
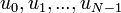 נותן את אותם המקדמים כמו פירוק הפונקציה לגלים
נותן את אותם המקדמים כמו פירוק הפונקציה לגלים 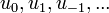 .
. - כאשר המקדם של
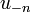 שווה למקדם של
שווה למקדם של 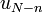 .
. - שימו לב שזה לא פירוק של הפונקציה לסכום הגלים בכל הממשיים, אלא רק בנקודות הדגימה.
- לדוגמא:
- נניח שיש לנו 5 דגימות של f.
- אם נפרק את f לגלים
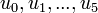 נקבל
נקבל 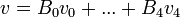
- אם נפרק את f לגלים
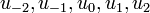 נקבל
נקבל 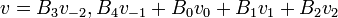
- במצב זה, אם דגמנו בתדר
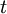 נקבל את התדרים
נקבל את התדרים  שזה מתאים למשפט הדגימה של שנון (טווח התדרים של הפונקציה הוא עד חצי מתדר הדגימה).
שזה מתאים למשפט הדגימה של שנון (טווח התדרים של הפונקציה הוא עד חצי מתדר הדגימה).
- עבור n ספציפי מתקיים כי:
- מהצבה ישירה של הנוסחאות שמצאנו ניתן לראות שאם f ממשית אזי
 וגם
וגם 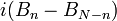 הם ממשיים.
הם ממשיים. - כלומר הצלחנו לפרק את f לסכום של גלים ממשיים עם מקדמים ממשיים.
- הערה: אם N זוגי, אז הגל
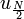 נותר בודד.
נותר בודד. - לדוגמא עבור
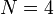 נקבל במקום הגלים
נקבל במקום הגלים 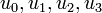 את
את 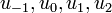
- נשים לב כי במקרה זה
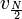 הוא וקטור ממשי (ולכן גם המקדם שלו ממשי) כיוון שהsin מתאפס בכל נקודות הדגימה.
הוא וקטור ממשי (ולכן גם המקדם שלו ממשי) כיוון שהsin מתאפס בכל נקודות הדגימה.
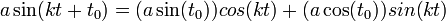
![\sin(a)\sin(b)=\frac{1}{2}\left[\cos(a-b)-\cos(a+b)\right]](/images/math/2/5/f/25f8d4d6c77a138100c89a987596ad1a.png)
![\cos(a)\cos(b)=\frac{1}{2}\left[\cos(a+b)+\cos(a-b)\right]](/images/math/f/4/9/f49ffa386014bd9ab57625ca1919dc7d.png)
![\frac{1}{\pi}\int_{-\pi}^{\pi}\sin(nx)\sin(nx)dx = \frac{1}{2\pi}\int_{-\pi}^{\pi}(1-\cos(2nx))dx = \frac{1}{2\pi}\left[x-\frac{1}{2n}\sin(2nx)\right]_{-\pi}^{\pi}=1](/images/math/7/9/b/79b96630be4b13a139e89a28e5c3417b.png)
![\frac{1}{\pi}\int_{-\pi}^{\pi}\cos(nx)\cos(nx)dx = \frac{1}{2\pi}\int_{-\pi}^{\pi}(\cos(2nx)+1)dx = \frac{1}{2\pi}\left[\frac{1}{2n}\sin(2nx)+x\right]_{-\pi}^{\pi}=1](/images/math/2/7/b/27bf3f269b2c1bad9a888e32febb6afb.png)
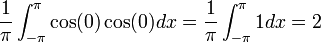
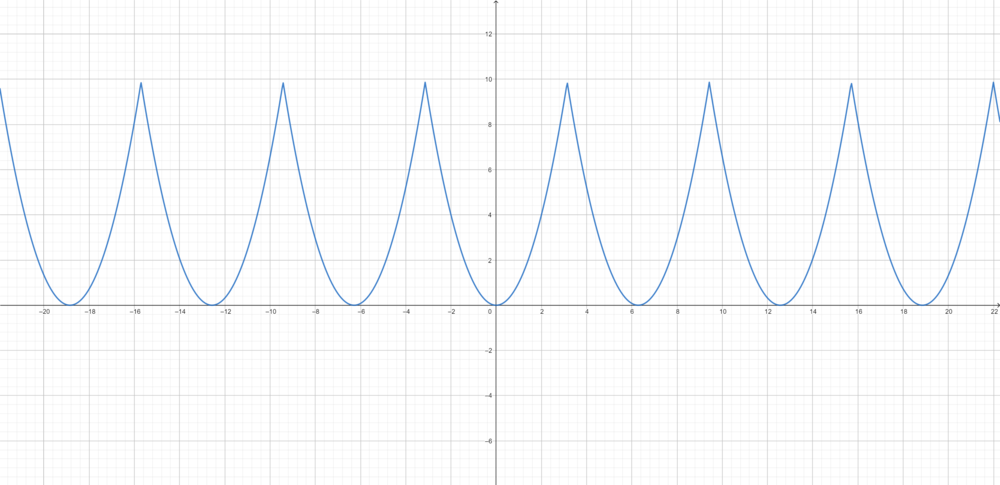
![a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}x^2dx =\frac{2}{\pi}\int_{0}^{\pi}x^2dx= \frac{2}{\pi}\left[\frac{1}{3}x^3\right]_{0}^{\pi} = \frac{2\pi^2}{3}](/images/math/6/6/f/66f8ca0042ee471a64c81bf7579cf761.png)
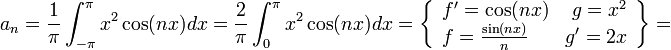
![=\frac{2}{\pi}\left[\frac{x^2\sin(nx)}{n}\right]_0^{\pi} - \frac{4}{n\pi}\int_{0}^{\pi}x\sin(nx)dx = - \frac{4}{n\pi}\int_{0}^{\pi}x\sin(nx)dx=
\left\{\begin{array}{lr}f'=\sin(nx) & g=x\\ f= -\frac{\cos(nx)}{n} & g'=1\end{array}\right\}=](/images/math/5/1/5/515fbb2ba109a06847f638fe4e5c9362.png)
![- \frac{4}{n\pi}\left[\frac{-x\cos(nx)}{n}\right]_0^\pi + \frac{4}{n^2\pi}\int_0^\pi \cos(nx)dx=\frac{4\pi\cos(\pi n)}{n^2\pi}+\frac{4}{n^3\pi}\left[sin(nx)\right]_0^\pi = \frac{4(-1)^n}{n^2}](/images/math/9/6/2/9628cd82e657ebc65624a51d3a39dcb9.png)
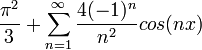
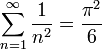
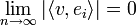
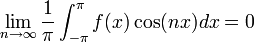
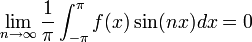
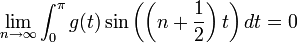
![\int_0^\pi \cos(kt)dt = \left[\frac{\sin(kt)}{k}\right]_0^\pi = 0](/images/math/c/e/c/ceca17ddf194fb7529f19b1be4606a29.png)
![\frac{1}{\pi}\int_0^\pi D_n(t)dt = \frac{1}{\pi}\int_0^\pi \left[\frac{1}{2} + \cos(t) + \cos(2t)+...+\cos(nt)\right]dt = \frac{1}{\pi}\int_0^\pi \frac{1}{2}dt = \frac{1}{2}](/images/math/d/e/4/de4fc431e4665baa4968ff0b9dc3ad7b.png)
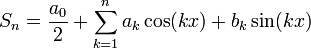
![S_n = \frac{1}{\pi}\int_{-\pi}^\pi \frac{1}{2}f(t)dt + \sum_{k=1}^n \left[\frac{1}{\pi}\int_{-\pi}^\pi f(t)\cos(kt)dt\right]\cos(kx)+\left[\frac{1}{\pi}\int_{-\pi}^\pi f(t)\sin(kt)dt\right]\sin(kx)=](/images/math/9/5/3/95388d9b466e3dbd694aa9869a5afd44.png)
![= \frac{1}{\pi}\int_{-\pi}^\pi\left[\frac{1}{2}f(t)+\sum_{k=1}^n f(t)\left(\cos(kt)\cos(kx) + \sin(kt)\sin(kx)\right)\right]dt=](/images/math/e/a/b/eabf1736c44842010763f0329c0ffc26.png)
![=\frac{1}{\pi}\int_{-\pi}^\pi f(t)\left[\frac{1}{2}+\sum_{k=1}^n \cos(k(t-x))\right]dt](/images/math/a/a/6/aa6a06b8a5efdbd5d653eaadfefaf68a.png)
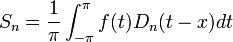
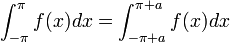
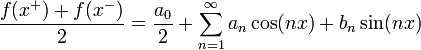
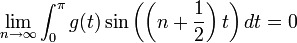
![0=\lim_{n\to\infty}\frac{1}{\pi}\int_0^\pi \left[f(x+t)-f(x^+)\right]\frac{\sin\left(\left(n+\frac{1}{2}\right)t\right)}{2\sin(\frac{t}{2})}dt=
\lim_{n\to\infty}\frac{1}{\pi}\int_0^\pi \left[f(x+t)-f(x^+)\right]D_n(t)dt](/images/math/2/5/0/25079825d14e4fc51335965cdd7ecfdc.png)
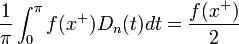
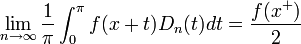
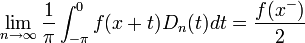
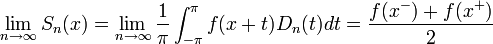
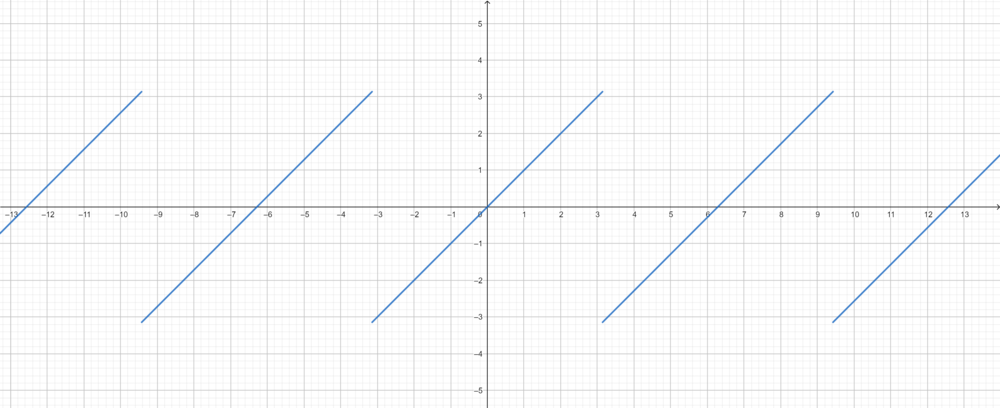
![b_n=\langle f,sin(nx)\rangle = \frac{1}{\pi}\int_{-\pi}^\pi x\sin(nx)dx =\frac{2}{\pi}\int_{0}^\pi x\sin(nx)dx= \frac{2}{n\pi}\left[-x\cos(nx)\right]_{0}^\pi + \frac{2}{n\pi}\int_{0}^{\pi}\cos(nx)dx =
-\frac{2\pi\cos(\pi n)}{\pi n} = \frac{2(-1)^{n+1}}{n}](/images/math/6/6/7/667a71b4b89b6be1016ffe8685a05701.png)
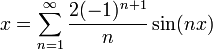
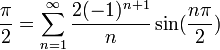
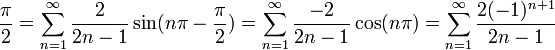
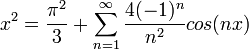
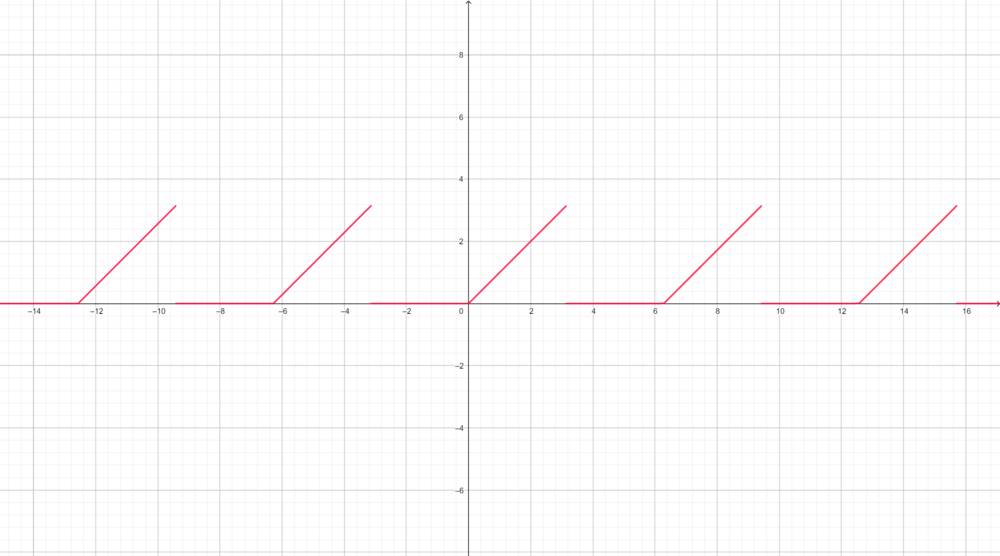
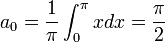
![a_n = \frac{1}{\pi}\int_0^\pi x\cos(nx)dx = \frac{1}{n\pi}\left[x\sin(nx)\right]_0^\pi - \frac{1}{n\pi}\int_0^\pi \sin(nx)dx = \frac{1}{n^2\pi}\left[\cos(nx)\right]_0^\pi=
\frac{(-1)^n-1}{\pi n^2}](/images/math/f/9/c/f9c400eb7eee75c918584f6338d9afa0.png)
![b_n = \frac{1}{\pi}\int_0^\pi x\sin(nx)dx = \frac{-1}{n\pi}\left[x\cos(nx)\right]_0^\pi + \frac{1}{n\pi}\int_0^\pi \cos(nx)dx = \frac{(-1)^{n+1}}{n}](/images/math/4/8/1/481014b617b9eec391447cfa2a17f5f3.png)
![h(x) = \frac{\pi}{4} + \sum_{n=1}^\infty \left[\frac{(-1)^n-1}{\pi n^2}\cos(nx) + \frac{(-1)^{n+1}}{n}\sin(nx)\right]](/images/math/1/4/3/143130c2a183c3e0b99dd1d856502de9.png)
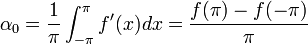
![\alpha_n=\frac{1}{\pi} \int_{-\pi}^\pi f'(x)\cos(nx)dx = \frac{1}{\pi}\left[f(x)\cos(nx)\right]_{-\pi}^\pi +\frac{n}{\pi}\int_{-\pi}^\pi f(x)\sin(nx)dx =
\frac{(-1)^n\left(f(\pi)-f(-\pi)\right)}{\pi}+n\cdot b_n = (-1)^n\alpha_0+nb_n](/images/math/e/9/b/e9b5cde5f0ea97cd0e133da365d76f3a.png)
![\beta_n=\frac{1}{\pi} \int_{-\pi}^\pi f'(x)\sin(nx)dx = \frac{1}{\pi}\left[f(x)\sin(nx)\right]_{-\pi}^\pi -\frac{n}{\pi}\int_{-\pi}^\pi f(x)\cos(nx)dx = -n\cdot a_n](/images/math/f/4/1/f4193cb204160349b34349a553bbc996.png)
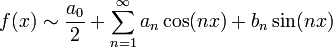
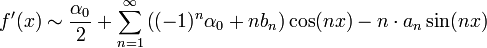
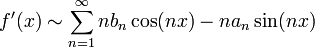
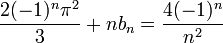
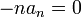
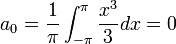
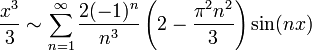
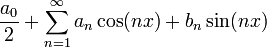
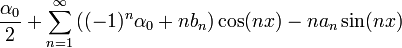

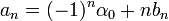
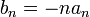
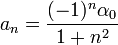
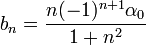
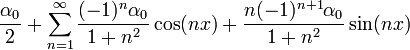
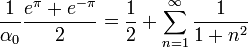
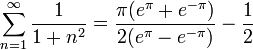
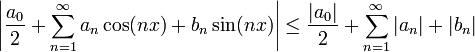
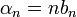
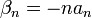
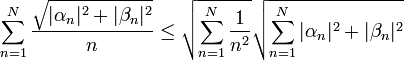
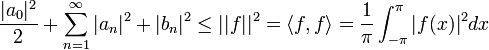
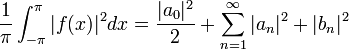
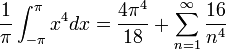
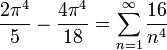
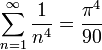
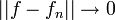
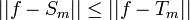
![\int_{-\pi}^{\pi} |f-g|^2dx \leq \sum_{k=1}^n \sup_{[x_{k-1},x_k]}|f(x)-f(c_k)|^2 (x_k-x_{k-1}) \leq \sum_{k=1}^n \frac{\varepsilon}{2\pi}(x_k-x_{k-1}) = \varepsilon](/images/math/a/f/7/af73d143b413b49b353d05dfd359e577.png)
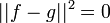
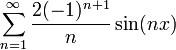
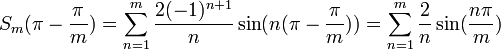
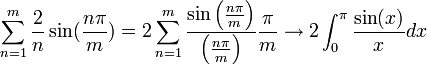
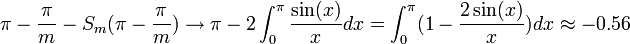
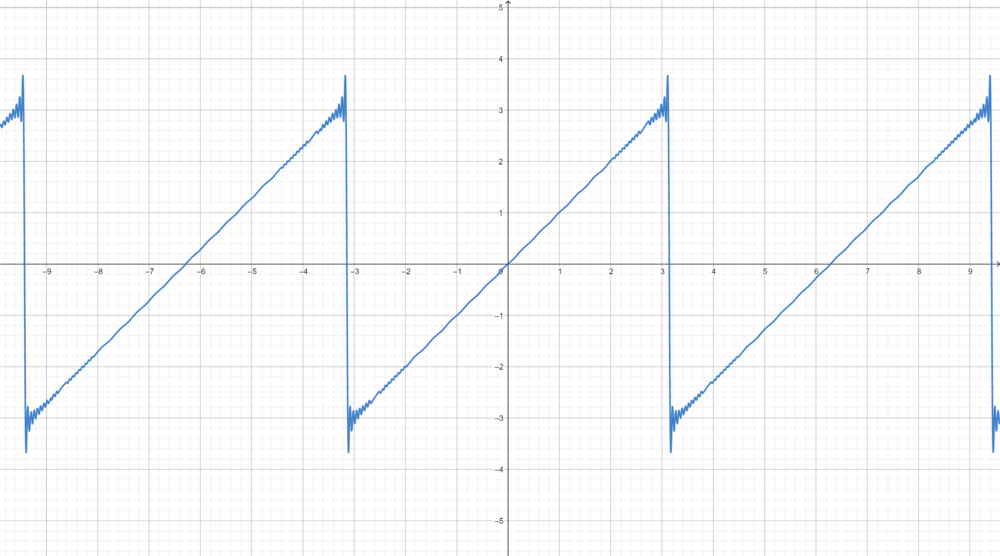
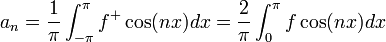
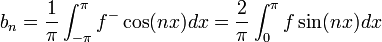
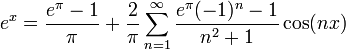
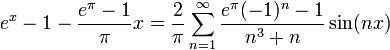
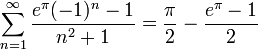
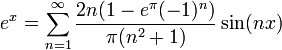
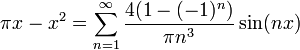
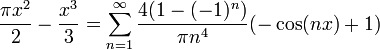
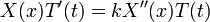
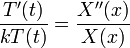
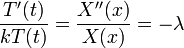
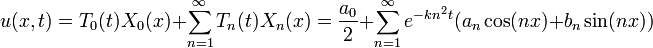
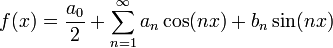
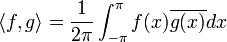
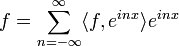
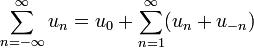
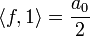
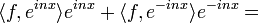
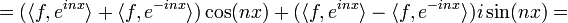
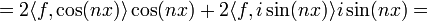
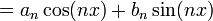
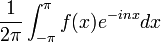
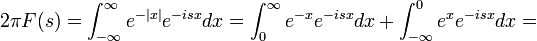
![=\left[\frac{e^{-x(1+is)}}{-(1+is)}\right]_0^\infty + \left[\frac{e^{x(1-is)}}{1-is}\right]_{-\infty}^0=\frac{1}{1+is} + \frac{1}{1-is} = \frac{2}{1+s^2}](/images/math/a/e/5/ae5cf9d26973f0db781d48222f6a06a2.png)
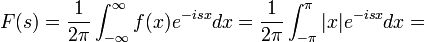
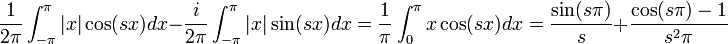
 = \frac{e^{\frac{-is}{2}}}{2\pi (1+(-\frac{s}{2})^2)}](/images/math/1/d/0/1d088157c02693fb0d8ed7acf23d50e6.png)
](/images/math/9/4/f/94f761ab6ed3959278149ee9498e3b78.png)
 = e^{-x^2}](/images/math/0/1/2/012f31ff7bdd71a87495157ce567474e.png)
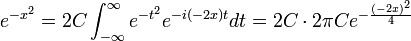
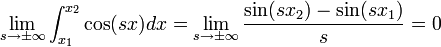
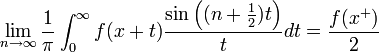
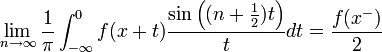
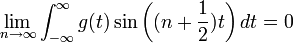
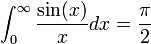
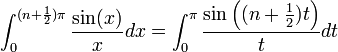
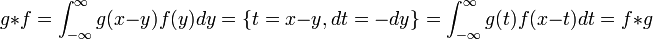
![\mathcal{F}[f*g] = \frac{1}{2\pi}\int_{-\infty}^\infty \left[\int_{-\infty}^\infty f(x-y)g(y)dy\right]e^{-isx}dx =](/images/math/e/3/b/e3bf2359cf80fa22ef87940b76bab395.png)
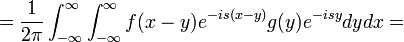
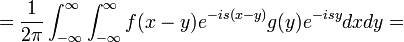
![= \frac{1}{2\pi}\int_{-\infty}^\infty \left[\int_{-\infty}^\infty f(x-y)e^{-is(x-y)}dx\right] g(y)e^{-isy}dy =](/images/math/e/b/d/ebd28639faadbb48d521782b07bb59f3.png)
![= \frac{1}{2\pi}\int_{-\infty}^\infty \left[\int_{-\infty}^\infty f(t)e^{-ist}dt\right] g(y)e^{-isy}dy =](/images/math/4/e/c/4ec78a9e304a8789998ec3268afca7aa.png)
![= 2\pi\left(\frac{1}{2\pi}\int_{-\infty}^\infty f(t)e^{-ist}dt\right) \cdot \left( \frac{1}{2\pi}\int_{-\infty}^\infty g(y)e^{-isy}dy\right) =2\pi \cdot \mathcal{F}[f] \cdot \mathcal{F}[g]](/images/math/b/a/e/baeb68621f9214e25738e375196c71b7.png)
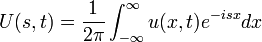
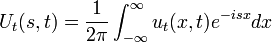
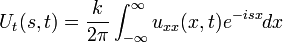
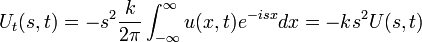
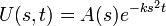
![A(s) = U(s,0) = \frac{1}{2\pi}\int_{-\infty}^{\infty} u(x,0)e^{-isx}dx = \frac{1}{2\pi}\int_{-\infty}^{\infty} f(x)e^{-isx}dx = \mathcal{F}[f]](/images/math/b/2/3/b23f76ed67da76ade8e48dd94000a40a.png)
![\mathcal{F}^{-1}[e^{-ks^2 t}]=\int_{-\infty}^\infty e^{-ks^2 t}e^{isx}ds = \{s=\frac{u}{2\sqrt{kt}}\}=](/images/math/c/f/f/cffe5667792200049832f52d0b65ebfc.png)
 = \frac{\sqrt{\pi}}{\sqrt{kt}}e^{-\frac{x^2}{4kt}}](/images/math/9/f/f/9ff1fd9032852f317c879032f37075ce.png)
![\mathcal{F}[u] = \mathcal{F}[f]\cdot \mathcal{F}[p]](/images/math/6/6/c/66c99baee865090e05d9f47c874db097.png)
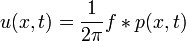
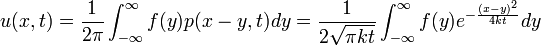
e^{isx}ds = \int_{-2\pi t}^{2\pi t}\mathcal{F}[f](s)e^{isx}ds](/images/math/a/f/b/afbed5250016cc979bbc2aa86f9f73b2.png)
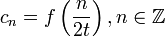
e^{is\left(\frac{n}{2t}\right)}ds](/images/math/4/f/d/4fd43aac3143dcc70c7d69ea6ebad0e4.png)
e^{-inx}dx](/images/math/f/4/8/f48acec86e568848279ffd68a14d2324.png)