הבדלים בין גרסאות בדף "88-201 תשעו סמסטר ב"
(←בוחן) |
(←תרגילים) |
||
| שורה 62: | שורה 62: | ||
תרגיל 5 עוסק בעקמומיות של עקומות מישוריות ובתבנית היסודית הראשונה של משטחים. | תרגיל 5 עוסק בעקמומיות של עקומות מישוריות ובתבנית היסודית הראשונה של משטחים. | ||
| + | |||
| + | [[מדיה:תרגיל_6_גיאומטריה_תשעו.pdf | תרגיל 6]] | ||
| + | |||
| + | [[מדיה:פתרון_תרגיל_6_גיאומטריה_תשעו.pdf | פתרון תרגיל 6]] | ||
| + | |||
| + | תרגיל 6 עוסק בתבנית היסודית הראשונה ובשימושים שלה. | ||
==בוחן== | ==בוחן== | ||
גרסה מ־07:26, 13 באפריל 2016
88-201 גיאומטריה אנליטית ודיפרנציאלית
תוכן עניינים
חומר עזר
- סיכומי הרצאות ותרגולים של עידן אריה
- סיכומי הרצאות 2011 (פרופ' כץ)
- חוברת הקורס של פרופ' כץ (באנגלית)
- דף נוסחאות
- מבחנים ופתרונות משנים קודמות
- חוברת תרגילים (באנגלית)
- שאלות לדוגמה
- פתרונות לשאלות
- משטחים ריבועיים ומשוואותיהם
- חתכי חרוט
הודעות
ברוכים הבאים וברוכות הבאות לקורס גיאומטריה אנליטית ודיפרנציאלית. יהיה בסדר, מבטיח.
שעת קבלה
שעת הקבלה היא ביום שני ב12, בתיאום מראש במייל.
שינוי כיתה
התרגול מתקיים בבניין 507 כיתה 202.
תרגילים
התרגילים לא להגשה, והם עולים ביחד עם הפתרונות. חשוב שתנסו לפתור אותם ותוודאו שהפתרונות מובנים.
תרגיל 1 עוסק בסכימת איינשטיין.
בשורה האחרונה, האינדקס העליון באיבר הראשון משמאל הוא i ולא j. תודה לבר על התיקון.
תרגיל 2 עוסק במכפלה הסקלרית, במכפלה הוקטורית ובתבניות ריבועיות במישור.
תרגיל 3 עוסק בתבניות ריבועיות במרחב, במטריצות סיבוב ובסיווג נקודות קריטיות של פונקציות מהמישור לישר הממשי.
בתרגיל ביקשתי לסובב ב-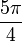 ובפתרון סובבתי ב-
ובפתרון סובבתי ב-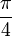 ; הדברים בכל אופן מאד פשוטים.
; הדברים בכל אופן מאד פשוטים.
תרגיל 4 עוסק באורך עקומה, פרמטריזציה טבעית ועקמומיות של עקומות מישוריות.
תרגיל 5 עוסק בעקמומיות של עקומות מישוריות ובתבנית היסודית הראשונה של משטחים.
תרגיל 6 עוסק בתבנית היסודית הראשונה ובשימושים שלה.
בוחן
הבוחן ייערך ב-19.05 י"א אייר. תקבלו הודעה על שעה ומיקום.
החומר לבוחן הוא כל מה שנלמד עד פסח.
השאלות בבוחן יילקחו מחוברת התרגולים.
בבוחן תהיינה 3 שאלות ובונוס.
תרגולים מסמסטר קיץ תשע"ה (של אלעד עטייא)
מצאת טעות? אשמח לשמוע - atian@walla.com. מלשמוע ועד אשכרה לתקן יש, כמובן, מרחק לא קטן.
איור להמחשת השאלה על פרמטריזציה של המעגל באמצעות המרחק בין החיתוך בין המיתר וציר ה-y לבין הראשית
כדי לראות איור מדויק מתמטית של הקפיץ, חפשו Helicoid בגוגל.