הבדלים בין גרסאות בדף "83-110 לינארית להנדסה תשעח סמסטר א"
מתוך Math-Wiki
1593237070 (שיחה | תרומות) |
|||
| (35 גרסאות ביניים של 5 משתמשים אינן מוצגות) | |||
| שורה 5: | שורה 5: | ||
מרצה: ד"ר מיטל | מרצה: ד"ר מיטל | ||
| − | מתרגלים: אחיה, | + | מתרגלים: אחיה, אריאל, עדי ועוזי |
==קישורים== | ==קישורים== | ||
| שורה 12: | שורה 12: | ||
*[[83-110 לינארית להנדסה תשעד סמסטר א/מערכי תרגול|מערכי תרגול]] | *[[83-110 לינארית להנדסה תשעד סמסטר א/מערכי תרגול|מערכי תרגול]] | ||
| − | *[[83-110 לינארית להנדסה תשעד סמסטר א/תרגילים|תרגילים משנים קודמות - לא להגשה(לתירגול נוסף)]] | + | *[[83-110 לינארית להנדסה תשעד סמסטר א/תרגילים|תרגילים משנים קודמות, תשע"ד - לא להגשה(לתירגול נוסף)]] |
| + | *[[83-110 לינארית להנדסה תשעז סמסטר ב|תרגילים משנים קודמות, תשע"ז סמסטר ב - לא להגשה(לתירגול נוסף)]] | ||
| + | *[[83-110 תרגילים תיאורטיים|תרגילים משנים קודמות, תשע"ז סמסטר א - לא להגשה(לתירגול נוסף)]] | ||
*[[88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 3.5|אינדוקציה]] | *[[88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 3.5|אינדוקציה]] | ||
| שורה 22: | שורה 24: | ||
*[[83-110 בחנים בלינארית להנדסה |בחנים משנים קודמות]] | *[[83-110 בחנים בלינארית להנדסה |בחנים משנים קודמות]] | ||
| + | * [[מדיה: svd.pdf|דוגמה לפירוק SVD]] + תוספת לגבי מציאת U בדרך השניה : [[מדיה: svd2.pdf|מציאת U בפירוק SVD]] | ||
| + | * [https://toodle2.cs.huji.ac.il/nu14/pluginfile.php/252154/mod_resource/content/4/Linear_Alg_2_2015_TA12.pdf עיבוד תמונה וSVD] | ||
| + | *תרגילים בפירוק SVD ניתן למצוא בקורס שלנו 83110 שנת תשע"ג תרגיל 12. | ||
==הודעות== | ==הודעות== | ||
| + | *לקבוצה של אריאל (כולם מוזמנים להציץ) - בקישור [[תרגיל על קבוצה פורשת]] תוכלו לראות את הפיתרון לתרגיל שלא סיימנו. | ||
| + | |||
| + | *המשפטים למבחן : משפט השלישי חינם, ע"ע : ריבוי אלגברי >= ריבוי גיאוטרי, משפט המימדים של העתקה לינארית. בנוסף - תרגיל 9 : שאלה 10, תרגיל 12 : שאלות 1,2,5. | ||
==תרגילי בית == | ==תרגילי בית == | ||
'''מטלות תרגול ממוחשבות XI:''' [http://xi.math-wiki.com בקישור]. בכל שבוע יתפרסם תרגיל. | '''מטלות תרגול ממוחשבות XI:''' [http://xi.math-wiki.com בקישור]. בכל שבוע יתפרסם תרגיל. | ||
הסדר הוא: שבוע תרגיל XI, שבוע תרגיל XI, שבוע תרגיל ידני, וכך שוב ושוב ושוב :) | הסדר הוא: שבוע תרגיל XI, שבוע תרגיל XI, שבוע תרגיל ידני, וכך שוב ושוב ושוב :) | ||
| + | |||
| + | *[[מדיה:Ex3LAE18.pdf|תרגיל 3]], [[מדיה:Sol3LAE18.pdf|פתרון תרגיל 3]] | ||
| + | *תרגיל 4 - XI, עד ז' כסלו (25.11) כולל. | ||
| + | *תרגיל 5 - XI, עד י"ב כסלו (30.11) כולל. | ||
| + | *[[מדיה:Ex6LAE18.pdf|תרגיל 6]], [[מדיה:Sol6LAE18.pdf|פתרון תרגיל 6]] הארכת הגשה: בתרגול בשבוע שמתחיל בכ"ב כסלו, 10.12 | ||
| + | *תרגיל 7 - XI עד 17.12. | ||
| + | *תרגיל 8 - XI.עד 24.12. | ||
| + | *[[מדיה:Ex9LAE18a.pdf|תרגיל 9]], [[מדיה:Sol9LAE18.pdf|פתרון תרגיל 9]] הגשה: בתרגול בשבוע שמתחיל ב-י"ג טבת, 31.12 | ||
| + | *תרגיל 10 - XI.עד 7.1. | ||
| + | *תרגיל 11 - XI.עד 14.1. | ||
| + | *[[מדיה:Ex12LAE18a.pdf|תרגיל 12]], [[מדיה:Sol12LAE18.pdf|פתרון תרגיל 12]] הגשה: עד לתירגול האחרון. ללא דחיות. התחילו לפתור את השאלות שאתם יכולים. | ||
| + | === רמזים יותר עבים לתרגיל 12=== | ||
| + | *שאלה 1: ראינו כי <math>C(A)=\left\{ Ax:\,x\in\mathbb{R}^{3}\right\} </math> ולכן השאלה היא בעצם למצוא <math>b'\in C(A)</math> ש"הכי קרוב" ל b (במובן של <math>\Vert b-b'\Vert</math> מינמאלי). זה בדיוק התכונה של ההטלה <math>\pi_{C(A)}(b)</math> | ||
| + | *שאלה 2: נעבוד עם נורמה בריבוע בכל מקום. מחישוב ישיר מקבלים כי <math>\Vert v-u\Vert^{2}=\Vert v\Vert^{2}-2Re(\left\langle v,u\right\rangle )+1</math> לכל <math>u\in S</math>. חשבו בצורה דומה גם את <math>\Vert v-\frac{v}{\Vert v\Vert}\Vert^{2}</math> והראו כי הוא יותר קטן (בעזרת קושי שוורץ). | ||
| + | *שאלה 3: סעיף א -נסו תחילה להבין מה קורה ב k=2. סעיף ב- זה הכללה של סעיף א | ||
| + | *שאלה 4: נעזרת בשאלה 3 | ||
==בוחן== | ==בוחן== | ||
| + | * תאריך: 11.12.2017 (11 בדצמבר 2017), בשעות מחלקה. | ||
| + | * זמן: הבוחן יהיה שעה ועשרים! | ||
| + | * חומר: מתחילת הקורס עד מרחבים וקטורים ותתי מרחבים וקטורים (כולל). באופן שקול: עד תלות ופרישה לא כולל. | ||
| + | * פרטים נוספים בהמשך | ||
| + | * [https://docs.google.com/spreadsheets/d/e/2PACX-1vQUcKCcJ7-SwYGOFsnjTRDfE9Yq_qzD84wNiEkXoGxxe6Pmq-bex-eZb1slkt6xVxsG14OeHHV4qnfU/pubhtml?gid=877849890&single=true ציונים] | ||
| + | |||
| + | ==ציוני תרגיל== | ||
| + | *ציוני התרגיל מפורסמים [https://docs.google.com/spreadsheets/d/e/2PACX-1vQ-HKWYx3sXvIAtjJaLgrLlb3pZLnkj89M-7gCwFte51uW6rsOF500-__r_79r3fpnai9zHLZAS0wFk/pubhtml?gid=768705969&single=true כאן]. | ||
| + | *ציון התרגיל מורכב משלושה ציוני ביניים שהם: ממוצע 7 התרגילים הטובים ב-Xi, ממוצע 3 התרגילים הטובים הידניים והבוחן. | ||
| + | חישוב הציון הסופי בוצע בעזרת הנוסחא <math>0.6*Max\left\{Max\left\{Theoretical,Quiz\right\},Xi\right\}+0.4*Min\left\{Max\left\{Theoretical,Quiz\right\},Xi\right\}</math> | ||
| + | *אם יש שאלות בנוגע לציון התרגיל פנו למתרגלים עוד השבוע כי שבוע הבא (25.2) הציונים יגשו. | ||
גרסה אחרונה מ־10:57, 20 בפברואר 2018
סגל הקורס:
מרצה: ד"ר מיטל
מתרגלים: אחיה, אריאל, עדי ועוזי
קישורים
- תרגילים משנים קודמות, תשע"ד - לא להגשה(לתירגול נוסף)
- תרגילים משנים קודמות, תשע"ז סמסטר ב - לא להגשה(לתירגול נוסף)
- תרגילים משנים קודמות, תשע"ז סמסטר א - לא להגשה(לתירגול נוסף)
- דוגמה לפירוק SVD + תוספת לגבי מציאת U בדרך השניה : מציאת U בפירוק SVD
- תרגילים בפירוק SVD ניתן למצוא בקורס שלנו 83110 שנת תשע"ג תרגיל 12.
הודעות
- לקבוצה של אריאל (כולם מוזמנים להציץ) - בקישור תרגיל על קבוצה פורשת תוכלו לראות את הפיתרון לתרגיל שלא סיימנו.
- המשפטים למבחן : משפט השלישי חינם, ע"ע : ריבוי אלגברי >= ריבוי גיאוטרי, משפט המימדים של העתקה לינארית. בנוסף - תרגיל 9 : שאלה 10, תרגיל 12 : שאלות 1,2,5.
תרגילי בית
מטלות תרגול ממוחשבות XI: בקישור. בכל שבוע יתפרסם תרגיל. הסדר הוא: שבוע תרגיל XI, שבוע תרגיל XI, שבוע תרגיל ידני, וכך שוב ושוב ושוב :)
- תרגיל 3, פתרון תרגיל 3
- תרגיל 4 - XI, עד ז' כסלו (25.11) כולל.
- תרגיל 5 - XI, עד י"ב כסלו (30.11) כולל.
- תרגיל 6, פתרון תרגיל 6 הארכת הגשה: בתרגול בשבוע שמתחיל בכ"ב כסלו, 10.12
- תרגיל 7 - XI עד 17.12.
- תרגיל 8 - XI.עד 24.12.
- תרגיל 9, פתרון תרגיל 9 הגשה: בתרגול בשבוע שמתחיל ב-י"ג טבת, 31.12
- תרגיל 10 - XI.עד 7.1.
- תרגיל 11 - XI.עד 14.1.
- תרגיל 12, פתרון תרגיל 12 הגשה: עד לתירגול האחרון. ללא דחיות. התחילו לפתור את השאלות שאתם יכולים.
רמזים יותר עבים לתרגיל 12
- שאלה 1: ראינו כי
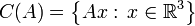ולכן השאלה היא בעצם למצוא 
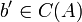ש"הכי קרוב" ל b (במובן של 
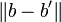מינמאלי). זה בדיוק התכונה של ההטלה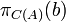 
- שאלה 2: נעבוד עם נורמה בריבוע בכל מקום. מחישוב ישיר מקבלים כי
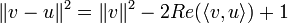לכל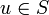 
. חשבו בצורה דומה גם את 
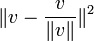והראו כי הוא יותר קטן (בעזרת קושי שוורץ). - שאלה 3: סעיף א -נסו תחילה להבין מה קורה ב k=2. סעיף ב- זה הכללה של סעיף א
- שאלה 4: נעזרת בשאלה 3
בוחן
- תאריך: 11.12.2017 (11 בדצמבר 2017), בשעות מחלקה.
- זמן: הבוחן יהיה שעה ועשרים!
- חומר: מתחילת הקורס עד מרחבים וקטורים ותתי מרחבים וקטורים (כולל). באופן שקול: עד תלות ופרישה לא כולל.
- פרטים נוספים בהמשך
- ציונים
ציוני תרגיל
- ציוני התרגיל מפורסמים כאן.
- ציון התרגיל מורכב משלושה ציוני ביניים שהם: ממוצע 7 התרגילים הטובים ב-Xi, ממוצע 3 התרגילים הטובים הידניים והבוחן.
חישוב הציון הסופי בוצע בעזרת הנוסחא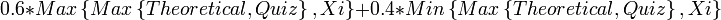 
- אם יש שאלות בנוגע לציון התרגיל פנו למתרגלים עוד השבוע כי שבוע הבא (25.2) הציונים יגשו.
