הבדלים בין גרסאות בדף "89-214 תשף סמסטר א"
(←תרגילי בית) |
(←לא מדויק) |
||
| (25 גרסאות ביניים של 5 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| + | |||
'''[[89-214 מבנים אלגבריים]]''' | '''[[89-214 מבנים אלגבריים]]''' | ||
| שורה 7: | שורה 8: | ||
* [http://abstract.ups.edu/aata/ Abstarct Algebra - Theory and Applications ] מאת Thomas W. Judson. | * [http://abstract.ups.edu/aata/ Abstarct Algebra - Theory and Applications ] מאת Thomas W. Judson. | ||
* [https://www.shoup.net/ntb A Computational Introduction to Number Theory and Algebra] מאת Victor Shoup. | * [https://www.shoup.net/ntb A Computational Introduction to Number Theory and Algebra] מאת Victor Shoup. | ||
| + | * [[מדיה:19CSASnotes.pdf|סיכום ההרצאות מ2019 ע"י ספיר ביתן]] | ||
==הודעות== | ==הודעות== | ||
| + | |||
| + | ===הרצאת העשרה=== | ||
| + | ביום רביעי הקרוב 25.12.2019 בשעה 14:30 מתוכננת הרצאת העשרה (שאינה חובה) שהנושא שלה הוא היכרות עם [https://www.sagemath.org SageMath] ושימושים לתורת החבורות. ההרצאה תתקיים בבניין 507 בחדר 101. | ||
| + | |||
| + | ===רמזים לתרגיל בית 7=== | ||
| + | |||
| + | בסעיף 4ד' אפשר להתחיל במציאת שיכון של <math>A_4</math> ב-<math>S_5</math> ללא שום הגבלות. זה די קל, והעתקת הזהות היא כיוון התחלתי די טוב, כשצריך לדאוג לאן <math>5</math> נשלח בתמורות של <math>S_5</math>. אחר כך כדאי לנסות למצוא שיכון של <math>A_4</math> ב-<math>S_5</math> רק עם המגבלה שבה <math>(1,2,3)\in A_4</math> לא נשלח ל-<math>(1,2,3)\in S_5</math>. האם יש עותק אחר של <math>S_4</math> בתוך <math>S_5</math> חוץ מזה שמצאתם בהתחלה? זה אמור לתת את הכיוון איך למצוא שיכון שמקיים את שתי ההגבלות שמופיעות בשאלה. | ||
| + | |||
| + | בסעיף 4ה' כדאי לנסות בהתחלה לשכן את <math>\mathbb{Z}_n</math> ב-<math>S_{7ab}</math>. אם במקרה <math>a=b=0</math>, איך תשכנו את <math>\mathbb{Z}_3</math> ב-<math>S_{700}</math>? לאן ישלח כל איבר של <math>\mathbb{Z}_3</math> אחרי שנדע שהאיבר <math>1\in\mathbb{Z}_3</math> נשלח לתמורה <math>\sigma\in S_{700}</math>? רק קצת יותר קשה לשכן עכשיו את <math>\mathbb{Z}_{1000}</math> ב-<math>S_{700}</math>, כי אתם יודעים שאין מחזורים מאורך <math>1000</math> בחבורה <math>S_{700}</math>, אבל לפחות יש תמורות מסדר <math>1000</math>. עכשיו כדאי להזכר בזה שתמורות זרות (כאלו שהתומכים שלהן זרים) מתחלפות, ולמצוא שיכון של <math>\mathbb{Z}_3\times\mathbb{Z}_{1000}</math> ב-<math>S_{700}</math>. | ||
==תרגילי בית== | ==תרגילי בית== | ||
| שורה 18: | שורה 29: | ||
* [[מדיה: 89214exe1_2020A.pdf | תרגיל 1]], להגשה עד התאריך 13.11.2019. | * [[מדיה: 89214exe1_2020A.pdf | תרגיל 1]], להגשה עד התאריך 13.11.2019. | ||
* [[מדיה: 89214exe2_2020A.pdf | תרגיל 2]], להגשה עד התאריך 20.11.2019. | * [[מדיה: 89214exe2_2020A.pdf | תרגיל 2]], להגשה עד התאריך 20.11.2019. | ||
| + | * [[מדיה: 89214exe3_2020A.pdf | תרגיל 3]], להגשה עד התאריך 26.11.2019. | ||
| + | * [[מדיה: 89214exe4_2020A.pdf | תרגיל 4]], להגשה עד התאריך 4.12.2019. | ||
| + | * [[מדיה: 89214exe5_2020A.pdf | תרגיל 5]], להגשה עד התאריך 11.12.2019. | ||
| + | * [[מדיה: 89214exe6_2020A.pdf | תרגיל 6]], להגשה עד התאריך 18.12.2019. | ||
| + | * [[מדיה: 89214exe7_2020A.pdf | תרגיל 7]], להגשה עד התאריך 26.12.2019. | ||
| + | * [[מדיה: 89214exe8_2020A.pdf | תרגיל 8]], להגשה עד התאריך 8.1.2020. | ||
| + | * [[מדיה: 89214exe9_2020A.pdf | תרגיל 9]], להגשה עד התאריך 15.1.2020. | ||
| + | * [[מדיה: 89214exe10_2020A.pdf | תרגיל 10]], להגשה עד התאריך 28.1.2020. | ||
| + | ** צרפו את קבצי המקור שלכם. בדרך כלל אלו יהיו קבצים בסיומות כמו c, py, java או txt. בבקשה בלי צילומי מסך, צילום במצלמה של מסך, או [https://xkcd.com/763/ פתרונות יצירתיים] אחרים. | ||
| + | |||
| + | שאלות החימום הן שאלות שלא יקבלו ציון, והן בדרך כלל קלות יותר. אבל כדאי מאוד לוודא שיודעים איך לפתור אותן, אפילו בעל פה. | ||
| + | |||
| + | '''ציון התרגול''' יהיה הממוצע של הציונים של תרגילי הבית, אחרי שהוצאנו את שני התרגילים הנמוכים. | ||
| + | זה אומר שהציון לא יכול לרדת מהגשה של תרגיל, אלא רק להישאר או לעלות. | ||
==חוברת מערכי תרגול== | ==חוברת מערכי תרגול== | ||
| שורה 27: | שורה 52: | ||
==לא מדויק== | ==לא מדויק== | ||
| − | הבלוג [http://gadial.net/ לא מדויק] של גדי אלכסנדרוביץ' הוא מקור מצוין למי שחושב שאיבד את הדרך בקורס, וגם למי שלא. רוב הפוסטים שקשורים לקורס מופיעים ב[https://gadial.net/ | + | הבלוג [http://gadial.net/ לא מדויק] של גדי אלכסנדרוביץ' הוא מקור מצוין למי שחושב שאיבד את הדרך בקורס, וגם למי שלא. רוב הפוסטים שקשורים לקורס מופיעים ב[https://gadial.net/categories/abstract%20algebra/ קטגוריה אלגברה מופשטת], למשל: |
* [http://www.gadial.net/2017/02/01/group_definition/ אז מה זו בעצם חבורה?] | * [http://www.gadial.net/2017/02/01/group_definition/ אז מה זו בעצם חבורה?] | ||
גרסה אחרונה מ־07:36, 2 בספטמבר 2020
תוכן עניינים
קישורים
- מבחנים משנים קודמות
- תקצירי ההרצאות
- Abstarct Algebra - Theory and Applications מאת Thomas W. Judson.
- A Computational Introduction to Number Theory and Algebra מאת Victor Shoup.
- סיכום ההרצאות מ2019 ע"י ספיר ביתן
הודעות
הרצאת העשרה
ביום רביעי הקרוב 25.12.2019 בשעה 14:30 מתוכננת הרצאת העשרה (שאינה חובה) שהנושא שלה הוא היכרות עם SageMath ושימושים לתורת החבורות. ההרצאה תתקיים בבניין 507 בחדר 101.
רמזים לתרגיל בית 7
בסעיף 4ד' אפשר להתחיל במציאת שיכון של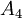 
ב-
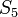ללא שום הגבלות. זה די קל, והעתקת הזהות היא כיוון התחלתי די טוב, כשצריך לדאוג לאן 
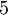נשלח בתמורות של 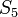. אחר כך כדאי לנסות למצוא שיכון של 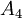ב-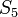 רק עם המגבלה שבה 
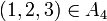לא נשלח ל-
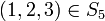. האם יש עותק אחר של 
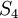בתוך 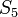חוץ מזה שמצאתם בהתחלה? זה אמור לתת את הכיוון איך למצוא שיכון שמקיים את שתי ההגבלות שמופיעות בשאלה.
בסעיף 4ה' כדאי לנסות בהתחלה לשכן את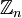 
ב-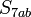
. אם במקרה 
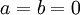, איך תשכנו את 
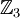ב-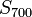
? לאן ישלח כל איבר של 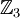אחרי שנדע שהאיבר 
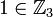נשלח לתמורה 
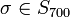? רק קצת יותר קשה לשכן עכשיו את 
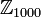ב-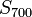, כי אתם יודעים שאין מחזורים מאורך 
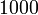בחבורה 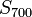, אבל לפחות יש תמורות מסדר 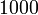. עכשיו כדאי להזכר בזה שתמורות זרות (כאלו שהתומכים שלהן זרים) מתחלפות, ולמצוא שיכון של 
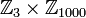ב-.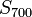
תרגילי בית
יש חובת הכנה לתרגילי הבית. יש להגיש את תרגילי הבית דרך מערכת הלמידה המתוקשבת https://lemida.biu.ac.il (המודל) בקבוצת ההרצאה אליה אתם רשומים. בעת ההגשה תצטרכו להעלות קובץ PDF (עדיף מוקלד) עם הפתרונות שלכם. מותר לעבוד יחד בקבוצות של עד שלושה סטודנטים, אך כל סטודנט צריך לכתוב את הפתרון שלו בעצמו ולהוסיף את שמות חברי הקבוצה בעמוד הראשון של הפתרון.
- תרגיל 1, להגשה עד התאריך 13.11.2019.
- תרגיל 2, להגשה עד התאריך 20.11.2019.
- תרגיל 3, להגשה עד התאריך 26.11.2019.
- תרגיל 4, להגשה עד התאריך 4.12.2019.
- תרגיל 5, להגשה עד התאריך 11.12.2019.
- תרגיל 6, להגשה עד התאריך 18.12.2019.
- תרגיל 7, להגשה עד התאריך 26.12.2019.
- תרגיל 8, להגשה עד התאריך 8.1.2020.
- תרגיל 9, להגשה עד התאריך 15.1.2020.
- תרגיל 10, להגשה עד התאריך 28.1.2020.
- צרפו את קבצי המקור שלכם. בדרך כלל אלו יהיו קבצים בסיומות כמו c, py, java או txt. בבקשה בלי צילומי מסך, צילום במצלמה של מסך, או פתרונות יצירתיים אחרים.
שאלות החימום הן שאלות שלא יקבלו ציון, והן בדרך כלל קלות יותר. אבל כדאי מאוד לוודא שיודעים איך לפתור אותן, אפילו בעל פה.
ציון התרגול יהיה הממוצע של הציונים של תרגילי הבית, אחרי שהוצאנו את שני התרגילים הנמוכים. זה אומר שהציון לא יכול לרדת מהגשה של תרגיל, אלא רק להישאר או לעלות.
חוברת מערכי תרגול
הערה: חשוב לשים לב כי מערכי התרגול לא חופפים לגמרי למה שנלמד בכיתה, ולעתים עלולים להכיל טעויות! נשמח לשמוע הערות והצעות למערכים.
חוברת מערכי תרגול (לפעמים צריך לרענן את הדף כדי לקבל את הגרסה האחרונה, שבה סדר התרגולים יותר מתאים למה שעשינו בכיתה.)
לא מדויק
הבלוג לא מדויק של גדי אלכסנדרוביץ' הוא מקור מצוין למי שחושב שאיבד את הדרך בקורס, וגם למי שלא. רוב הפוסטים שקשורים לקורס מופיעים בקטגוריה אלגברה מופשטת, למשל:
- אז מה זו בעצם חבורה?
- תתי-חבורות וחבורות ציקליות
- קוסטים, משפט לגראנז' וחבורות מנה
- הומומורפיזמים של חבורות
- משפטי האיזומורפיזם של חבורות
- חבורות של תמורות
ויש גם פוסטים על RSA:
