הבדלים בין גרסאות בדף "83-110 לינארית להנדסה תשעד סמסטר א/תרגילים"
מתוך Math-Wiki
אחיה בר-און (שיחה | תרומות) |
אחיה בר-און (שיחה | תרומות) |
||
| (5 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 16: | שורה 16: | ||
*[[מדיה:13LinearEngEx5.pdf|תרגיל 5]] | *[[מדיה:13LinearEngEx5.pdf|תרגיל 5]] | ||
*[[מדיה:13LinearEngsol5.pdf|פתרון תרגיל 5]] | *[[מדיה:13LinearEngsol5.pdf|פתרון תרגיל 5]] | ||
| + | *[[מדיה:13LinearEngEx6.pdf|תרגיל 6]] | ||
| + | *[[מדיה:13LinearEngsol6.pdf|פתרון תרגיל 6]] | ||
| + | *[[מדיה:13LinearEngEx7.pdf|תרגיל 7]] | ||
| + | *[[מדיה:13LinearEngsol7.pdf|פתרון תרגיל 7]] | ||
| + | *[[מדיה:13LinearEngEx8.pdf|תרגיל 8]] | ||
| + | תרגיל נוסף (כלל המקבילית): יהא <math>V</math> ממ"פ, יהיו <math>x,y\in V</math> | ||
| + | הוכיחו כי <math>2(||x||^2+||y||^2)=||x+y||^2+||x-y||^2</math> | ||
| + | |||
| + | הערה: יהא <math>V</math> מרחב נורמי (מרחב וקטורי עם נורמה) שכלל המקבילית מתקיים בו אזי ניתן להגדיר עליו מכפלה פנימית (כלומר כלל המקבילית הוא איפיון אמ"מ לממ"פ). | ||
| + | |||
| + | *[[מדיה:13LinearEngsol8.pdf|פתרון תרגיל 8]] | ||
| + | *[[מדיה:13LinearEngEx9.pdf|תרגיל 9]] | ||
| + | *[[מדיה:13LinearEngsol9.pdf|פתרון תרגיל 9]] | ||
| + | *[[מדיה:13LinearEngEx10.pdf|תרגיל 10]] | ||
| + | *[[מדיה:13LinearEngsol10.pdf|פתרון תרגיל 10]] | ||
| + | *[[מדיה:13LinearEngEx11.pdf|תרגיל 11]] | ||
| + | *[[מדיה:13LinearEngsol11.pdf|פתרון תרגיל 11]] | ||
| + | *תרגיל 12 רובו ככולו בנוי משאלות של חומר שלא למדנו (לכן הדילוג במספור) | ||
| + | *[[מדיה:13LinearEngEx13.pdf|תרגיל 13]] | ||
| + | *[[מדיה:13LinearEngsol13.pdf|פתרון תרגיל 13]] | ||
גרסה אחרונה מ־14:32, 9 בינואר 2014
83-110 לינארית להנדסה תשעד סמסטר א
אפשר להגיע לתרגילי הבית שניתן עליהם ניקוד דרך פה קישור לש.ב. (כמובן, צריך לבחור את הקורס המתאים מתוך הרשימה)
התרגילים שמופיעים פה הם תרגילים נוספים לתירגול ללא ניקוד. כדאי לפתור גם אותם, במיוחד את תרגילי ההוכחה למיניהם (ייתכן מאוד כי חלק מהתרגילים יופיעו בבחנים או במבחן).
- תרגיל 1
- פתרון תרגיל 1
- תרגיל 2
- פתרון תרגיל 2
- תרגיל 3
- פתרון תרגיל 3
- תרגיל 4
- פתרון תרגיל 4
- תרגיל 5
- פתרון תרגיל 5
- תרגיל 6
- פתרון תרגיל 6
- תרגיל 7
- פתרון תרגיל 7
- תרגיל 8
תרגיל נוסף (כלל המקבילית): יהא 
ממ"פ, יהיו 
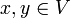הוכיחו כי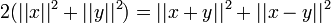 
הערה: יהא מרחב נורמי (מרחב וקטורי עם נורמה) שכלל המקבילית מתקיים בו אזי ניתן להגדיר עליו מכפלה פנימית (כלומר כלל המקבילית הוא איפיון אמ"מ לממ"פ).
- פתרון תרגיל 8
- תרגיל 9
- פתרון תרגיל 9
- תרגיל 10
- פתרון תרגיל 10
- תרגיל 11
- פתרון תרגיל 11
- תרגיל 12 רובו ככולו בנוי משאלות של חומר שלא למדנו (לכן הדילוג במספור)
- תרגיל 13
- פתרון תרגיל 13
