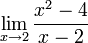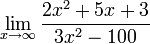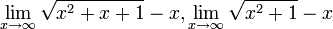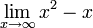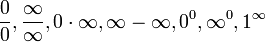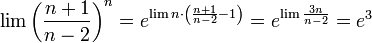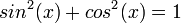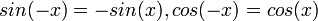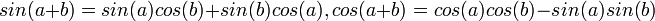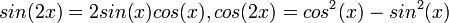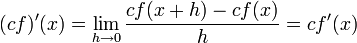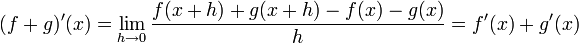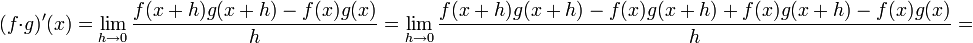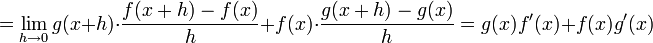83-112 חדו"א 1 להנדסה/נושאי הקורס
מתוך Math-Wiki
תוכן עניינים
- 1 מבחנים מהעבר
- 2 נושאי ההרצאות
- 2.1 הרצאה 1
- 2.2 הרצאה 2
- 2.3 הרצאה 3
- 2.4 הרצאה 4
- 2.5 הרצאה 5
- 2.6 הרצאה 6
- 2.7 הרצאה 7
- 2.8 הרצאה 8
- 2.9 הרצאה 9
- 2.10 הרצאה 10
- 2.11 הרצאה 11
- 2.12 הרצאה 12
- 2.13 הרצאה 13
- 2.14 הרצאה 14
- 2.15 הרצאה 15
- 2.16 הרצאה 16
- 2.17 הרצאה 17
- 2.18 הרצאה 18
- 2.19 הרצאה 19
- 2.20 הרצאה 20
- 2.21 הרצאה 21
- 2.22 הרצאה 22
- 2.23 הרצאה 23
מבחנים מהעבר
- מבחן מועד א תשע"ו
- מבחן מועד ב תשע"ו
- מבחן מועד ג תשע"ו
- מבחן דמה תשע"ו
- מבחן לדוגמה תשע"ו
- מבחן דמה תשע"ז
- מבחן מועד א' תשע"ז
- מבחן מועד ב' תשע"ז
- מבחן מועד ג' תשע"ז
- מבחן דמה תשע"ח
- מבחן מועד א' תשע"ח
- מבחן מועד ב' תשע"ח
- מבחן מועד ג' תשע"ח
- מבחן מועד א' תשע"ט
- מבחן מועד ב' תשע"ט
נושאי ההרצאות
שימו לב: נושאי ההרצאות יעודכנו במהלך הסמסטר לפי קצב ההתקדמות בפועל.
הרצאה 1
- מבוא למספרים - טבעיים, שלמים, רציונאליים, ממשיים.
- שורש 2, 0.999.
- חזקות.
- לוגריתמים.
- מבוא לגבולות (שיטות אלגבריות: כפל בצמוד, הוצאת חזקה משמעותית).
הרצאה 2
- כמתים, שלילת כמתים.
- חסמים.
הרצאה 3
- ברציונאליים אין לכל קבוצה חסומה מלעיל חסם עליון.
- הגדרת הגבול של סדרה במובן הצר.
הרצאה 4
- גבול הוא יחיד.
- נניח בשלילה שיש שני גבולות שונים. החל משלב מסויים כל איברי הסדרה גדולים מאמצע הקטע בין שני הגבולות וגם קטנים ממנו, בסתירה.
- הסדרה הקבועה.
- כל סדרה המתכנסת במובן הצר חסומה.
- אריתמטיקה (חשבון) גבולות.
- (אי שיוויון המשולש.)
- סכום.
- מכפלה.
- חלוקה (תרגיל לבית).
הרצאה 5
- התכנסות במובן הרחב.
- אחד חלקי 'שואפת לאינסוף' היא אפיסה, ההפך לא נכון.
- סנדביץ' וחצי סדנביץ'.
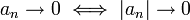
- חסומה כפול אפיסה היא אפיסה.
הרצאה 6
- אינדוקציה.
- ברנולי - אקספוננט חיובי שואף לאפס, אחד או אינסוף.
- אריתמטיקה מורחבת (הכתיב הוא מקוצר ואינו מדוייק):
- חסומה כפול אפיסה = אפיסה
- חסומה חלקי אינסוף = אפיסה
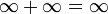
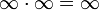
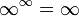
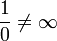
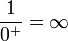
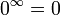
- אינסוף כפול סדרה השואפת למספר חיובי = אינסוף.
- אינסוף כפול סדרההשואפת למספר שלילי = אינסוף.
- יש גבול סופי + אין גבול סופי = אין גבול סופי.
- אינסוף ועוד חסומה שווה אינסוף.
- אם
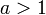 אזי
אזי 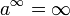
- חזקת סדרות שואפת לחזקת הגבולות.
- המקרים הבעייתיים בהם צריך להפעיל מניפולציות אלגבריות או משפטים על מנת לחשב את הגבול:
- מבחן המנה (אי-שוויון הממוצעים).
- הגבול של השורש הn של n.
הרצאה 7
- סדרה מונוטונית וחסומה מתכנסת.
- המספר e (הוכחות בעזרת אי-שוויון הממוצעים).
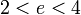 .
.- אם
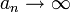 אזי
אזי 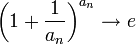
![[a_n]\leq a_n \leq [a_n]+1](/images/math/c/0/9/c095d2afd802a2af89cdf9562a2b2821.png) , כאשר
, כאשר ![[a_n]](/images/math/d/d/d/ddd7e59703916ae1fe3308251c7a0b70.png) הוא המספר השלם הגדול ביותר שקטן או שווה ל
הוא המספר השלם הגדול ביותר שקטן או שווה ל .
.![\left(1+\frac{1}{[a_n]+1}\right)^{[a_n]}\leq\left(1+\frac{1}{a_n}\right)^{a_n}\leq \left(1+\frac{1}{[a_n]}\right)^{[a_n]+1}](/images/math/b/1/0/b10e02f2fc563c7f1153080982e1f8ca.png)
- שני הצדדים שואפים לe ולכן לפי כלל הסנדוויץ הסדרה אכן שואפת לe.
- אם
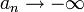 אזי
אזי 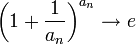
- ראשית
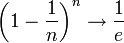 (הוכחה בקישור לערך על המספר e).
(הוכחה בקישור לערך על המספר e). - כעת חזקה שלילית הופכת את השבר, וניתן לסיים את ההוכחה באופן דומה להוכחה במקרה הקודם.
- ראשית
- אם
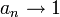 אזי
אזי 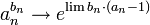
![a_n^{b_n}=\left[\left(1+(a_n-1)\right)^{\frac{1}{a_n-1}}\right]^{ b_n\cdot (a_n-1)}](/images/math/1/b/e/1be3fddf2ca563da0e4e631530a64ce5.png) .
.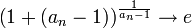 בין אם
בין אם 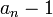 שלילי או חיובי, לפי הטענות לעיל.
שלילי או חיובי, לפי הטענות לעיל.- שימו לב שאם
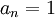 , אז ממילא מקבלים 1 בנוסחא הסופית, ואז לא צריך לחלק ב
, אז ממילא מקבלים 1 בנוסחא הסופית, ואז לא צריך לחלק ב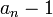 ששווה אפס.
ששווה אפס.
- דוגמא:
הרצאה 8
- פונקציות וגבולות של פונקציות, לפי קושי ולפי היינה.
- תתי סדרות וגבולות חלקיים (ללא הוכחה)
- סדרה מתכנסת לגבול אם"ם הגבול החלקי העליון והתחתון שווים לו.
- אם ניתן לחלק סדרה לתתי סדרות שכולן מתכנסות לאותו גבול, אזי זה גבול הסדרה.
- מסקנה: גבול של פונקציה קיים בנקודה אם"ם הגבולות החד צדדיים קיימים ושווים לו.
הרצאה 9
- הגדרת סינוס וקוסינוס ע"י מעגל היחידה.
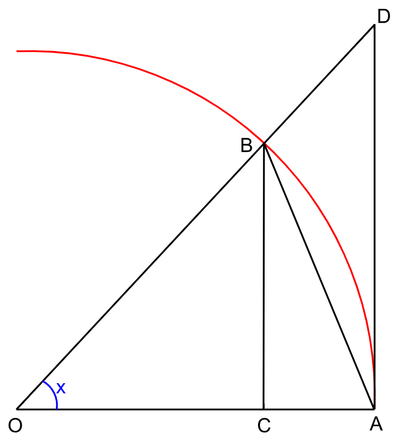
- עבור זוית
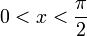 שטח המשולש חסום בשטח הגזרה (משולש פיצה עם הקשה) שחסום בשטח המשולש:
שטח המשולש חסום בשטח הגזרה (משולש פיצה עם הקשה) שחסום בשטח המשולש: 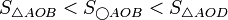
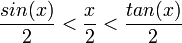
- כיוון ש
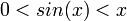 בתחום
בתחום 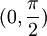 , נובע לפי סנדוויץ' ש
, נובע לפי סנדוויץ' ש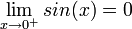 .
. - כיוון שמדובר בפונקציה אי זוגית, נובע שזה גם הגבול משני הצדדים.
- כעת בתחום
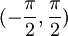 הקוסינוס חיובית ולכן
הקוסינוס חיובית ולכן 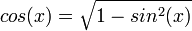 ונובע כי
ונובע כי 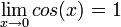 .
.
- כיוון ש
- נחלק את אי השיוויון הטריגונומטרי בסינוס ונקבל:
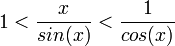
- לפי כלל הסנדביץ
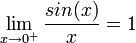
- כיוון שמדובר בפונקציה זוגית, נובע שהגבול משני הצדדים שווה 1.
- עבור זוית
- ראינו ש
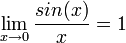 .
. - שימו לב ש
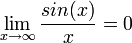 , כיוון שמדובר בחסומה חלקי שואפת לאינסוף.
, כיוון שמדובר בחסומה חלקי שואפת לאינסוף.
הרצאה 10
- גבול של הרכבת פונקציות נכשל ללא רציפות.
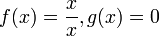 מתקיים כי
מתקיים כי 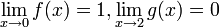 אבל
אבל 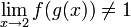 .
.
- רציפות.
- טענה: אם f רציפה ב
 אזי לכל סדרה
אזי לכל סדרה  (גם אם אינה שונה מ
(גם אם אינה שונה מ ) מתקיים כי
) מתקיים כי 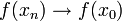 .
. - הרכבת רציפות: תהי f רציפה ב
 ותהי g רציפה ב
ותהי g רציפה ב . אזי
. אזי 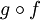 רציפה ב
רציפה ב .
.
- הוכחה:
- תהי סדרה
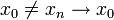 אזי
אזי 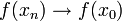
- לפי הטענה הקודמת,
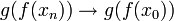 .
.
- מיון אי רציפות.
- רציפות - הגבול בנקודה שווה לערך בנקודה.
- סליקה - הגבול קיים וסופי בנקודה, אך שונה מהערך בנקודה או שהפונקציה אינה מוגדרת בנקודה.
- קפיצתית (מין ראשון) - הגבולות החד צדדיים קיימים סופיים ושונים בנקודה.
- עיקרית (מין שני) - אחד הגבולות החד צדדיים אינו קיים או שאינו סופי.
הרצאה 11
הגדרת הנגזרת
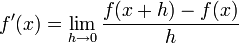
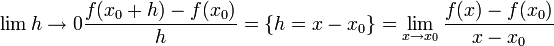
- הסבר לגבי שיטת ההצבה בה השתמשנו לעיל:
- נניח כי
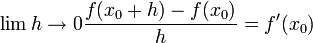 ונוכיח כי
ונוכיח כי 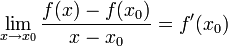 , והוכחה דומה בכיוון ההפוך.
, והוכחה דומה בכיוון ההפוך. - תהי
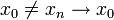 נגדיר את הסדרה
נגדיר את הסדרה 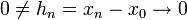 .
. - כיוון ש
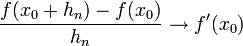 נובע כי
נובע כי 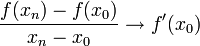 .
.
- אם f גזירה בנקודה, היא רציפה בנקודה:
- צ"ל
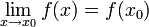
- לפי אריתמטיקה של גבולות זה שקול ל
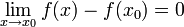
- לפי עקרון win (קיצור של wouldn't it be nice?) מתקיים כי
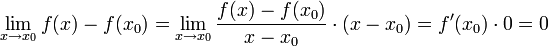
- צ"ל
- פונקציה הערך המוחלט אינה גזירה באפס
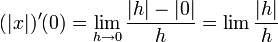 וגבול זה אינו קיים, כיוון שהגבולות החד צדדים שונים.
וגבול זה אינו קיים, כיוון שהגבולות החד צדדים שונים.- ניתן לשים לב גם ש
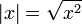 , וכמו כן נראה בהמשך כי
, וכמו כן נראה בהמשך כי אינה גזירה באפס.
אינה גזירה באפס.
הנגזרות של הפונקציות האלמנטריות
- טריגו:
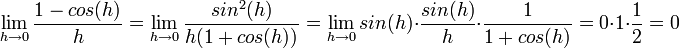
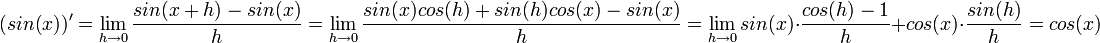
- באופן דומה
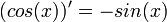
- לוג:
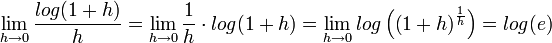
- המעבר האחרון נובע מהעובדה שפונקצית הלוג רציפה.
- (בפרט נובע כי
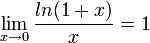 .)
.)
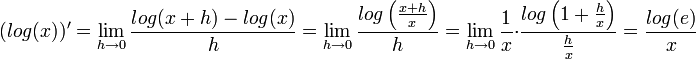
- בפרט נובע כי
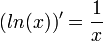
- בפרט נובע כי
- אקספוננט:
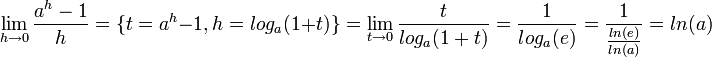
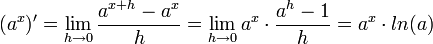
- בפרט נובע כי
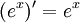 .
.
- בפרט נובע כי
- חזקה:
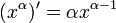 לכל
לכל 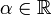 , הוכחה בהמשך.
, הוכחה בהמשך.
- בפרט:
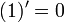
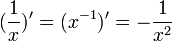
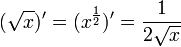
הרצאה 12
נגזרת של מכפלה בקבוע, סכום ומכפלת פונקציות
תהיינה 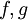 גזירות בנקודה x.
גזירות בנקודה x.
- שימו לב ש
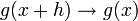 כיוון שg רציפה בx, כיוון שהיא גזירה בx.
כיוון שg רציפה בx, כיוון שהיא גזירה בx.
נגזרת של הרכבה
תהי f גזירה ב ותהי g הגזירה ב
ותהי g הגזירה ב :
:
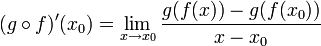
- תהי סדרה
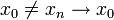 .
. - רוצים לומר ש
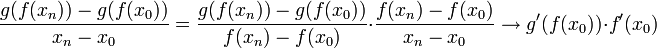 .
. - אמנם
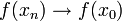 בגלל שהרציפות נובעת מהגזירות, אבל לא ידוע ש
בגלל שהרציפות נובעת מהגזירות, אבל לא ידוע ש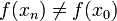 ובמקרה זה אנחנו כופלים ומחלקים באפס.
ובמקרה זה אנחנו כופלים ומחלקים באפס. - אם יש תת סדרה
 של
של 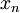 עבורה
עבורה 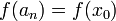 אזי
אזי 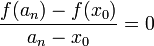 ולכן
ולכן 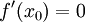 .
. - לכן
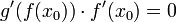 .
. - כמו כן,
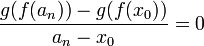 .
. - לכן בכל מקרה קיבלנו כי
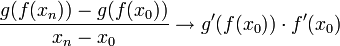
- סה"כ
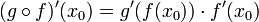 .
.
נגזרת של חזקה
- עבור
 מתקיים
מתקיים 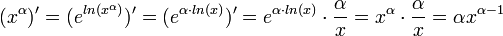
- דוגמא: חישוב הנגזרת של
נגזרת מנה
תהיינה f,g גזירות בנקודה x כך ש 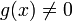 :
:
- נזכור כי
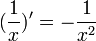
- אזי בנקודה x מתקיים:
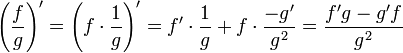
הרצאה 13
- הגדרה:
- פונקציה f נקראית רציפה בקטע
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אם f רציפה בכל נקודה בקטע
אם f רציפה בכל נקודה בקטע  ובנוסף
ובנוסף 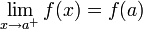 וגם
וגם 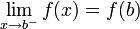
- פונקציות הפיכות (הוכחות והגדרות מדוייקות בבדידה).
- פונקציה
![f:[a,b]\to [c,d]](/images/math/6/a/d/6ad907c775ff05b8176b946ff921b21c.png) הפיכה אם"ם היא חח"ע ועל
הפיכה אם"ם היא חח"ע ועל - הפונקציה ההופכית היא
![f^{-1}:[c,d]\to[a,b]](/images/math/a/0/3/a03dbad0cc5ab3eebe2bba1a2c7bd947.png) ומתקיים כי
ומתקיים כי 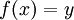 אם"ם
אם"ם 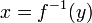
- פונקציה
- טענה: אם
![f:[a,b]\to [c,d]](/images/math/6/a/d/6ad907c775ff05b8176b946ff921b21c.png) רציפה בקטע
רציפה בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , אזי
, אזי ![f^{-1}:[c,d]\to[a,b]](/images/math/a/0/3/a03dbad0cc5ab3eebe2bba1a2c7bd947.png) רציפה בקטע
רציפה בקטע ![[c,d]](/images/math/c/3/1/c31d2b7df15fa7d119c2f8d13f69e10b.png) .
.
- הוכחה:
- תהי
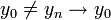 , צ"ל ש
, צ"ל ש 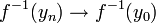
- יהי גבול חלקי
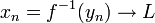 .
. - אזי
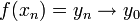 .
. - מצד שני, לפי רציפות הפונקציה f מתקיים
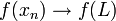 .
. - לכן
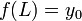 ולכן
ולכן 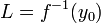 .
.
- טענה: תהי
![f:[a,b]\to [c,d]](/images/math/6/a/d/6ad907c775ff05b8176b946ff921b21c.png) הפיכה גזירה בנק'
הפיכה גזירה בנק' 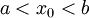 כך ש
כך ש 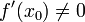 .
.
- אזי
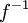 גזירה בנק'
גזירה בנק'  ומתקיים כי
ומתקיים כי 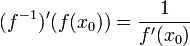 או בנוסח אחר-
או בנוסח אחר-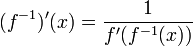
- הוכחה:
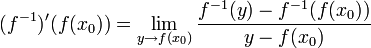
- תהי
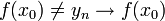 ונסמן
ונסמן 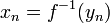 .
. - אזי מתוך רציפות וחח"ע נובע כי
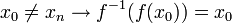
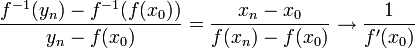
- דוגמא חשובה:
 הפיכה וההופכית שלה נקראית
הפיכה וההופכית שלה נקראית 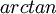 .
.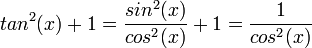
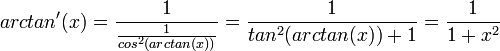
הרצאה 14
- משפט ערך הביניים.
- תהי f רציפה ב
![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) כך ש
כך ש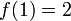 , הוכיחו שקיימת נק'
, הוכיחו שקיימת נק' ![c\in [0,1]](/images/math/6/e/a/6ea0a95f41192a6ad436a6874796e0cb.png) עבורה
עבורה 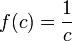
- נעביר אגף ונביט בפונקציה
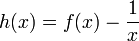 שצריך למצוא שורש שלה.
שצריך למצוא שורש שלה. 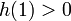 .
.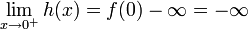 ולכן קיימת נקודה
ולכן קיימת נקודה 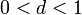 עבורה
עבורה 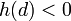 .
.- לפי משפט ערך הביניים בקטע
![[d,1]](/images/math/f/5/d/f5dbfa5a8804773df765ab6203ce1ae4.png) קיימת נק' המאפסת את הפונקציה h.
קיימת נק' המאפסת את הפונקציה h.
- נעביר אגף ונביט בפונקציה
- לכל סדרה יש תת סדרה מונוטונית.
הרצאה 15
- משפטי ויירשטראס.
- פונקציה רציפה בקטע סופי סגור - חסומה.
- פונקציה רציפה בקטע סופי סגור - מקבלת מינימום ומקסימום.
- משפט פרמה.
- אם פונקציה גזירה בנק' קיצון מקומי, הנגזרת שווה שם לאפס.
- ההפך אינו נכון.
- משפט רול.
- פונקציה רציפה בקטע סגור, וגזירה בקטע הפתוח, שמקבלת את אותו ערך בקצוות - הנגזרת שלה מתאפסת בקטע הפתוח.
- לפולינום יש לכל היותר n שורשים שונים.
- משפט לגראנז'.
- פונקציה רציפה בקטע סגור, וגזירה בקטע הפתוח מקבלת את השיפוע בין שתי נקודות הקצה בנגזרת בנק' כלשהי.
- משפט לגראנז' המוכלל.
- שתי פונקציות רציפות בקטע סגור, גזירות בקטע הפתוח, והנגזרת של האחת אינה מתאפסת. אזי מנת הנגזרות שווה למנת השיפועים בנק' מסויימת.
הרצאה 16
- הוכחת משפט לגראנז' המוכלל, שמוכיח גם את משפט לגראנז' עצמו כמקרה פרטי.
- ראשית, כיוון ש
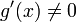 בקטע
בקטע 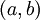 נובע לפי רול כי
נובע לפי רול כי 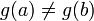 ולכן מותר לחלק בהפרש ביניהם.
ולכן מותר לחלק בהפרש ביניהם. 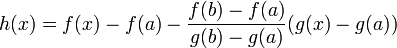
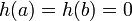 ולכן לפי רול קיימת נק'
ולכן לפי רול קיימת נק' 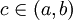 עבורה
עבורה 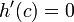 וזה מה שרצינו להוכיח.
וזה מה שרצינו להוכיח.- (שימו לב שמותר לחלק ב
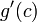 .)
.) - עבור
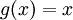 נקבל את משפט לאגראנז' הרגיל.
נקבל את משפט לאגראנז' הרגיל.
- ראשית, כיוון ש
- פונקציה גזירה עולה אם"ם הנגזרת שלה גדולה או שווה אפס.
- פונקציה עולה ממש אם"ם הנגזרת שלה גדולה או שווה אפס, ולא מתאפסת על קטע.
- כלל לופיטל (הוכחה לאפס חלקי אפס בנקודה סופית).
- כיצד להעזר בלופיטל בכל אחד מהמקרים הבעייתיים.
הרצאה 17
- פולינום טיילור.
- שארית לגראנז' בפולינום טיילור.
הרצאה 18
הרצאה 19
- אינטגרל - מסויים ולא מסוים.
- הצגת נוסחאת ניוטון לייבניץ - הוכחה עם הערך הממוצע האינטגרלי.
הרצאה 20
- אינטגרציה בחלקים.
- שיטת ההצבה.
הרצאה 21
- אינטגרל על פונקציה רציונאלית.
הרצאה 22
- סכומי רימן.
- אורך עקומה, נפח גוף סיבוב.
הרצאה 23
- אינטגרלים לא אמיתיים.
- מבחני התכנסות.