הבדלים בין גרסאות בדף "89-113 תשע"ג ב'-תרגילי בית"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏תרגיל 11)
 
(34 גרסאות ביניים של 3 משתמשים אינן מוצגות)
שורה 70: שורה 70:
  
 
[[מדיה:89113solution5.pdf|פתרון]]
 
[[מדיה:89113solution5.pdf|פתרון]]
 +
 +
תיקון לתרגיל 1.ג:
 +
 +
'''חד-חד-ערכיות:
 +
 +
<math>Tv=0 => T(\Sigma \alpha_i v_i)=0 =>\Sigma \alpha_i  T(v_i)=0 => \forall i\ \alpha_i=0 => v=0 => ker(T)=0</math>
 +
 +
'''על:
 +
 +
נגדיר: <math>\forall i\ T(v_i)=b_i</math>
 +
 +
אזי:
 +
 +
<math>\forall w\in W \exists \alpha_1,...,\alpha_n:w=\Sigma\alpha_i b_i, \forall i \exists v_i: T(v_i)=b_i => \forall w\in W\exists v=\Sigma\alpha_i v_i\in V: w=\Sigma\alpha_i b_i=\Sigma\alpha_i T(v_i)= T(\Sigma\alpha_i v_i)=T(v)</math>
  
 
==תרגיל 6==
 
==תרגיל 6==
שורה 85: שורה 99:
  
  
−
[[מדיה:89113solution6.pdf|פתרון]]
+
[[מדיה:89113sol6.pdf|פתרון]]
  
 
==תרגיל 7==
 
==תרגיל 7==
שורה 96: שורה 110:
 
[[מדיה:89113_ex7.pdf‏|תרגיל 7]]
 
[[מדיה:89113_ex7.pdf‏|תרגיל 7]]
  
−
[[מדיה:89113solution7.pdf|פתרון]]
+
[[מדיה:89113_ex7_sol.pdf|פתרון]]
  
 
==תרגיל 8==
 
==תרגיל 8==
שורה 107: שורה 121:
 
[[מדיה:89113_ex8.pdf‏|תרגיל 8]]
 
[[מדיה:89113_ex8.pdf‏|תרגיל 8]]
  
−
[[מדיה:89113solution8.pdf|פתרון]]
+
[[מדיה:89113solution8.doc|פתרון]]
  
 
==תרגיל 9==
 
==תרגיל 9==
 
להגשה ב-
 
להגשה ב-
  
−
הקבוצות של עידן: יפורסם בהמשך
+
הקבוצות של עידן: 6/6
  
 
הקבוצות של עדי ניב ויפית/עדי לוגסי: 26/5
 
הקבוצות של עדי ניב ויפית/עדי לוגסי: 26/5
שורה 121: שורה 135:
  
 
==תרגיל 10==
 
==תרגיל 10==
 +
'''עדכון: שאלה 4 היא שאלת בונוס בשווי 15 נק'.'''
 +
 +
'''רמזים:
 +
 +
שאלה 3 - שימו לב שצריך לבחור <math>\alpha \ne 0</math> מסויים כדי לקבל תלות לינארית.
 +
 +
שאלה 4 - ההגדרה של מטריצה אוניטרית בתוך הסוגריים היא ההגדרה הכללית לממ"פ מעל  <math>\mathbb{R}</math>  או מעל  <math>\mathbb{C}</math>. ההגדרה מחוץ לסוגריים מתאימה למקרה <math>\mathbb{F}=\mathbb{R}</math>.
 +
 +
שאלה 4 - זכרו שוקטור הקוארדינטות לפי בסיס אורתונורמלי הוא וקטור המ"פ עם איברי הבסיס. כדאי גם להיזכר בשוויון פרסבל.
 +
 +
'''
 +
 +
'''תיקון: בשאלה 6 מדובר במרחב הפולינומים <math>R_2[x]</math>'''
 +
 
להגשה ב-
 
להגשה ב-
  
−
הקבוצות של עידן: יפורסם בהמשך
+
הקבוצות של עידן: 13/6
  
−
הקבוצות של עדי ניב ויפית/עדי לוגסי: 2/6
+
הקבוצות של עדי ניב ויפית/עדי לוגסי: 9/6
  
 
[[מדיה:89113ex10.pdf‏|תרגיל 10]]
 
[[מדיה:89113ex10.pdf‏|תרגיל 10]]
  
−
[[מדיה:89113solution10.pdf|פתרון]]
+
[[מדיה:89113_ex10_sol.pdf|פתרון]]
 +
 
 +
==תרגיל 11==
 +
שימו לב: יש שאלת בונוס!!
 +
בפתרון יש קצת בלבול בין מספר השאלה לפתרון שלה. פתרון שאלה 4 מופיע ב6 . 5 ב 4 , 6 ב5.
 +
 
 +
להגשה ב-
 +
 
 +
הקבוצות של עידן: 20/6
 +
 
 +
הקבוצות של עדי ניב ויפית/עדי לוגסי: 16/6
 +
 
 +
[[מדיה:89113exe11.pdf‏|תרגיל 11]]
 +
 
 +
[[מדיה:89113solution11.pdf|פתרון]]
 +
 
 +
[[מדיה:89113targil10correction.pdf|שאלה 6 - תיקון]]
 +
 
 +
==תרגיל 12==
 +
 
 +
לא להגשה
 +
 
 +
[[מדיה:89113exe12.doc|תרגיל 12]]
 +
 
 +
שאלה 3.12 היא בהמשך לתרגיל 3.10, ולא 3.9 כפי שמופיע.
 +
 
 +
[[מדיה:89113_ex12_sol.pdf|פתרון]]
 +
 
 +
==תרגיל 13==
 +
 
 +
לא להגשה
 +
 
 +
[[מדיה:89113tirgul13.pdf|תירגול אחרון]]
 +
 
 +
[[מדיה:89113exe13.pdf|תרגיל 13]]
 +
 
 +
[[מדיה:89113solution13.pdf|פתרון]]

גרסה אחרונה מ־16:05, 5 ביולי 2013

תרגיל 1

תרגיל 1


שימו לב להגדרה המתוקנת של מטריצת ונדרמונדה.

להגשה ב-

הקבוצות של עידן: 13-14/3

הקבוצות של עדי ויפית: 17/3

פתרון

תרגיל 2

להגשה ב-

הקבוצות של עידן: 3-4/4

הקבוצות של עדי ויפית: 7/4

תרגיל 2

פתרון

תרגיל 3

להגשה ב-

הקבוצות של עידן: 10-11/4

הקבוצות של עדי ויפית: 14/4

תרגיל 3

  • 4/4-בוצע תיקון קל בסוף תרגיל 5
  • שימו לב להבדל בין [T]_B, שהיא מטריצה מייצגת עבור ה"ל T מהבסיס B לעצמו, לבין [T(v)]_B שהוא וקטור הקואורדינטות של וקטור מהטווח לפי בסיס הטווח B.

פתרון

תרגיל 4

להגשה ב-

הקבוצות של עידן: 17-18/4

הקבוצות של עדי ניב ויפית/עדי לוגסי: 21/4

תרגיל 4

  • אופרטור=פעולה/פונקציה מקבוצה לעצמה
  • אופרטור הגזירה=פעולה על פונקציה (בשאלה 2 על פולינום) המחזירה את הניגזרת של הפונקציה T(f)=f'.

פתרון

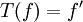תרגיל 5

להגשה ב-

הקבוצות של עידן: 24-25/4

הקבוצות של עדי ניב ויפית/עדי לוגסי: 28/4

תרגיל 5

*שימו לב, כש-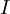I מפיע כה"ל הכוונה להעתקת הזהות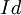 Id

פתרון

תיקון לתרגיל 1.ג:

חד-חד-ערכיות:

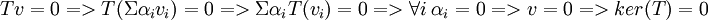
Tv=0 => T(\Sigma \alpha_i v_i)=0 =>\Sigma \alpha_i T(v_i)=0 => \forall i\ \alpha_i=0 => v=0 => ker(T)=0

על:

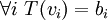
נגדיר: \forall i\ T(v_i)=b_i

אזי:

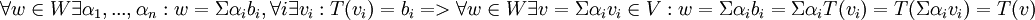
\forall w\in W \exists \alpha_1,...,\alpha_n:w=\Sigma\alpha_i b_i, \forall i \exists v_i: T(v_i)=b_i => \forall w\in W\exists v=\Sigma\alpha_i v_i\in V: w=\Sigma\alpha_i b_i=\Sigma\alpha_i T(v_i)= T(\Sigma\alpha_i v_i)=T(v)

תרגיל 6

להגשה ב-

הקבוצות של עידן: 1-2/5

הקבוצות של עדי ניב ויפית/עדי לוגסי: 5/5

תרגיל 6

  • בשאלה הראשונה אין צורך למצוא פולינום מינימלי.


פתרון

תרגיל 7

להגשה ב-

הקבוצות של עידן: 8-9/5

הקבוצות של עדי ניב ויפית/עדי לוגסי: 12/5

תרגיל 7

פתרון

תרגיל 8

להגשה ב-

הקבוצות של עידן: 19/5

הקבוצות של עדי ניב ויפית/עדי לוגסי: 19/5

תרגיל 8

פתרון

תרגיל 9

להגשה ב-

הקבוצות של עידן: 6/6

הקבוצות של עדי ניב ויפית/עדי לוגסי: 26/5

תרגיל 9

פתרון

תרגיל 10

עדכון: שאלה 4 היא שאלת בונוס בשווי 15 נק'.

רמזים:

שאלה 3 - שימו לב שצריך לבחור 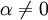\alpha \ne 0 מסויים כדי לקבל תלות לינארית.

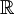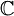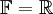שאלה 4 - ההגדרה של מטריצה אוניטרית בתוך הסוגריים היא ההגדרה הכללית לממ"פ מעל \mathbb{R} או מעל \mathbb{C}. ההגדרה מחוץ לסוגריים מתאימה למקרה \mathbb{F}=\mathbb{R}.

שאלה 4 - זכרו שוקטור הקוארדינטות לפי בסיס אורתונורמלי הוא וקטור המ"פ עם איברי הבסיס. כדאי גם להיזכר בשוויון פרסבל.

תיקון: בשאלה 6 מדובר במרחב הפולינומים R_2[x]

להגשה ב-

הקבוצות של עידן: 13/6

הקבוצות של עדי ניב ויפית/עדי לוגסי: 9/6

תרגיל 10

פתרון

תרגיל 11

שימו לב: יש שאלת בונוס!! בפתרון יש קצת בלבול בין מספר השאלה לפתרון שלה. פתרון שאלה 4 מופיע ב6 . 5 ב 4 , 6 ב5.

להגשה ב-

הקבוצות של עידן: 20/6

הקבוצות של עדי ניב ויפית/עדי לוגסי: 16/6

תרגיל 11

פתרון

שאלה 6 - תיקון

תרגיל 12

לא להגשה

תרגיל 12

שאלה 3.12 היא בהמשך לתרגיל 3.10, ולא 3.9 כפי שמופיע.

פתרון

תרגיל 13

לא להגשה

תירגול אחרון

תרגיל 13

פתרון

מקור: https://math-wiki.com/index.php?title=89-113_תשע%22ג_ב%27-תרגילי_בית&oldid=35367